设计数学实验提升课堂活力

2019-07-23杨基娜

数学学习与研究 2019年11期

杨基娜

【摘要】数学是一门系统而严谨的科学，数学活动更多的是思维层面的活动.当前的教育时间紧任务重，数学教学多侧重于逻辑推导，而忽视了观察、实验、操作在学习中的重要作用.数学实验的教学旨在让学生经历自主操作和探究的过程，更好地掌握数学知识，感悟数学方法.

【关键词】数學实验;探究式教学;自主体验

数学教育家G·波利亚曾经指出：“数学有两个侧面，一方面，数学是一门系统的演绎科学，另一方面，数学也是一门试验性的归纳科学.”在实际教学中必须重视学生数学认知结构的形成，为学生提供充分从事数学活动的机会，让学生经历实践，操作的过程，感悟数学知识，提炼数学方法，完善知识结构.

我们把与学生数学认知结构形成有关的教学实践活动称为数学实验.数学实验教学注重学生的主体参与性，让学生从操作中获得数学探究的方法，拓展学生的思维.我们要根据学生的知识储备以及教学目标设计适当的数学实验.针对不同知识类型，数学实验大致分为实物验证型实验、思维验证型实验、技术验证型实验三大类.

一、实物验证型实验，有助于激发学生兴趣

教师在设计数学实验时应基于学生的认识水平，以实际生活经验为依据.例如，学习三角形三边关系，我们可以这样问：是不是任意给定三条线段都可以组成三角形呢？用一根长长的教鞭和两只粉笔可以组成三角形吗？可以准备一些长度不等的木棒让学生分组实验，记录数据.观察数据，要组成一个三角形，边长要满足什么关系呢？在教师的引导下大部分同学都会总结得出“三角形任何两边之和大于第三边”的结论.教师还要从“两点之间线段最短”入手，找到它的理论依据.

在学习“数轴”时，教师可提前让学生观察温度计，用木棒制作一支温度计，课上，让学生观察自制温度计有无做的不正确或不完善的地方，并加以提问：（1）温度计和刻度尺有什么相似的地方？又有哪些不同之处？（2）负数又是按照怎样的顺序标记的呢？（3）我们能不能把温度计上的刻度标的更多一点？通过学生的操作和观察，这些问题都能够答出来，引导学生将这支温度计抽象成一条向两端无限延伸的数轴，从而引出新课.

这样的导入结合了学生的生活经验，从实例中体会到数轴的形象，也让学生更好地理解了数轴的三要素，为学生画数轴以及下一节有理数比较大小扫清了理解上的障碍.

二、操作验证型实验，在操作中感悟知识

操作性实验教学的一般步骤是：提出问题→实验操作→观察分析→假设猜想→交流验证→理论证明.操作性实验教学强调学生的主动参与和自主探究.

初二的中心对称图形一直是学习的重点和难点.借助数学实验，在学习矩形的时候，可以利用现成的矩形让学生动手操作：（1）画出矩形的两条对角线，并量一量，两条对角线有什么关系;（2）把一个矩形沿着两条对角线剪开，形成的四个三角形是什么形状？矩形与平行四边形相比有什么特殊的性质？你能给予证明吗？又如，在学习菱形时，我们根据菱形的定义在平行四边形的基础上剪裁使得邻边相等，画出对角线，沿着对角线折叠你们发现了什么？让学生分组讨论，总结，并给予证明.

通过学生自主经历动手操作的过程，加深对特殊四边形性质的理解，对探究得出的结论的理解也更加深刻.在此过程中，学生真正地成为他们学习上的“主人”，学生的思维得到最大限度的发展，更真切地理解性质，对运用性质作图和解题都有很好的促进作用.

三、巧借几何画板，进行技术验证型实验

开展初中数学实验教学的方法有许多，特别是计算机技术和数学教学软件引入后，数学实验教学的手段更为丰富了.利用几何画板所做的数学实验，将教师从传统的教学模式中解放出来.

初中数学的几何入门，讲点动成线，线动成面，面动成体，单靠想象是无法形成认识的，借助几何画板设计教学课件，让数学教学更加生动形象，让实验教学变得更具有操作性和有效性.通过几何画板的操作，让图形动起来，从而达到举一反三，拓展思维的作用，下面以一道经典的几何实验教学为例：

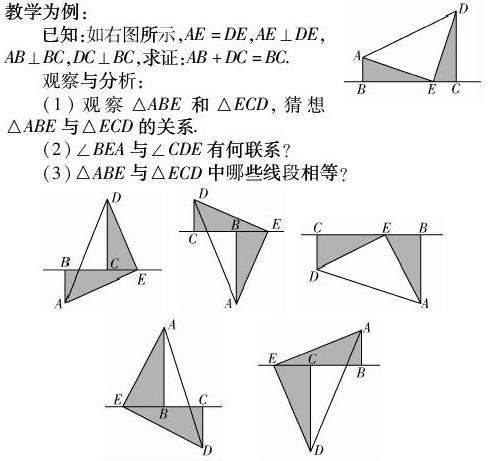
已知：如右图所示，AE=DE，AE⊥DE，AB⊥BC，DC⊥BC，求证：AB+DC=BC.

观察与分析：

（1）观察△ABE和△ECD，猜想△ABE与△ECD的关系.

（2）∠BEA与∠CDE有何联系？

（3）△ABE与△ECD中哪些线段相等？

此道例题是学生学习中常见的基本模型，几何画板的引入为一些抽象的性质和概念的理解提供了直观形象的良好载体.借助于几何画板移动点A的位置，分别得到以上几幅图形，直观展示了线段AB，BC，DC之间的关系.通过这样的设计就变成了动态几何的问题，启发学生的思考，拓展思维.

我们一线教师需要不断思考和改进教学方式，设计多样化的数学实验，优化课堂教学.将静态的数学知识以动态的方式呈现出来，让学生在自主操作中不断发展思维，完善数学知识结构.

【参考文献】