一种水文时间序列异常模式检测方法研究
2019-07-23李云霞姚建国万定生
李云霞,姚建国,万定生,赵 群
(1.河海大学 计算机与信息学院,江苏 南京 211100;2.淮河水利委员会水文局,安徽 蚌埠 233001)
0 引 言
时间序列数据是一种序列值按照时间发生先后顺序排列的特殊数据,在时间序列大量的数据中,有些极个别的子序列与其他子序列有着明显的不同,这些子序列称为异常模式。近年来,异常检测占据着非常重要的地位,受到了越来越多的关注。然而直接在原始时间序列上进行异常检测效率低、可靠性差,因此时间序列表示是必要的。常用的时间序列表示法主要有符号化表示法、频域表示法[1]、奇异值表示法[2]、分段线性表示法[3]。Obuchowski在文献[1]中通过傅里叶变换,将时间序列从时域映射到频域,但傅里叶变换会平滑掉有重要特征的点,对非平稳的时间序列不适用。奇异值表示法将时间序列看成一个矩阵,利用Karhune-Loeve技术实现高维时间序列向低维数据的转化,缺点是奇异值表示法的时空复杂度高。分段线性表示法通过首尾相连的线段将时间序列分割成多个子序列,具有良好的数据压缩和噪声过滤的作用,是使用较多的时间序列数据表示方法之一。
异常检测方法大致分为四类:基于统计的方法[4]、基于距离的方法[5]、基于密度的方法[6-7]和基于聚类的方法[8]等。
1 水文时间序列异常检测方法
根据水文时间序列具有的高维性、海量性等特征,提出一种两阶段的水文时间序列异常检测方法,该方法主要包括三个步骤:时间序列分段线性表示、层次聚类、异常模式检测。文献[9]也采用了两阶段异常检测方法,但其方法与文中方法相差很大,文中方法在异常检测前对时间序列进行分段线性表示,且两阶段检测方法中的聚类方法以及判定异常的方法都不同。
1.1 时间序列分段线性表示
给定长度为n的时间序列t=(t1,t2,…,tn),对时间序列进行等长分割,然后用子序列的极值差、斜率、均值表示这段子序列[10],其中子序列的极值差是子序列中各特征值的最大值和最小值的差值,利用极值差可以表示子序列的起伏程度大小,可以判断这段序列是否平稳;斜率是子序列的实际斜率,可以很好地表现分段子序列的变化趋势;均值是每段子序列的均值,能代表子序列值的一般水平,描述子序列值的集中程度。所以用这三个值能准确地表示子序列的特征。异常检测将用极值差、斜率、均值表示的子序列进行计算,由于三个特征值的值域差别很大,因此要对三者的值域进行规范化。
设t1=(t11,t12,…,t1n)为一个子序列,则利用式1将该组特征值规范到0至1之间。
(1)
其中,tmax和tmin分别表示子序列每个特征值的最大值和最小值。
算法1:时间序列分段线性表示算法。
输入:时间序列(t1,t2,…,tn),子序列长度l;
输出:规范化的子序列。
Step1:将时间序列按长度l进行分段,设m=n/l。
t={t1(t1,t2,…,tl),t2(tl+1,tl+2,…,t2l),…,tm(tn-l,tn-l+1,…,tn)}
Step2:计算子序列的极值差、斜率、均值。
for(i=1 tom){
avgi=sum(ti)/len(ti)
xlvi=(tin-ti(n-1))/len(ti)
edi=timax-timin}
Step3:输出规范化的子序列。
t={(ed1,xlv1,avg1),(ed2,xlv2,avg2),…,(edm,xlvm,avgm)}
1.2 层次聚类
在对时间序列进行分段线性表示之后进行层次聚类,层次聚类方法包括凝聚的层次聚类和分裂的层次聚类[11-12]。凝聚的层次聚类是自底向上形成的,这种方法最初将每个对象作为一个簇,然后这些簇寻找距离最近的簇进行合并,不断重复,直至达到定义的簇的数目。
分裂的层次聚类是自顶向下形成的,这种方法首先将所有对象看成一个簇,然后逐步分为一个个小簇,直到达到某个结束条件。层次聚类具有可以发现类的层次关系,不需要预先制定聚类数,距离和规则的相似度容易定义,限制少等优点。文中采用凝聚的层次聚类方法进行实验。
流程如下:
输入:t={(ed1,xlv1,avg1),(ed2,xlv2,avg2),…,(edm,xlvm,avgm)};
输出:类簇C1,C2,…,Ci。
Step1:将每个对象看作一个初始簇;
Repeat:
Step2:计算两两类之间的距离,找到距离最小的两个类簇C1和C2;
Step3:合并C1和C2为一个新类;
Until:达到定义的簇的数目。
1.3 异常模式检测
异常检测是在类与类之间距离的基础上算出异常因子,通过判断异常因子是否超过给定的阈值来判断模式是否异常,因为异常因子OF(Cj)度量了Cj与其他类之间的距离,距离越大,说明该类与整个数据集的差异程度越大,从而说明该模式异常。其中,在较短时间内某站流量数据突然暴涨或突然下降的事件认定为异常事件,可用于验证检测结果是否准确。
算法2:异常模式检测。
输入:C1,C2,…,Ci,d;
输出:异常模式。
Step1:计算类与类之间的距离[13],设Ci的质心为p=(xp,yp,zp),Cj的质心为q=(xq,yq,zq)。
(2)
Step2:计算异常因子。
(3)
Step3:判定异常模式。
if(OF(Cj)≥d){
输出Cj}
2 实验及结果分析
2.1 实验结果
选取山西省龙门站2002年1月1日至2016年12月31日共15年的汛期小时流量数据作为实验数据,共7 892条。原始时间序列如图1所示。
分别用文中提出的异常检测方法和相关性分析的检测方法[14-15]对龙门站的数据进行检测,通过多次实验发现,相关性分析的方法当e1=0.6,e2=0.03时检测结果最好,检测结果如表1所示。
比较表1可以看出,两种方法都检测出五个异常模式,但是其中有两个异常模式是不同的,为了证明检测的正确性,分别将检测出来的异常模式单独画图,验证其是否异常。图2中的(a)至(f)表示两种方法检测出来的异常模式。
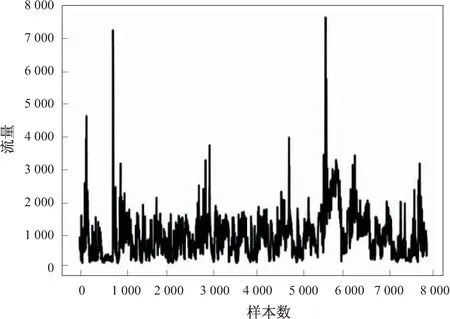
图1 龙门站2002-2016年汛期流量数据时间序列
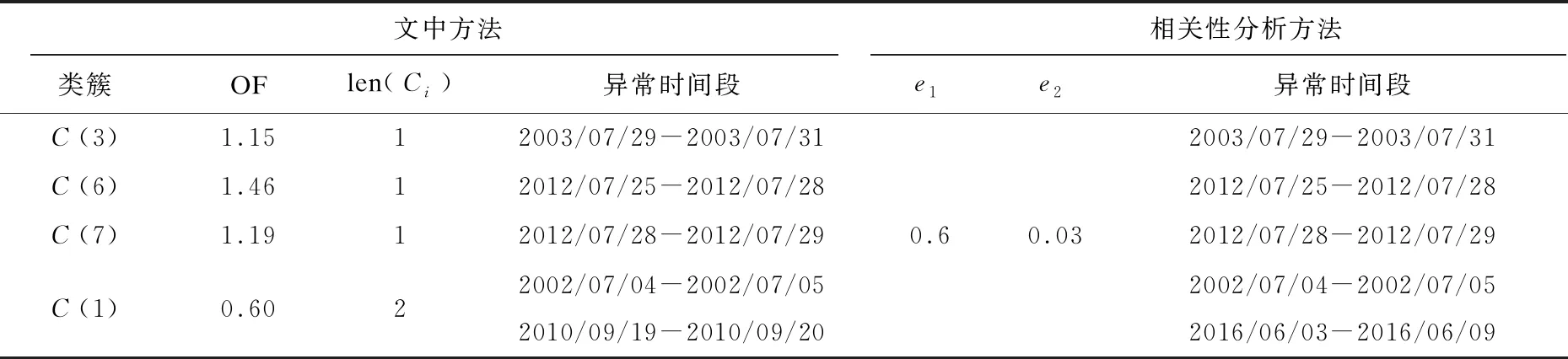
表1 文中方法与相关性分析方法实验结果对照(实测数据)
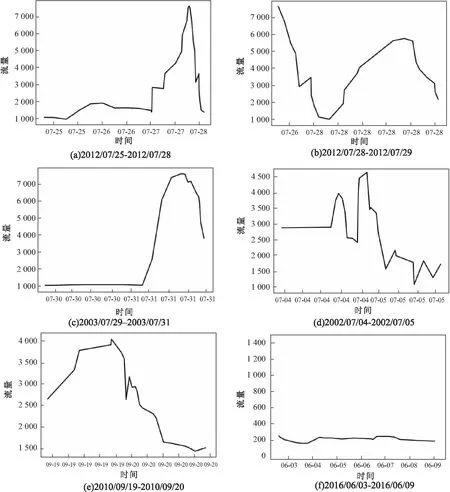
图2 异常序列(1)
利用人工合成数据进行实验,其中人工合成数据是在原始数据的基础上增加了三个异常模式,增加的三个异常模式分别为2005年6月13日至2005年6月21日、2014年9月12日至2014年9月16日、2009年7月18日至2009年7月28日,人工合成数据时间序列如图3所示。
分别用文中的异常检测方法和相关性分析的检测方法进行实验,通过多次实验发现,相关性分析的方法当e1=0.6,e2=0.03时检测结果最好,检测结果如表2所示。
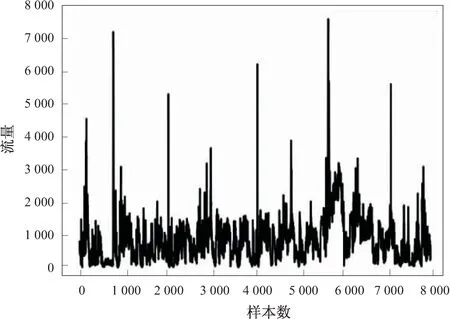
图3 人工合成数据时间序列
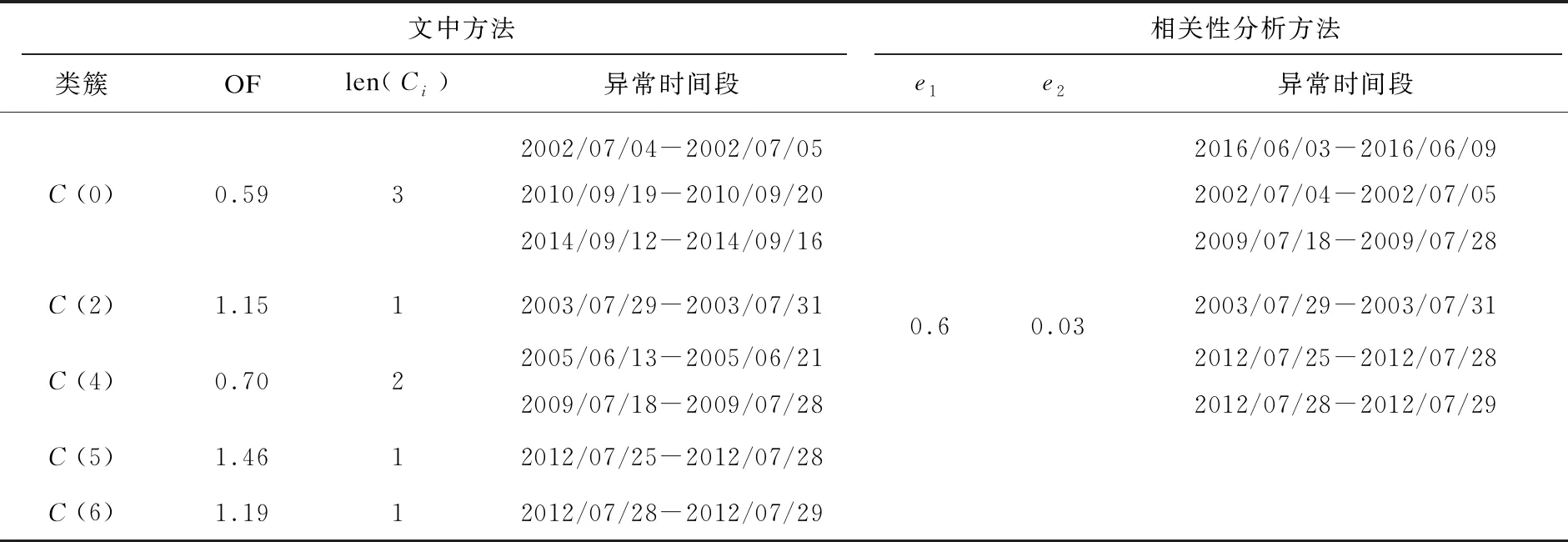
表2 文中方法与相关性分析方法实验结果对照(合成数据)
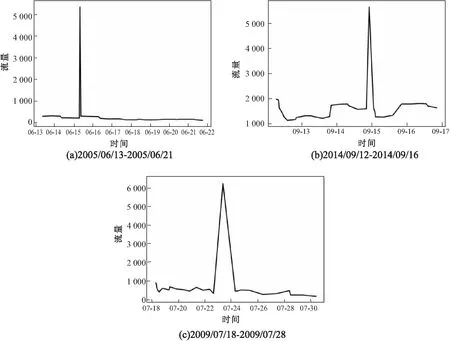
图4 异常序列(2)
2.2 实验分析
通过实验表明,用实测数据进行实验时,文中方法检测出来的五个异常模式,从图2(a)~(e)可以看出该站的流量突然暴涨或者突然下降,这与该站的流量模式不符合,故判定其为异常模式,但相关性分析的检测方法没有检测出2010年9月19日至2010年9月20日这段序列存在异常,从图2(e)可以看出,该段序列的流量快速上升又快速下降,属于异常模式;图2(f)表示2016年6月3日至2016年6月9日这段序列,在该序列中该站流量基本保持不变,不属于异常模式。用人工合成的数据进行实验时,文中方法检测出八个异常模式,从图2(a)~(e)和图4(a)~(c)可以看出这八个模式均属于异常模式,其中图4(a)~(c)的异常模式与人工增加的异常模式吻合,相关性分析的方法只检测出六个异常模式,其中人工合成的三个异常模式,该方法只检测出一个,所以文中的异常检测方法要优于相关性分析的方法。
3 结束语
文中提出一种两阶段的水文时间序列异常检测方法。该方法通过分段线性表示、层次聚类、异常模式检测三个步骤来检测时间序列中存在的异常模式。为验证该算法的准确性,采用另一种相关性分析的异常检测方法进行对比,通过实验发现,文中方法能准确检测出异常模式,而且要优于相关性分析的检测方法。但文中方法利用阈值确定异常模式,使得该阈值对检测结果有一定影响,阈值的确定方式缺少灵活性,有待进一步改进。
