基于Canny算子的C-V水平集模型

喻建锋，吕毅斌，房巾莉，王樱子

(1.昆明理工大学 理学院，云南 昆明 650500；2.昆明理工大学 计算中心，云南 昆明 650500)

0 引 言

图像分割，即把想研究的目标从图像中分割出来，得到相对应的边界。在临床诊断、病理分析、手术计划和影像处理等实践领域有着广泛的研究和应用价值。但是由于图像格式不同、解剖结构复杂和图像边缘不清晰等因素，实现图像分割还是有很多问题。当下，还找不到一种统一的方法能够解决不同的医学图像分割问题，许多国内外学者就各自遇到的种种问题，提出了许多不同的分割方法：基于阈值的分割方法[1-2]、基于区域的分割方法[3-5]、基于边界的分割方法[6-7]和基于某种特定理论的分割方法[8-9]。

Osher和Sethian[10]在1988年得出的水平集算法，是将二维闭合曲线的演化问题转变为三维空间曲面演化的水平集函数的隐含方式来求解，这种分割方法计算出的结果较稳定，所以在图像分割领域，这种方法被广泛采用。

Chan和Vese[11]将水平集方法和Mumford-Shah[12]模型进行结合，得出了C-V水平集模型，这个模型充分利用了图像的全局信息，所以得到的分割结果也较为精确。

但这个模型在求解时所需迭代次数过多。因此，李俊等[13]提出了对水平集方法鲁棒初始化的双向快速步进法，李传龙[14]提出的窄带快速区域水平集C-V模型图像分割方法，都大大减少了计算量。

文中提出一种基于Canny算子的C-V水平集模型，并应用于医学图像的目标分割。通过对原始图像进行预处理，使图像边界信息更加明确，再利用C-V水平集算法得到更好的分割效果，提高了分割性能。

1 水平集算法

水平集算法(level set method)是Osher和Sethian等在1988年提出来的一种几何变形模型。该模型可用来处理复杂的几何体，能应对图形在变化过程中的拓扑结构变化。可以表明水平集模型是一种有效的随时间变化的物体建模方法。

定义函数φ(x,t) (t表示时间)，若φ(x,t) =0时，该函数就能表示出运动的分界面Γ，而x=x(x1,x2,…,xn)∈Rn，所以Level Set方程φ具有以下性质：

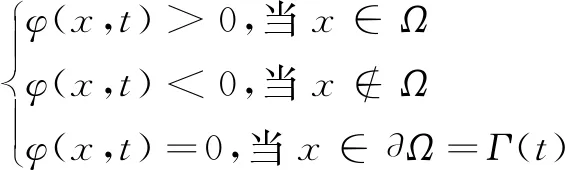
(1)

在任意时间下，边界Γ(t)的位置都可以由φ(x,t) =0得到，且φ(x,t) 满足偏微分方程。

即：

(2)

2 C-V水平集模型

C-V水平集模型不需要图像局部梯度信息，它是利用最小化能量函数来得出图像轮廓曲线。一条闭合的边界C将Ω的原始图像I(x,y)划分成目标、背景2个区域C1,C2，且C1,C2分别为两个区域的平均灰度。能量函数定义为：

E(C,C1,C2)=μLength(C)+

(3)

其中，Length(C)是闭合轮廓线C的长度；μ≥0,λ1,λ2>0是对应各能量项下的权重系数。

若闭合轮廓线不在两个区域的边界上时，E(C,C1,C2)达不到最小值；反之E(C,C1,C2)可取最小值。继续把式3进行优化，就可得出未知数C1,C2及最终的轮廓线C的位置。

即：

(4)

C-V水平集模型前提是图像要分片光滑，为了将E(C,C1,C2)规范化，引入Heavisirle函数H(z)和Dirac函数δ(z)。使用水平集函数φ的零水平集φ=0来表示C，Heavisirle函数H(z)用来划分演化区域，Dirac函数δ(z)用来限定演化的取值必须在零水平集函数的周围，则：

Length(C)=Length(φ=0)=

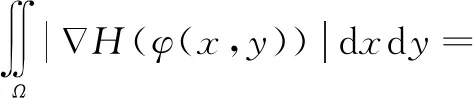
(5)

(6)

(7)

所以，能量函数改写成：

E(φ,C1C2)=

(8)

待分割图像I(x,y)的水平集函数可写成：

I(x,y)=C1H(φ(x,y))+C2(1-H(φ(x,y)))

(9)

利用欧拉-拉格朗日法对式8进行求解，可得到用水平集函数φ表示的偏微分方程[15]：

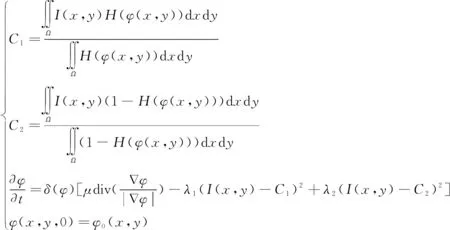
(10)

3 基于Canny算子的C-V水平集算法

3.1 Canny算子

Canny算子应用在图像上是针对图像的一维边缘，对阶跃型边界的检测模板形状与高斯函数的一阶导数类似。

利用二维高斯函数的圆对称性和可分解性，很容易计算出任意方向上的高斯函数方向导数与图像的卷积。所以，选取高斯函数的一阶导数作为阶跃边缘的次最优检测算子来进行边缘检测[16-17]。二维高斯函数数学表达式为：

(11)

原图像为I(x,y)，经过高斯平滑后的图像为：

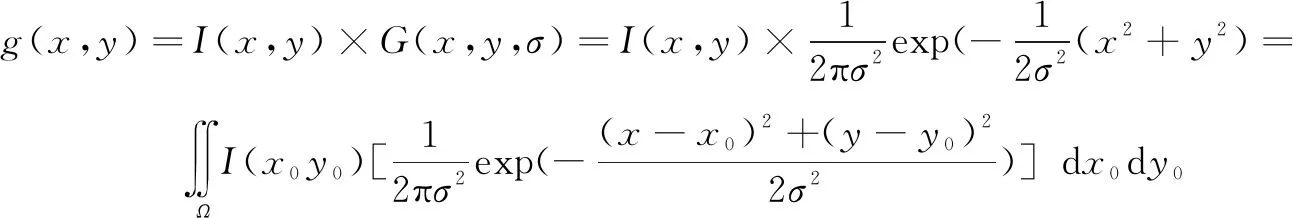
(12)

对平滑后的图像求一阶导数，并将结果写成梯度矢量的形式：

(13)

其中，Gx(x,y,σ)，Gy(x,y,σ)是一阶偏导数。

(14)

3.2 Canny算子和C-V水平集算法的结合及其解析表达

用Canny算子处理结果gxy(x,y)来代替曲线平面(x,y)，则水平集函数φ的零水平集φ=0改写为φ(gxy(x,y))，再用经过高斯平滑后的图像g(x,y)代替传统的C-V水平集算法中的原图I(x,y)，将替换后的解析式代入式3可以得到新的能量函数。

即：

E(C,C1C2)=μLength(C)+λ1

(15)

利用上文的分析和求解，可以得到一个新的用水平集函数φ表示的偏微分方程：

(16)

Canny算子用在图像分割上，充分降低了噪声影响对分割的精度，并将原图用Canny算子处理后的结果来代替，使边缘信息更加明确，分割所得到的结果也就更加精确。

4 数值实验

利用该模型进行医学图像分割，实际上就是要求出式16中偏微分方程的解φ，再取它的零水平集就是所要的分割结果。下面将式16中的偏微分方程转化为差分形式。

(17)

则式16中的偏微分方程可以离散成：

(18)

(19)

为了验证改进算法的有效性，实验采用人体三个不同器官的CT图像来进行分割处理，参数选取为：λ1=λ2=1，轮廓长度系数μ=0.01×255×255，时间步长Δt=1，像素间距h=1，标准偏差σ=0.2，分割结果如图1～图3所示。

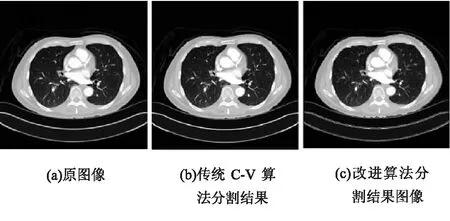
图1 肺部CT图像在不同算法下的分割结果

图2 脑部CT图像在不同算法下的分割结果

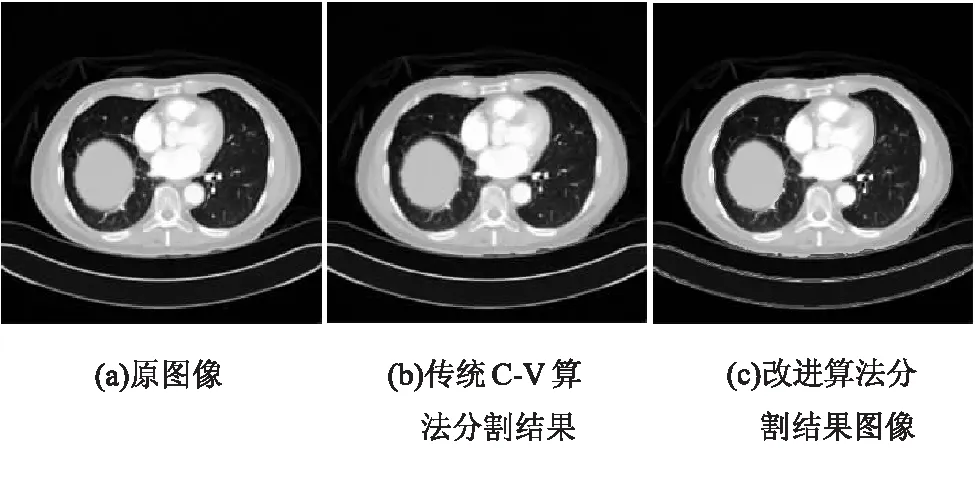
图3 肝脏CT图像在不同算法下的分割结果

从上述分割效果来看，采用改进算法相对于传统的C-V算法来讲，可以得到更明确的图像边界，包括一些细微的边界也能清晰地分割出来，达到理想的分割效果。

5 结束语

文中提出了基于Canny算子的C-V水平集模型，水平集演化曲面用Canny算子处理结果去代替，原图像先进行平滑处理，不仅分割结果更精确，而且减少了噪声对分割的干扰。实验结果表明，该方法具有普遍性，自动化程度高，不用对每一幅图像给定初始轮廓，从而提高了分割速度，拓展了使用范围。同时，分割目标可以被很好地分割出来。但由于图像种类很多，该方法对有些图像的应用效果不是很明显，日后还需完善，使算法更具普遍性。