基于概率图模型的天气预测研究
2019-07-23刘丽丹
刘丽丹
(南京航空航天大学 计算机科学与技术学院,江苏 南京 210018)
0 引 言
天气变化与人们的生活有着十分密切的关系,人们总是想方设法去预测未来的天气变化,以期能够利用有利天气,防范不利天气。传统的天气预测方法主要有天气学方法、动力学方法和统计学方法。到20世纪50年代,数值预报的出现使天气预测有了革命性的变化,是大气科学发展的一个里程碑,也是近代大气科学成为一门精细和定量化科学的标志[1],直到现在仍是天气预报的核心。但是数值模型并不能完全模拟大气运动,对于很多天气现象的发生、演变的内在机理和规律,人们尚未完全掌握,提高天气预报的准确率,仍是一个世界性难题。
目前,随着人工智能和机器学习的蓬勃发展,天气预测也迎来了新的发展机遇。一方面,机器学习方法可以用于解决数值预报分辨率低的问题,通过降尺度方法,提高预测精度。自20世纪90年代统计降尺度方法发展以来,以人工神经网络和支持向量机为代表的各种机器学习方法被应用于统计降尺度研究。1997年,Cavasos用人工神经网络降尺度预测墨西哥东北部20个站的冬季日降水[2];2006年,Tripathi等将基于支持向量机的统计降尺度模型用于研究印度月降水[3];2016年,Santri等用基于最小绝对值收缩和选择算子(Lasso[4])的分位数回归建立统计降尺度模型[5],用于预测印度尼西亚单个站点的极端降水;周璞等用自组织映射神经网络(SOM)降尺度方法对江淮流域逐日降水量进行了模拟评估[6]。这些方法都取得了较好的效果,但是,此类方法依赖原始天气模型输出产品,准确率依然受限于对天气规律的模拟程度。
另一方面,由数据驱动的机器学习方法可能帮助人们认识到更多的天气规律,它不依赖任何物理模型,能够从历史观测数据中寻找天气演变规律,进而做出预测。预测未来时间空间的气象要素值,是属于非平稳时间序列的预测问题。非平稳时间序列的预测,可以采用参数方法或非参数方法,参数方法有自回归(AR)、神经网络(NN)、支持向量回归(SVR)和隐马尔可夫模型(HMM)等,非参数方法有近邻(neighborhood)和局部拓扑(local topology)模型、非参数贝叶斯模型和函数分解等[7]。由于用于预测的自变量之间存在相关性,天气预测还要解决多重共线性的问题,适合的方法有Lasso回归、Ridge回归[8]和SVR[9]等。将这些方法用于单站天气预测,国内外研究已有很多,但关于区域多站点空间相关性的研究并不多,大气作为一个连续的系统,各站点间是有一定联系的,如果进行多站点联合预测,加入协变量相关性的考量,理论上应该能够提高预测准确率。李艳玲等用空间自回归模型预测新疆地区气温与降水量[10],对新疆地区各个测站气温和降水量之间的空间关系进行了研究,研究表明相邻地区气温和降水量的分布在空间上具有较强的相关性,但是其中的空间相关矩阵是人为设定的。在概率图模型研究领域,一些方法已经被证实可以应用于天气预测。Wytock M等给出了条件高斯图模型的一种估计方法,可以学习出随机变量间的相关关系[11],最近,Huang等提出了一种基于联合条件图套索(JCGL)的联合条件高斯图模型[12],能够学习异构协变量的条件相关性,同时预测不同地域的不同气象变量。
文中主要尝试使用易获取的国际交换站地面观测数据,应用条件高斯图模型,学习出可以从天气学角度解释的区域多站点降水量和平均气温的空间相关关系,并检验联合条件高斯图模型联合预测多站点降水量和气温在实际应用中的准确率和稳定性。
1 相关工作
概率图模型可以简洁地刻画出复杂分布的结构,具有表示、推理和学习的能力[13],现已被广泛应用于机器学习、计算机视觉、自然语言处理、语音识别、专家系统、用户推荐、社交网络挖掘、生物信息学等研究领域的最新成果中[14-15]。它以图为表示工具,最常见的是用一个节点表示一个或一组随机变量,节点之间的边表示变量间的概率相关关系,即“变量关系图”。根据边的性质不同,概率图模型可大致分为两类:一类是使用有向无环图表示变量间的依赖关系,称为有向图模型或贝叶斯网,另一类是使用无向图表示变量间的相关关系,称为无向图模型或马尔可夫网[16]。无向图中的高斯图模型,虽带有强假设,但在数学上易于处理,而且根据中心极限定理,可以较好地近似实际连续分布[17]。
1.1 高斯图模型
假设p维随机向量Y=(Y(1),Y(2),…,Y(p))服从多元正态分布N(μ,Σ),给定一个随机样本Y(1),Y(2),…,Y(n),希望估计出精度矩阵C=Σ-1,C中元素Cij=0表示Y(i)与Y(j)在给定其他所有变量的条件下相互独立,可表示为Y(i)⊥Y(j)|YSi,j。
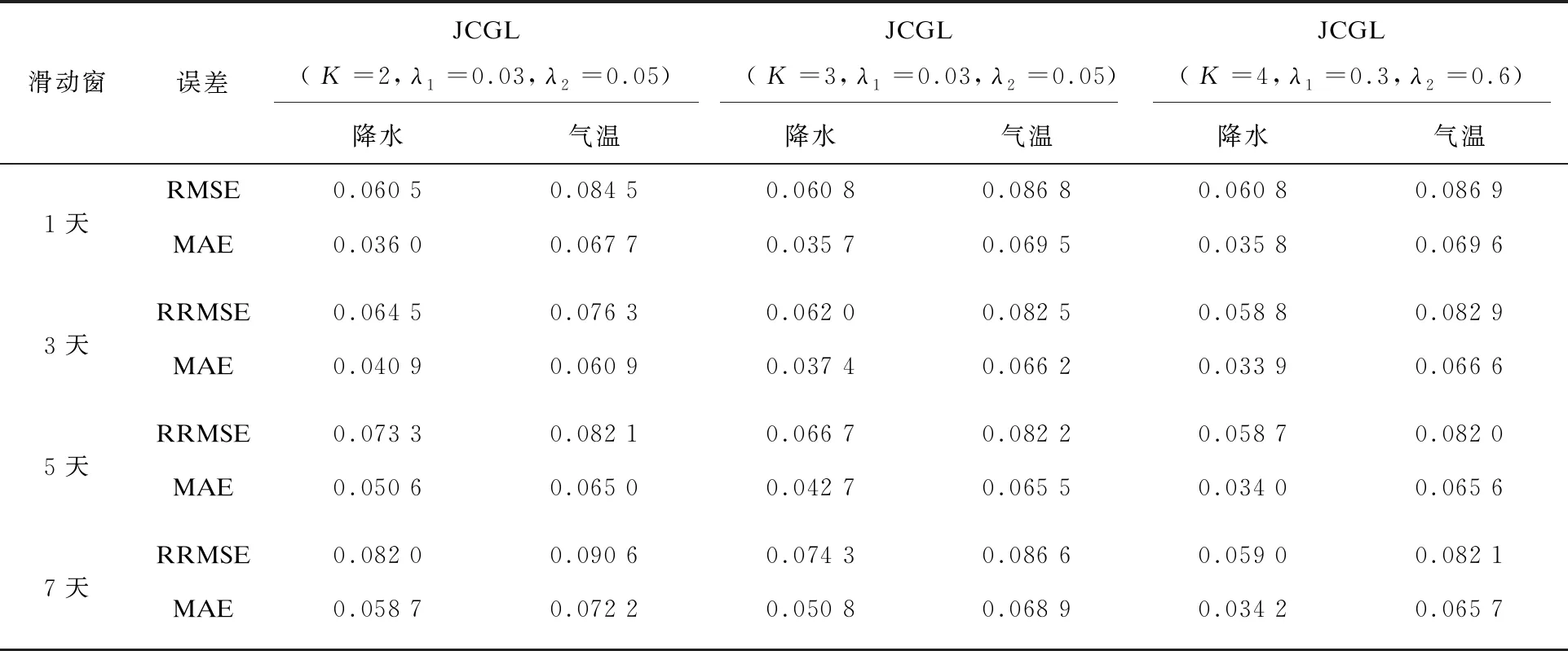
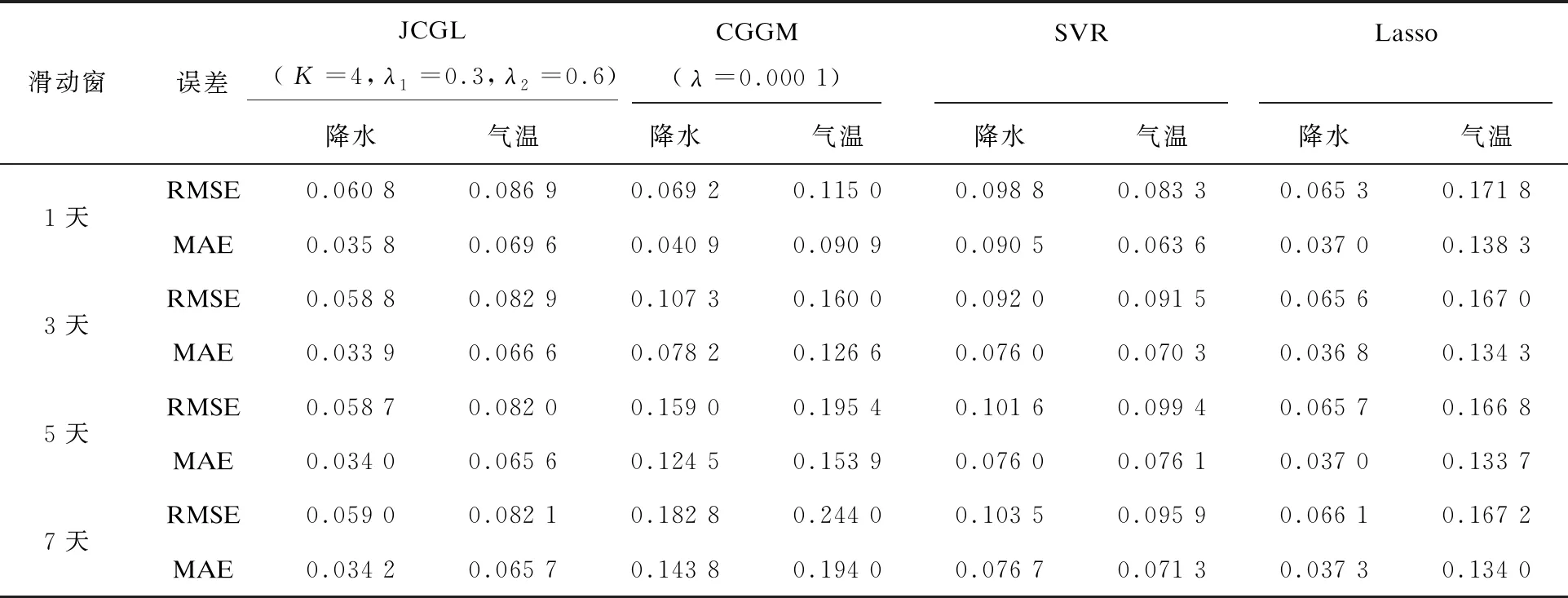
高斯图模型中,随机向量Y由图G=(V,E)表示,其中V为图的节点集,包含p个节点,E为图中节点之间的边集,E=(ei,j)1≤i 高斯图模型中的均值μ是常数,条件高斯图模型则允许均值μ随协变量x改变。Y服从条件分布: Y|x~N(Γx,Σ)(或Y|x~N(-C-1Θ-1x,C-1)) 其中,Γ∈Rp×q,Θ∈Rq×p,x=(x(1),x(2),…,x(q)),Y(i)与Y(j)条件独立则表示为Y(i)⊥Y(j)|{YSi,j,x}。这种模型不仅能模拟随机变量Y(1),Y(2),…,Y(p)之间的条件相关关系,也能模拟Y与协变量x之间的条件相关关系。此模型也可由图G=(V,E)表示。 以上两种图模型都是基于独立同分布的数据估计单个图模型,联合条件高斯图模型则可以针对异构数据进行多个图模型的联合估计,除具备条件高斯图模型的优点外,还能够刻画多个带噪声协方差的多元线性回归的联合学习。在条件高斯图模型的基础上,增加一维离散随机变量z∈N+,Y服从条件分布: Y|x~N(-Σk(Θk)Txk,Σk),k∈N+ Y(i)与Y(j)条件独立表示为Y(i)⊥Y(j)|{YSi,j,x,z=k}。此模型可由一个无向图的集合ζ={G(k)=(V,E(k)),k∈N+}表示。 输出变量Y∈Rn×p,输入变量X∈Rn×q,q=m×p,n为样本量,p为站点数,m为协变量维数,即参与预测的气象要素个数。利用条件高斯图模型,有: Y=f(X)=-C-1Θ-1X 样本对{yi,xi}i∈n的对数似然为: -log|C|+tr[SyyC+2SyxΘ+C-1ΘTSxxΘ] 应用Matt Wytock的估计方法[11],最小化负对数似然并加入1惩罚项,即: 估计出精度矩阵C,C-1即为空间相关系数矩阵。 在上述模型基础上,应用联合条件高斯图模型,联合预测K类气象要素。 为方便实现理论成果向业务应用的转化,文中应用的是1980-2011年汛期(5-9月)中国华东地区21个国际交换站的日平均气温、气压、相对湿度、风和24小时降水量等地面观测数据,来自于国家气象科学数据共享服务平台的中国地面国际交换站气候资料日值数据集(V3.0)。数据经过清理、归一化和中心化处理,以1980-2010年数据为训练集,2011年数据为测试集。 在模型预测效果评估中,采用检验回归模型较普遍的两个评价指标:均方根误差(RMSE)和绝对误差(MAE),具体表达式为: 4.2.1 空间相关性学习 用处理后的数据建立条件高斯图模型,运行1万次,取精度矩阵C的均值。如图1所示,为21个站点间的降水量相关系数可视化矩阵,显示了模型训练出的21站24小时降水量值的相关性。由于对角线上自相关性过强,为更好地展示不同站点的相关性,将对角线值改为0,方便对比。 由图1可见,对角线附近的地理位置靠近的站点呈正相关,距离越远相关性越小,不同气候区的站点会有明显的负相关。例如:上海、杭州与定海(舟山)地理位置较近,处于长江口到杭州湾一带,明显正相关;福建中西部三个站福州、南平和永安也明显正相关;南京则与江淮流域的几个站点蚌埠、合肥、霍山、东台正相关;定海与徐州明显负相关,前者滨东海,处杭州湾,后者处淮河以北,为苏鲁皖交界,相同的降水过程却很少能同时影响此两处;安庆与永安也明显负相关,安庆(N30°37′,E116°58′)处长江下游,永安(N25°58′,E117°21′)则位于武夷山以南,两地经度相近,南北相差500公里左右,也很少会受相同降水过程影响,相反,夏季当永安处于副热带高压控制时,为晴好天气,安庆则会处于副热带高压的边缘多雨带,而当有台风影响永安造成降水时,安庆通常会处于台风北侧高压控制,没有降水。 图2为21站平均气温的相关系数可视化矩阵,同样将对角线的自相关系数设置为0。可见华东地区夏季各站平均气温均呈正相关,且距离越近相关系数越大,相关系数最大的是南京与东台、景德镇与南昌、景德镇与衢州,由国家气候中心提供的2018年6月平均气温距平图(图3)可见,南京与东台气温变化同步,景德镇、南昌和衢州气温变化也同步,具体原因尚有待分析。 图2 华东地区21个站平均气温相关系数 图3 平均气温距平图 4.2.2 地面气象要素预测 在使用联合条件高斯图模型预测的实验中,不同的滑动窗口大小和预测类数会导致不同的预测误差,以预测未来24小时降水量和平均气温的误差做参考,结果如表1所示。预测类数K≤3时,滑动窗口越大,预测误差越大,而K越大,降水量预测误差越小,平均气温预测误差越大;当K=4、滑动窗口为5天时,降水量预测误差最小;K=2、滑动窗口为3天时,平均气温预测误差最小,当K>4时,误差与K=4无明显变化。说明在输入变量维数不变的情况下,并不是输出类数越多,预测效果越好,也不是滑动窗口越大,预测效果越好,在具体应用中,要充分考虑输出变量间的结构关系,通过对比,找到最合适的参数。 表1 联合条件高斯图模型不同参数预测效果对比 分别建立SVR回归模型、Lasso回归模型、条件高斯图模型和联合条件高斯图模型,对21个站点进行降水量和气温预测实验,每个模型重复实验100次,取RMSE和MAE的均值进行比较,结果如表2所示。可以看出,联合条件高斯图模型好于条件高斯图模型,也好于SVR和Lasso。 表2 不同模型降水与气温预测性能对比 概率图模型在天气预测上的应用价值已被证实,文中验证了两种概率图模型在天气预测实际工作中的应用可行性,通过采用从业者可以实时获取的国际交换站地面观测数据,实现了应用条件高斯图模型学习各观测站点间气象要素的条件相关性,并给出了天气学解释和验证;应用联合条件高斯图模型,解决了多站点未来24小时降水量和平均气温的联合预测问题。实验结果表明,条件高斯图模型能够刻画出响应变量之间的条件相关性,在天气预测上可以给出合理解释;联合条件高斯图模型不仅能够实现多任务输出,由于考虑了气象要素间的相关性,预测能力较条件高斯图模型有所提升,且优于SVR和Lasso回归。1.2 条件高斯图模型
1.3 联合条件高斯图模型
2 空间相关关系学习模型


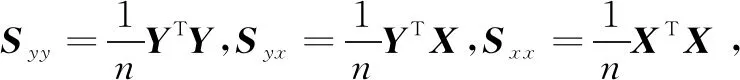
3 多要素联合预测模型

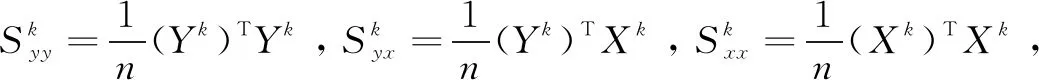
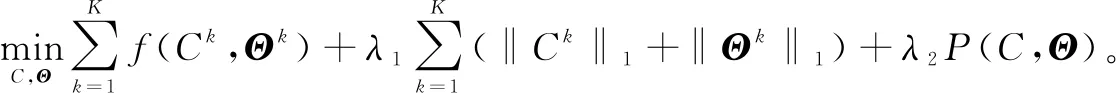
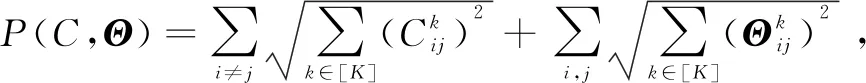
4 实验与结果分析
4.1 实验数据与评估标准
4.2 实验结果


5 结束语
