多尺度多类中性模糊聚类图像分割算法

2019-07-23温金玉宣士斌黄亚武肖石林

计算机技术与发展 2019年7期

温金玉，宣士斌，黄亚武，肖石林

(广西民族大学信息科学与工程学院，广西南宁 530006)

1 概述

随着计算机技术的日渐成长，图像分割技术逐渐受到海内外研究者的高度重视[1]，分割算法也如雨后春笋般涌现，如基于特殊性能区域识别分割[2]、基于不规则组织与规则组织的方法[3]、基于数据融合方法[4]、基于混合方法[5]，还有基于模糊理论的分割方法。文献[6]先通过像素之间的灰度与间隔来说明像素之间的相似度，轮回地迭代出图像的超像素，继而选取每一个超像素的小波能量特质，并利用模糊C对提取到的特征进行聚类。该方法分割精确度高，能有效抑制孤立点影响，但是当噪声复杂的情况下，抗噪能力较差，时间复杂度也高。文献[7]操纵像素的空间范畴信息映射出的二维直方图作为FCM的聚类样本，以减缓样本空间的维度，有效解决了传统聚类算法速度慢的问题，分割结果也有效，但是抗噪性能有限。文献[8-9]是基于超像素的图像分类，能灵活地减少噪声与独处点的影响，也能够一定程度地提升处理的性能，但是该算法比较耗时，计算复杂度高。Gong Maoguo等[10]提出改进的基于局部信息的FCM，联合局部空间与灰度信息来产生新的局部范畴的模糊因子，该模糊因子不含任何参数。该算法在迭代过程中利用了原始图像，防止预操作可能会致使细微部分的失真。然而，因为其架构的部分空间的限制，致使分类过程中产生部分细节的失真。Pinti Antonio等[11]提出将动态窗口与图像中空间数据挖掘算法进行融合，采用FCM的标准目标函数，并用n维特征阵描述图像中的每个像素。

该方法在真实图像上取得了满意的效果，但未能对背景、皮质骨、可延展的颚骨、脂肪肉、肌肉及大腿等核磁共振成像进行有效分类。Zhao Zaixin等[12]联合了图像块和部分空间信息，并增加一权值函数表示，通过结合加权的高斯欧氏距离提出了领域的FCM加权算法，能有效地保留图像有组织的信息，对无噪图像或含噪强度较低的图像能获得相比大的分类精度，然而当增大噪声强度后，分割精度不高。并且，分割过程当中对图像的中间像素考虑不足，便于形成边沿恍惚。Siu Kai Choy等[13]提出基于模糊模型的聚类算法，该算法将器量广义几率分布之间空间差距的Kullback Leibler间隔引入到模糊聚类的目的函数中，获得一种模糊广义高斯密度分割。算法的优点是对初始参数不敏感，并有效地分割不同的纹理图像，具有较好的分割效果，但抗噪性弱。

目前，也有许多基于最大后验概率的图像处理方法，例如Jian等[14]提出了一种改进的基于ICA统计估计的SAR图像去噪方法。但是这些方法必须假定先验概率分布，然而，真正的分布是很难符合所有的SAR图像遵循相同的分布。Mohamad M等[15]提出结合融合方法进行分割，该交融过程首先依赖于小波变换技术，运用技术在不同的参数下运行好几次。交融的图像与小波技术联合，增进了分割的准确性。然而，较佳的成效得要先探寻到较优的融合方式，验证过程的期间复杂度相对冗长。

最近很多的研究者对模糊的聚类方法进行了研究，新的分类方式如中性均值聚类(neutrosophic c-means clustering，NCM)[16]，可以将数据集进行有效分类，并获得了较精确的分割。但是，该方法在定义模糊类的聚类中心时使用的是最大与次大的隶属度的平均值，这样未充分考虑每个样本点对于每一类的隶属情况，不能自适应。

近来，文献[17]提出了一种新的分割方法，结合中性均值聚类和不确定性滤波(neutrosophic c-means clustering and indeterminacy filtering，IFNCM)。IFNCM是在NCM的前后加了一个不确定性滤波器。根据中性图像中的不确定性值来定义一个新的滤波器，即不确定性滤波器。对于不确定性子集域创建不确定性高斯滤波器，在某种程度上可以降低噪声，但是由于不确定性子集本身的不确定性和模糊度使得参数的选择不可能完全正确。

针对上述文献存在的问题，文中利用确定性子集的数据分布来确定模糊类子集的聚类中心。同时引进自适应的权重因子，依据确定性、模糊类和噪声类的样本数目占有的比例定义每次迭代过程中的权重系数，以提高分割精确度和收敛速度。对图像的预处理，引入了小波去噪，采用阈值去噪的方法分别处理小波分解的高低频系数，在去噪的同时能有效克服一般平滑去噪会去除一些边缘信息的问题，此阈值的获取用最大熵原理。

与已有的聚类分割方法相比较，该方法分割精确度高，不仅有良好的分割效果，而且也大大提高了收敛速度。

2 相关理论

小波分析具备多分辨率分析的特点，其特征是一种建立在函数的空间概念上的理论。小波在时域与频域都有表征信号部分信息的能力，在信号平稳时能用较低的时间分辨率来提升频率的分辨率。在频率转变不大时能够用较低的分辨率来获取到精准的时分位置。

去噪方式包括平滑去噪和小波去噪，也有多方法融合去噪，如文献[18]先采用中值滤波方式对图像去噪，其中权值是自适应的。然后对已去噪图像实行小波分解，分解后将差异子带采用异同的滤波方式进行滤波，其中低频部分采用低通滤波器滤波，高频分量用中值滤波，最后进行小波重构。这样从理论上也可以认为是有一定去噪效果的，但从实际对含噪图像去噪处理的实验结果可以发现，该方法在去噪的同时也忽略了一些细节部分，特别是边缘的细节信息在平滑过程中也被平滑了，如图1的左图所示。

图1 文献[18]与文中去噪方法的比较

整体看很模糊，具体看人的鼻子、嘴巴都没有准确定位，相机的摄像头部分也都被模糊化了，不能看清边缘的细节。文中采用的去噪方法充分地考虑了高低频分量的特性，对高频采用阈值法去噪，将低频进行阈值分割，实验结果较为明显，特别的摄像头的齿轮都可以清晰显示，还有人的轮廓信息都比较清楚，保留了更多的细节部分，整体效果没有被虚化。这也是文中方法的一个优势。

3 多尺度多类中性模糊聚类的图像分割

中性模糊聚类(neutrosophic fuzzy clustering，NFC)是在中性均值聚类[16]基础上的改进。文中算法的目标函数同参考文献[16-17]，如下：

(1)

从式1可以发现前面两项均是传统聚类的拓展，表示确定性聚类与边缘区域的类别，但第三项跟聚类原型无关，可见这部分将作为噪声数据集合。N为样本数目，C为类别数，m为模糊因子，w1、w2、w3分别为三个权重因子，δ为异常值的数量，Cp为新定义的模糊项聚类中心。

在基于模糊聚类的图像分割中，最容易产生错分的是位于不同类相连接区域的像素点。事实上，NCM就是为解决此类问题而提出的，但其用于控制边缘区域的第二项中的中心点Cimax总是由样本点xi的隶属度最大的两个类确定，未充分考虑到每个样本点对于每一类的隶属情况。

3.1 基于中性均值聚类的模糊重定向

对于模糊类的聚类原型，用Cp表示：

(2)

(3)

(4)

其中，pi和qi分别为T的最大与次大值。文献[16]是根据确定性隶属度T的最大和次大数所属的类别数的平均值来决定模糊集的中心，这种定义不能充分考虑到每个样本点隶属每个类的情况，不能自适应。

文中用Cp表示模糊子集的聚类中心，这个中心根据隶属度的数据分布可以分为两种情况，除了最大的隶属度外其他均小于阈值的时候，Cp等于最大隶属的那类中心；另一方面是只有当两个以上隶属度超过阈值，那么Cp就等于最大和次大隶属度所属类中心的平均值，它的值是由每个数据点i的常数数目计算的，当然该阈值为每个点隶属于每个类的最适阈值，用tt表示。可以确定的是，当几个数据属于某一类的可能性最大时，加上比其他的隶属度大很多的情况下，次大的隶属度已经没有多大的意义，所以说Cimax的值并不能减轻不确定程度，反而加大了模糊程度。

接下来是最优化目标函数，通常使用拉格朗日方法最小化算式1，构造拉格朗日目标函数：

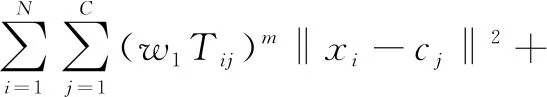
Ii+Fi-1)

(5)

最小化拉格朗日方程使用的操作是计算每个未知元素的偏导数，例如Tij，Ii，Fi和cj,使用指定的欧氏范数，让各阶导数等于0，得到如下公式：

(6)

(7)

(8)

(9)

(10)

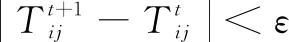
3.2 基于最大熵的小波去噪预处理

二维小波分解可以在水平与垂直方向分别处理，一幅图可以在每个尺度上被分解为四个通道，每个通道上的小波系数能量都代表着图像空间和频率的主要信息，可以作为图像纹理分析的特征[19]。运用小波阈值去噪方法，根据最大熵定理求阈值的具体过程如下:

(1)小波分解成三层，提取到各层分化的低频与高频部分。对各层三个高频分量采用最大熵的原理得到自适应的阈值，分别对高频系数分量进行阈值化去噪处理。

(a)根据图像的直方图信息求出所有的可能灰度，计算图像的大小，并求出各灰度点出现的概率hi，及横纵方向的概率之和并记为P1、P2；

过度的流失会给酒店带来顾客忠诚度降低、经营成本提高等后果。近几年来我国酒店员工流失率不断升高甚至已远远超过酒店行业员工流失的基本标准15%。酒店员工流失大多数为基层员工，而正是这些基层的一线员工才反映了一个酒店的服务质量，由此可见，酒店员工流失率对酒店的服务质量和发展有着极为重要的影响。

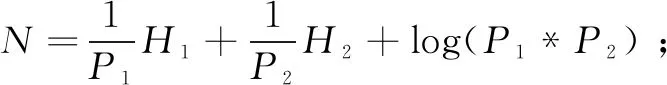
(d)根据高概率的事物总更容易出现的情况来选择N中最大的概率，并相应的找到其所对应的点，即为要求的阈值分割点。

(2)在逐层重构前先对低一层的低频分量进行阈值分割，比阈值大的保留，否则置为零。

最后，文中方法具体步骤如下：

Step1：预处理阶段。

(a)利用维纳滤波对图像进行初步去噪；

(b)用小波阈值去噪进行深度去噪。

Step2：用NFC方法将预处理过的图像进行分割。

(a)通过传统的模糊分类算法将图像分为三个子集，即初始化T，I与F，并计算出初始的权重因子w1，w2，w3。设置调节参数(C、m、δ、ε)，ε是迭代终止参数；

(b)利用式9计算各类别聚类中心，同时通过式2根据T的值来计算模糊聚类中心Cp；

(c)用式6～8分别更新三个子集T',I'与F'；

(d)判断终止条件，若|T'-T|<ε则结束迭代，否则跳到步骤b循环继续；

(e)根据确定性子集T得到聚类结果。

4 实验

根据上文所述，在中性模糊聚类分割的过程中结合小波变换，使得文中方法在分割的实现上，完美地控制了噪声的干扰，也避免了图像边缘的失真现象，使得分割速度快，分割效果更佳。在小波去噪中设置尺度向量为[2 2 3]能得到更好的效果，分别设置调节参数m为2，δ为50，ε为0.000 1，权重因子分别设置为w1=0.7，w2=0.15，w3=0.15。接下来证明其有效性，具体情况如图2所示。

图2中(a1)为传统的模糊均值聚类方法，可以看出分割效果一般，左裤腿上有被分段的情况，可能是由于噪声的影响，使得湖面与人的左腿裤脚地方也有了错乱的聚类现象，导致分割的结果不怎么完好。(a2)为文献[10]的方法，不给模糊因子任何参数，也就是让其自适应，这样可以提高收敛速度，但是会导致一些细节部分丢失，使得分割精确度不高，与(a1)相比分割效果更佳，如右下角孤立点更少。文献[13]是基于广义高斯分布的模糊聚类，在求高斯密度的时候要用到估计的方法，该方法自带随机性比较高，所以也会更大尺度地影响着分割结果。如(a3)所示，人的上衣及裤腿的分类情况比其他方法有很大的差别，一些细节部分信息也容易丢失，如支架的中间部分与末端。文献[16]是基于中性集的思想的模糊聚类，可以获得较精确的分割，如(a4)所示，摄像师的头部纹理特征及摄像头的轮廓都可以较清晰地显现，但摄像师右裤脚及水面还是有一些孤立点，可能是噪声引起的。图(a5)是文献[17]的算法实现，该算法也是对传统的模糊聚类进行的改进，可以看出其效果较前几种更佳，但也有一些缺陷，如摄影师的鼻子与下巴几乎是被分错类了，还有右腿裤脚部分，细心看就可以看到有两个白点，这也是误分的结果。(a6)是文中方法，与其他方法相比分割效果较好，对细节的信息有较好地保留。

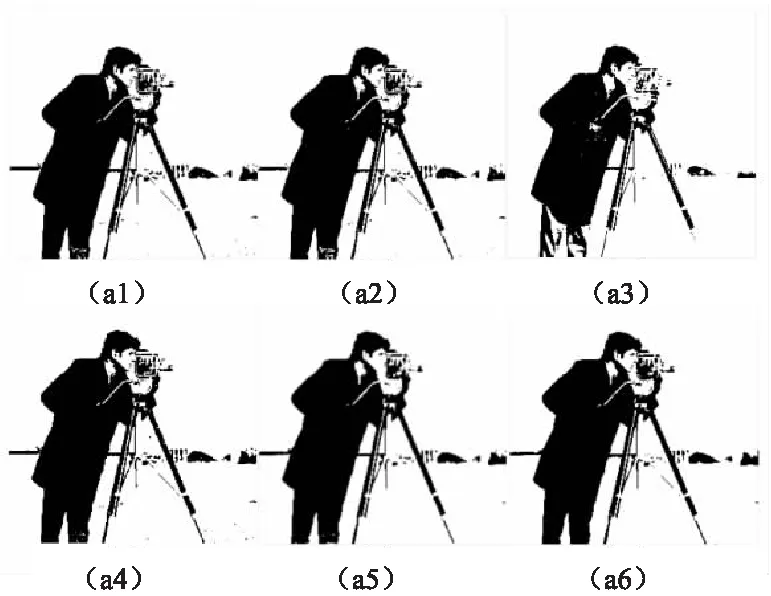
图2 多种算法对摄像师图像的实验比较

精确度优劣的问题，因单从视觉上比较难分辨高低，文中从计算像素聚集数量的区间比例进行客观的评价。根据直方图来划分区间，对使用不同的方法分别取对应区间的像素点数，计算处理后该区间的数量与原图差异的大小也可以用来说明正确率的高低，即精确度也成正比，表1为对其中的三个区间(0-130，130-200，200-256)的取样情况，通过与原始图像该区间数量之差所占比例判断精确度。

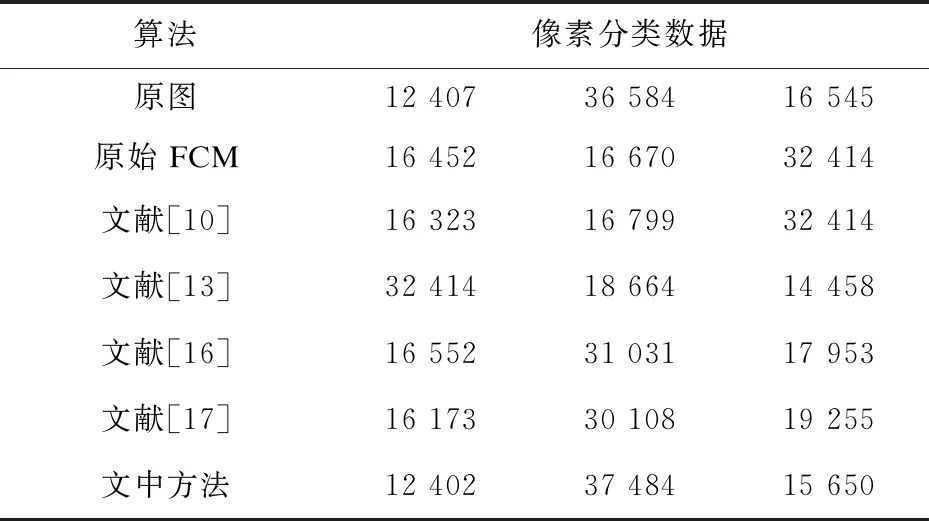
表1 多种算法对摄像师图像的数据分析

表1列出了各种方法在每个区间的数量显示和原图的数量大小比较，可以发现文中方法与原图的差异最小。该图是以不同像素区间的数据显示，原图在0-130区间的样本点共有12 407个，在130-200区间所占比例最大，达到了36 584个，剩下的也有16 545。这说明只要图像处理后的数据分布能与原图保持一致或是相差不大的情况下精确度高，分割效果更好。此外，原始聚类、文献[10]与文献[13]的数据分布是一头大，剩余的较平均小。而文献[16]和文献[17]及文中方法同原始数据一样，是中间大，两头小。但再细心地看，文中方法显示的两头数据同真实数据更加接近。所以可以证明文中方法分割的精确度相对较高。接下来通过实验再来测试各方法对噪声的鲁棒性。

在图1中加入高斯噪声(方差为0.01)，分析它们的平均绝对误差与信噪比数据，如表2所示。

表2 平均绝对误差的数据分析

表2是针对摄像师含噪情况下的各种方法处理后的平均绝对误差(MAE)数据显示，该值越小代表效果越好。从MAE的5个值可以看出，进行了5次试验比较分析，MAE1到MAE5添加的噪声都是高斯白噪声，但是方差略有千秋，分别是0.01、0.02、0.05和0.1。可以看出，文献[13]与文献[16]对噪声更敏感，特别是文献[16]，随着方差的增加其MAE值也在不断上升。文中方法对函数图像处理效果较好，不管方差是否变化MAE值均小于其他方法，且MAE值跨度不大。

表3 信噪比的数据分析

表3是在含噪情况下各个方法处理后的信噪比(SNR)数据显示，该值越大代表效果越好。原始的模糊聚类与文献[10]的SNR差不多，文献[13]与文献[16]会相对小一些，文献[17]的SNR变化跟不同的方差没有关系，总体比文献[13]与[16]好些，但劣于文中方法。不管是添加哪个方差的噪声，文中方法的SNR都比其他方法大，而且值都在8～12直接上下波动。从以上两个数据统计数据可以证明文中方法的抗噪能力较强。