三支概念分析研究现状与展望

魏 玲，高 乐，祁建军

(1.西北大学 数学学院,陕西 西安 710127；2.西安电子科技大学 计算机科学与技术学院,陕西 西安 710071；3.西北大学 概念认知与智能研究中心，陕西 西安 710127)

三支概念分析理论(Three-way concept analysis,3WCA)是将三支决策理论(Three-way decision,3WD)应用于形式概念分析(Formal concept analysis,FCA)产生的一种进行知识发现的理论。它既体现三支决策理论“三分而治”的思想,也具有形式概念分析理论的基本表现形式和具体的研究内容。自2014年提出以来,其思想逐渐为知识发现研究领域的研究人员接受,研究主题与理论成果也越来越多。

本文对有关三支概念分析的文献进行梳理,并对其今后的研究方向进行了探讨。

1 形式概念分析理论

本节主要从FCA理论的发展过程、研究内容及研究现状等角度介绍FCA理论。

1.1 FCA理论的产生

20世纪70年代时期,格论已经发展相当完善。德国数学家Wille曾指出[1],格论“在理论概念、结论和发展等方面有丰富的成果,其中有一些甚至是精致的头脑体操”。但是,他同时也指出,“该理论与周围事物的联系越来越弱,可能会导致该理论或其中一部分变得越来越孤立。”

为解决格论数学味太浓、过于抽象、难以应用的问题,并推动格论研究者与应用者之间的联系,Wille提出了重建格论的想法,给出了一个可理解的格的实际例子:哲学中“概念”的形式化描述以及所形成的格结构。他将其命名为“形式概念”与“概念格”,后逐步发展成为形式概念分析理论。

形式概念分析理论以对象集与属性集以及二者之间二元关系形成的“形式背景”为基础,借助对象子集与属性子集之间的对偶算子,形成内涵与外延,使得哲学中的“概念”可以用数学的形式来刻画;进而形成能够可视化表达的概念格,在背景和概念层次分析的框架下,研究格的结构与表示理论。

1.2 FCA基本理论

FCA的数据基础是一个形式背景(G,M,I),其中,G是对象集,M是属性集,I是G与M之间的二元关系。若对象g∈G具有属性m∈M,则记为gIm。

在对象子集X⊆G和属性子集B⊆M上可以定义一对对偶算子:

X*={a|a∈M,∀x∈X,xIa}

B*={x|x∈G,∀a∈B,xIa}

X*表示X中所有对象共同具有的属性集合,B*表示共同具有B中所有属性的对象集合。

如果一个二元对(X,B)满足X*=B,且B*=X,则称(X,B)是一个形式概念,简称概念。其中,X称为概念的外延,B称为概念的内涵。其语义与哲学中“概念”这一名词所含的两部分:外延与内涵一致,是哲学中“概念”的形式化描述,故称其为“形式概念”。

用L(G,M,I)表示形式背景(G,M,I)的全体概念,记

(X1,B1)≤(X2,B2)⟺X1⊆X2(⟺B1⊇B2)

则“≤”是L(G,M,I)上的偏序关系。若(X1,B1)和(X2,B2)是概念,则

(X1,B1)∧(X2,B2)=(X1∩X2,(B1∪B2)**)

(X1,B1)∨(X2,B2)=((X1∪X2)**,B1∩B2)

也是概念,从而L(G,M,I)是格,并且是完备格,可以用Hasse图直观刻画。

例1表1是一个形式背景(G,M,I),其中,对象集G={1,2,3,4},属性集M={a,b,c,d,e}。如果对象与属性有关,就在对象行与属性列的交叉处用1标记,否则,用0标记。其概念格如图1所示。注:按照FCA理论的习惯,本文所有例子中,除全集G与M外,一律用集合中的元素序列来表示一个集合。以形式概念(24,abc)为例,{2,4}是外延,{a，b，c}是内涵,表示对象2与4共同具有的属性是a,b和c,而共同具有这3个属性的对象也恰为2和4。

表1 形式背景(G,M,I)Tab.1 A formal context (G, M, I)

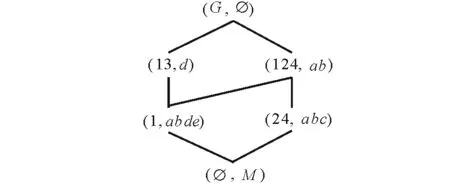
图1 例1的概念格Fig.1 Concept lattice of Example 1

1.3 FCA研究热点

形式概念分析理论最根本的贡献和核心是对概念的数学化和形式化的描述,以及以此为基础形成的概念格结构。由于形式概念有很好的语义,这使得形式概念分析演变为相对独立的研究分支,在概念格的建造、简化、属性约简、规则提取等方面已有很丰富的成果,成为了一个新的有影响力的研究方向。

近年来,结合信息时代、多学科多理论交叉融合的特点,形式概念分析与其他相关理论的支撑和互补使其进一步蓬勃发展,特别是与粗糙集、粒计算、模糊集、三支决策理论等的结合,涌现出一大批成果[2-8],并应用到诸如信息检索、语义web、知识工程、管理科学等很多领域。

李金海、吴伟志[9]从Galois连接的粒计算模型、对象粒化、属性粒化、关系粒化、关系诱导的概念粒化、粒规则、粒约简、粒概念、粒概念学习、概念粒计算系统等角度展示形式概念分析的粒计算方法的主要研究内容,并针对大数据与认知学习提出若干挑战性问题。有关讨论结果将为形式概念分析的粒计算方法的研究与发展提供借鉴。

1.4 FCA优劣势分析

FCA的优势与劣势是共存的,每一个优势的背后都有潜在的劣势,就好像一把双刃剑。比如,形式概念是哲学名词“概念”的形式化,可以表达内涵与外延之间的一种平衡美,语义严谨,但同时这也是对对象子集与属性子集之间关系的一种要求苛刻的刻画;格结构具有层次性、可视化的优点,能直观体现类的泛化与例化,但是却比等价类复杂,且建格是NP难问题,所以使用FCA时是否有必要每次都要先建格,即可视化是否总是必要的?而这也成为FCA理论的应用受局限的最重要的原因。

2 三支概念分析理论的基本思想

3WCA是将3WD的思想应用到FCA理论中,扩展形式概念的语义和形式得到的。

3WD的主要思想是三分而治,是基于“三”的思维方式、问题求解方法和信息处理模式,是三元论和三分法。其目标是将一个论域分为两两互不相交的3个部分,而这3个区域在一个具体的决策问题中可以分别被看作是接受域、拒绝域和不承诺域。相应于这3个区域,可以建立三支决策规则[10-16]。

2.1 3WCA的产生

Wille在形式背景基础上给出的形式概念我们可以称之为经典概念,因为这种概念最早、也最为纯粹的用形式化的方式反映出“概念是内涵与外延的统一”,完美的以数学的形式表现出了哲学当中的概念。

但是,尽管形式概念反映了内涵与外延之间的统一、彼此拥有的共存特点,然而直观上还有一种信息没有反映出来,即作为外延的对象子集所共同不具有的属性和共同不具有作为内涵的属性子集的对象。而这也是一种“共性”,而且,在仅考虑“共同具有”的特点时,对于属性集或者对象集仅仅做到了二分。

从三支决策的角度看,3WCA是一个具体模型;从形式概念分析的角度看,它是对FCA的推广;从粒计算的角度看,它又是对知识粒(概念)更精细和完整的描述。

2.2 3WCA基本概念

3WCA的基本概念是三支概念以及三支概念格。按照从对象出发,将属性集三分的理念,可定义对象导出三支概念和对象导出三支概念格;对偶地,按照从属性出发,将对象集三分的角度,又可定义属性导出三支概念和属性导出三支概念格。

为了定义“共同不具有”这个意义,Qi等给出了负算子的概念,而将Wille提出的经典算子相应的称为正算子。

就金融的功能而言，商业银行向各大产业客户提供间接融资并生成基础资产，其他非银行金融机构向社会公众提供各类投资品及保障品并生成特定资产，还有的金融机构把这类资产及由此衍生的收益或风险证券化，为社会提供更高层次的投资产品及风险规避产品，如ABS、CDS等，并配套形成规则清晰的获取风险收益及转移风险的资产衍生化机制和市场。对存有另类不确定性风险的技术研发融资，则要靠专门的风险投资(VC)去评估并解决。

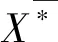
结合正、负两种算子,即可同时反映两种共性,于是得到对象导出三支算子(OE算子)与属性导出三支算子(AE算子)[17,21]。

定义1设(G,M,I)是一个形式背景。对于任意的对象子集X⊆G和属性子集A,B⊆M,一对OE算子

(OE1)<·:P(G)→DP(M)

(OE2)·>:DP(M)→P(G)

定义如下:

(X, (A,B))称为(G,M,I)的一个对象导出三支概念,简称OE概念,当且仅当,X<·=(A,B)与(A,B)·>=X同时成立。X称为OE概念(X, (A,B))的外延,(A,B)称为内涵。

从OE概念出发,我们可使所有OE概念组成的集合OEL(G,M,I)形成一个格,称之为对象导出三支概念格(简称OE概念格),其中的偏序关系为:

(X,(A,B))≤(Y,(C,D))

⟺X⊆Y⟺(C,D)⊆(A,B),

上、下确界为:对于任意的(X, (A,B)),(Y, (C,D)) ∈OEL(G,M,I),

(X,(A,B))∨(Y,(C,D))=

((X∪Y)<··>,(A,B)∩(C,D)),

(X,(A,B))∧(Y,(C,D))=

(X∩Y,((A,B)∪(C,D))·><·)。

对偶的,我们也定义了一对AE算子,并形成AE概念以及AE概念格。

图2 例1的对象导出三支概念格Fig.2 OE lattice of Example 1

图2是例1的对象导出三支概念格,我们以对象导出三支概念(13,(d,c))为例解释其语义。从3WD角度:从对象子集{1,3}出发,可以将属性全集三分为{c},{d}与{a,b,e};从FCA角度:对象1与3共同具有的属性是d,共同不具有的属性是c;共同具有d、同时共同不具有c的对象也恰为1与3;而{c}∪{d} 的补集中的属性则是对象1与3具有差异的属性。所以,该三支概念清晰、完整、准确的反映了一个对象子集的共性(包括正面的和负面的两种共性)与差异性,以及对于属性集的三分。

图3是例1的属性导出三支概念格,其中概念的解释与对象导出三支概念类似,只不过是从属性角度出发,考虑一个属性子集被对象集共同具有以及共同不具有的情况。

图3 例1的属性导出三支概念格Fig.3 AE lattice of Example 1

从图2与3可以看出,这两个三支概念格明显比图1的经典概念格复杂,这是信息反映更为精细所付出的代价,自然也直接导致3WCA应用受限。

3 三支概念分析研究现状

由于3WCA是FCA与3WD结合的结果,形式概念分析的优劣势等问题以及研究热点也被带入到3WCA中。因此,3WCA的研究内容主要包括:与FCA的关系,以及FCA中相关研究的平行研究,比如三支概念格的建格算法、属性约简、规则提取等;与三支概念格自身特点相关的研究内容包括:不完备背景上的知识获取、冲突分析问题的解决方法、对边界域中的对象(属性)的深入研究、序贯三支概念格等。

3.1 3WCA研究成果

由于3WCA是对FCA的扩展,因此,很多FCA中的研究内容可平移到3WCA中,而目前的研究也多属于这个范围。

3.1.1 3WCA基础理论研究 Qi等提出三支概念分析后,从元素、集合和序的角度分别分析了对象/属性导出三支概念格与经典概念格之间的关系,并给出了在经典概念基础上构造三支概念的充要条件以及相应算法[17-18]。

Ren等[22]研究了对象/属性导出三支概念格的4种属性约简问题及计算方法,并讨论了其间的关系。

陈雪等[23]针对两种三支概念格,在AE(OE)协调的决策形式背景下,研究了保持AE(OE)非冗余规则信息不丢失的属性约简理论,并给出了计算方法。

林洪等[24]提出了三支粒协调决策形式背景以及三支粒协调集的概念,结合区分矩阵和区分函数给出了三支粒约简方法,并讨论了决策形式背景下三支粒约简、粒约简、分类约简之间的关系。

Yu等[25]主要对可以用三支概念格表示的完备格的特征进行了研究,包括原子和不可约元等特殊元素的性质,完备格可被表示为三支概念格的条件等,并对三支粗糙概念格进行了类似的讨论。

3.1.2 三支概念格构建 祁建军等[26-27]针对三支概念分析理论中三支概念数量庞大、构建耗时的问题,提出了一种三支概念的并行构建算法PCbO3C。其以提高三支概念的构建效率为目标,在三支概念串行构建算法CbO3C的基础上进行并行化改进,利用多线程技术并行计算给定形式背景的所有核心三支概念。

Qian等[28-29]先将形式背景进行同构转化,进而利用并置或叠置方式构造三支概念格,并对经典概念格、三支概念格,以及三支面向对象(属性)概念格的构造进行了研究,探讨了它们之间的关系。

王明等[30]利用 K-Modes 聚类方法对OE-概念进行聚类,通过类中心获得子背景,进而通过定义K-删除变换研究原背景OE-概念格与子背景OE-概念格之间的关系,实现OE-概念格的压缩。

3.1.3 针对决策形式背景进行规则提取 刘琳等[31-33]给出了决策形式背景在属性导出三支概念格下的规则提取方法,首次提出了负规则。并研究了如何利用置信度从背景提取非冗余对象导出三支规则以及如何利用概率分布解决一些实际问题。

3.1.4 概念学习 Li等[34-36]从认知的角度提出了一种利用多粒度描述三支概念的公理化方法,并设计了一个三支认知计算系统寻找三支认知概念,同时利用集合近似的概念模拟从给定线索学习三支认知概念的认知过程;从信息融合的角度,针对海量数据和多源数据研究了学习三支概念的并行计算技术。

3.1.5 模糊三支概念分析 He等[37]将模糊逻辑的基本思想引入到三支概念分析的研究中,定义了L-模糊三支算子及其逆算子,给出了L-模糊三支概念,构造了相应的概念格。

Singh[38]则是从中智集的角度研究了三支模糊概念格的描述问题,探讨了其诸多性质。

3.1.6 不完备背景的三支概念获取问题 形式概念与三支概念都是在完备形式背景的基础上获取的,但我们更多面对的是信息不完整或者不明确的不完备形式背景。

Burmeister 和Holzer将不完备形式背景定义为一个四元组K=(G,M,{+,?,-},J),其中J是一个三元关系J⊆G×M×{+,?,-},具体解释如下[38]:

(g,m,+)∈J:已知对象g具有属性m,

(g,m,-)∈J:已知对象g不具有属性m,

(g,m,?)∈J:对象g是否具有属性m未知。

表2是一个不完备背景的例子。

表2 不完备背景(G,M,{+,?,-},J)

在不完备背景中,无法用形式概念分析中的常规导出算子获得一个对象集共有的属性或者共有某些属性的对象集。根据三元关系的解释,Burmeister与Holzer将形式概念分析中常规的导出算子扩展为模态形式的导出算子[39],Yao在此基础上,引入不完备背景的完备化思想,利用区间集理论,给出了部分已知概念的外延和内涵的区间-集合表示[40-41]。

假设概念的形式依然是二元对(外延,内涵),那么根据外延与内涵分别为经典集或者区间集可以得到4种不同的概念,其关系如图4所示。

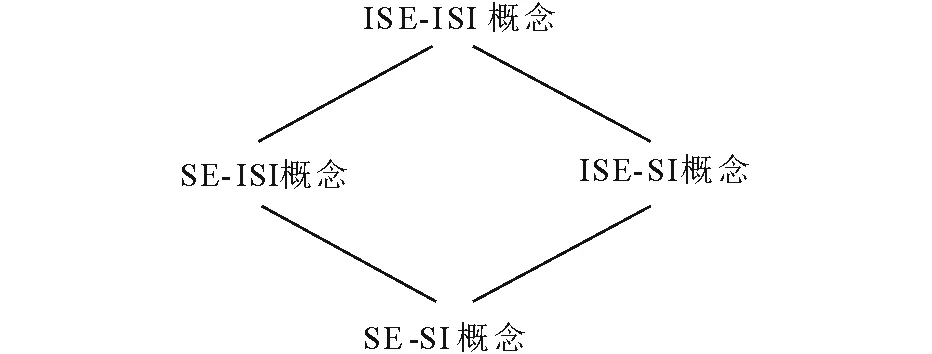
图4 四种部分已知概念Fig.4 Four types of partially-known concepts

SE-ISI 概念最初由Li等[42]提出,其外延是经典集合,而内涵是区间集,表示从外延出发,对概念涵盖的对象有精准的认知,对内涵却只了解大概。而ISE-SI 概念则与之相反,强调的是从内涵的角度去认知,对内涵的把握是准确的,得到的外延只是大概的了解,所以内涵是精确集而外延是区间集。最精确的概念莫过于SE-SI 概念,无论外延还是内涵,都是精确的,二者之间有强烈的依赖关系,相互反映相关信息。形式概念就是SE-SI 概念最好的例子。而最粗略的概念当属ISE-ISI 概念,无论外延还是内涵,都是不够精确的,需要用区间集来刻画。

图5与图6分别是表2所示不完备背景的SE-ISI概念形成的概念格以及ISE-SI概念形成的概念格。

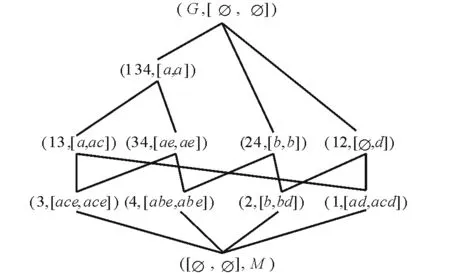
图5 表2的SE-ISI概念格Fig.5 The SE-ISI concept lattice of Tab. 2

图6 表2的ISE-SI概念格Fig.6 The ISE-SI concept lattice of Tab. 2

Li等[43]基于三支决策理论,在不完备背景下建立近似概念,并研究不完备背景下的属性约简,以达到简化近似概念格的目的。

Zhi等[44]将三支概念分析的思想与部分已知形式概念相结合,提出了近似三支概念分析,分别介绍了近似对象导出和属性导出的三支概念格,并研究了它们之间的关系。

王振等[45-46]讨论了不完备形式背景上的4种约简,给出了基于差别矩阵与差别函数计算约简的方法,并研究了它们的关系。

3.1.7 应用

1)冲突分析问题的解决方法

冲突普遍地存在于生活中。在冲突情境中,若能制定合理的方案,则可在很大程度上将损失降到最小,从而使多方获利,否则可能使情况恶化。因此,客观地分析冲突问题,进而做出合理的决策显得尤为重要。由于冲突问题中“同意、反对和中立”这3种态度与三支决策理论的“三分”思想相吻合,所以可以将三支决策理论引入到冲突分析问题中。而三支概念分析不仅蕴含了三支决策的思想,还有可视化的格结构帮助我们从冲突表获取更多知识。

Yao[47]针对冲突分析问题,通过对Pawlak模型的重新构造和扩展,以三支决策理论的哲学、方法论及思维机制为基础,提出了一种三支冲突分析模型,对三分的代理人组进行研究,提出了强冲突、弱冲突和无冲突3个层次的冲突。该模型阐明了冲突的概念和语义解释,并消除了Pawlak模型中存在的不一致性。Fan等[48]通过引入包含度,在冲突表上基于三支决策的思想定义了两对评价函数,利用其取值将代理人集和议题集分别划分成3组,得到一个有效且符合认知的三分模型,可用于制定策略。

2)其他应用

Singh及Subramanian等将三支概念分析广泛应用于多个领域。在医疗诊断方面,Singh等[49]利用基于单值中智图的概念格的性质对医疗数据集进行分析;在访问控制领域, Subramanian等[50]提出了一种基于3WCA的RBAC建模方法。

王立亚等[51]提出了区间三支决策空间概念,通过降低决策损失实现决策的动态调控从而寻求到最优决策方案,并给出医疗诊断实例。

3.2 3WCA文献概况

在前文介绍3WCA成果的基础上,我们对3WCA相关论文进行综合分析。

截止2019年4月底,我们利用“三支概念”、“三支概念格”、“对象导出三支概念”以及“属性导出三支概念”等关键词对国内文献进行检索,得到相关文献32篇;利用“three-way concept”，“three-way concept lattice”，“object-induced three-way concept”以及“attribute-induced three-way concept”等关键词对国外文献进行检索,得到相关文献24篇。

图7呈现了文章发表类型的分布情况。图8与图9是自2014年3WCA提出以来,各年度相关文献的分布情况。表3是4篇高被引论文的基本信息。

图7 文章发表类型分布Fig.7 Types of published papers

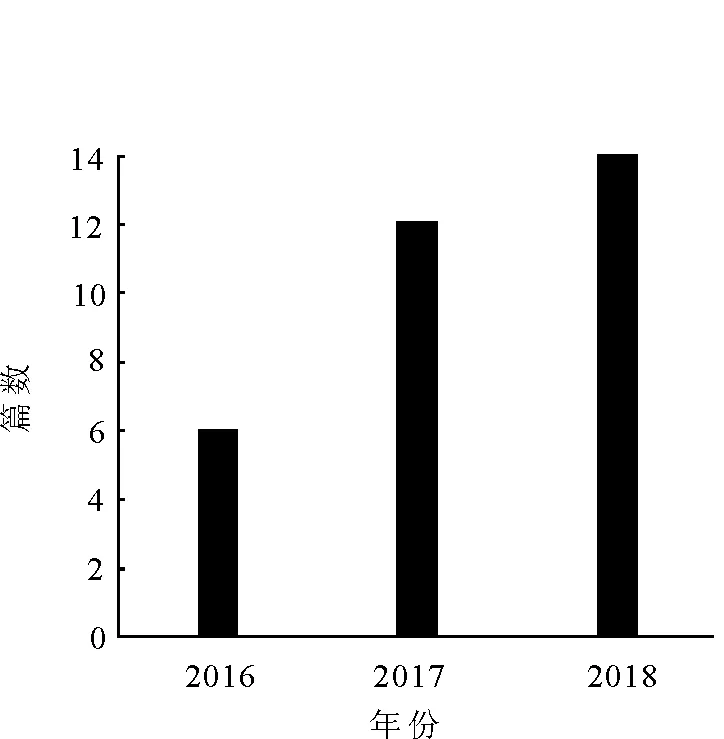
图8 中文文献年代分布Fig.8 Chinese papers published recently

图9 外文文献年代分布Fig.9 Foreign papers published recently

除了上文已提到的专家学者及其所研究的内容之外,还有不少研究团队都在三支概念分析领域做了许多不同方向、不同角度的研究,并取得了不错的成果[52-77]。

4 三支概念分析的研究展望

由于3WCA具有语义详实、可解释性强等特点,在前述研究成果的基础上还有很多可以进一步拓展研究的内容。

4.1 不完备背景的深入研究

相对于完备性的基础信息,不完备的情况在我们的生活和科研领域更为多见。利用部分已知概念这一特殊的三支概念,以及区间集所起的三支作用,可以先从理论上寻求表述和分析不完备背景的方法,探讨不同类型的部分已知概念族的结构,进而应用于实际问题当中。

4.2 决策形式背景的规则获取

FCA中基于决策形式背景进行的规则提取,往往需要设定决策形式背景的协调性。类似地,对于3WCA而言,协调性的设定也是必须的,而且会更为复杂一些,但是其含有的信息也更丰富。由于牵涉到了决策形式背景的补背景及其上的三支规则,也就是负规则的引入,这使得基于决策形式背景的三支角度的规则获取变得复杂,而更有意义。但是这部分工作还没有很好很深刻的成果。

4.3 解决冲突分析问题

文献[47]仅仅对代理人及代理人对进行了三分,类似地,可继续研究对议题和议题对的三分问题,兼顾其中不同的语义解释;还可以分别从代理人集和议题集这两组三分之间的关系进行研究。另外,将冲突表中的“中立”分别视为不确定性态度与确定性态度所产生的不同语义及相关知识发现也将是很有意思的事情。

因此,引入三支概念分析、结合认知科学对冲突问题进行策略制定以及确定冲突情境的核心问题也是未来一个具体的研究方向。

4.4 与三支决策理论的深入结合

三分而治再分析效用,是三支决策理论发展到目前为止较为完全的思想框架[15],而三支概念分析仅利用3WCA中的导出算子考虑了三分,对于治略与效用尚未考虑。即使是三分,目前的研究也多是对完备背景的对象集和属性集进行精确的三分,而对于模糊背景或者不完备背景来说,三分方法的研究是一个非常有意义的问题,而且才刚刚起步。

另外,三分以后,处于边界域中的个体其信息是不够明确的,如何对它们进行更进一步的持续深入的分析,也是不容忽视的问题。Gao等[78]在对三支决策的可行策略进行研究的过程中,通过分析不同域中对象的相似性和差异性,提出了一种动态迁移方案,为边界域中对象给出了一种在不同域之间进行转移的方案。这一思想为三支概念中处于边界域的对象(属性)的进一步分析提供一个新的思路。

因此,这方面的研究工作还大有可为。

表3 高被引论文Tab.3 ESI papers

4.5 粒计算角度

FCA中的粒度和粒层是清晰的[79],3WCA的主体框架是FCA,因此FCA中的粒度与粒层在3WCA中也是可以应用的,但是是否可以有针对3WCA的其他角度的粒描述与粒分析,以及如何将属性粒度的思想引入到不完备形式背景中, 研究相应的区间概念分析,这些都是新问题。

对于L-模糊三支概念格[61]，利用模糊逻辑内在算子, 给出了一种基于剩余格的L-模糊三支概念分析理论,以及基于L-模糊三支概念分析的模糊推理方法, 从而实现了模糊逻辑、三支决策与形式概念分析的有机融合。那么是否可以将该工作在不完备形式背景基础上展开?

另外,关于三支概念在变精度意义下的拓展研究也是尚未开发的领地。

4.6 其他可研究的问题

三支概念虽然语义丰富,但也稍显复杂,因此,探讨其能够表达近似语义、数量不多的近似三支概念以及相应的建格问题和性质,也是很有价值的。

模糊背景为基础的FCA理论成果丰硕,这为探讨模糊背景上的3WCA提供了非常好的研究基础,未来在这个领域的工作必将是深入而丰富的。

与概念认知相关联,三支概念认知学习原则与模型的改进、基于三支概念分析的信息融合与规则学习、以及如何讨论三支概念学习的学习精度等问题,都是很深刻而且有价值的问题。

另外,3WCA中将属性集或者对象集三分的思想来源于三支决策,因此,凡是涉及两极或三支的各种问题,都可以设法用三支概念分析进行建模分析,我们希望能在应用领域具有实际意义的问题中引入三支概念分析。

5 结 语

三支概念分析因为兼具三支决策理论与形式概念分析的优点,也因为其刻画语义的精确性与细致性,使得从认知角度获取新的研究增长点成为可能,从而得到了相关领域范围内学者,特别是国内学者的认可,使其在短短的五年内有了迅速的发展。本文所述研究成果以及未来可行的研究展望,是我们下一步工作的指南。但是,三支概念分析依然存在它不可回避的问题,比如,三支概念格的结构复杂性决定了先建格再获取信息的方法很难具有推广性与适应性,难以在当前大数据潮流下得以应用,这一点与FCA是一样的。因此,有关三支概念分析的研究还需要做很多更深入的工作。