基于粒计算的不确定性分析

苗夺谦，胡声丹

(1.同济大学 计算机科学与技术系，上海 201804； 2.同济大学 嵌入式系统与服务计算教育部重点实验室,上海 201804)

不确定性(uncertainty)是自然界普遍存在的现象,如：玻尔曾指出“不确定性和模糊性是量子世界所固有的”;美籍数学家曼德博针对“英国海岸线有多长”这一问题,给出的答案是“不确定的”;美国气象学家洛仑兹总结提出“蝴蝶效应”以说明系统对初值的敏感性;德国物理学家海森堡提出的“不确定性原理”等。

不确定性也是人类认知过程中普遍存在的现象,当人们用概念、符号、语言、模型等来描述客观世界时,获得的认知具有不完备性或模糊性。同时,不同认知主体受生活经历、知识水平、价值观念、思维方式、兴趣爱好等诸多因素的影响,其认知结构是不同的,所以在感受、认知的过程中,对同一事物的认知是存在差异的。

作为计算机科学的前沿领域,人工智能目标之一是使机器具有人类的智能,并能像人类一样对客观世界进行感知、认知、推理及决策。然而,客观系统存在随机性,人类认知存在模糊性,并且现有知识常常是不完整、不一致的,这一切都要求人工智能对不确定性问题展开深入研究,探索其度量、推理和决策的方法[1]。人工智能领域多年来对不确定性问题的探索推动了粒计算理论的兴起和发展。粒计算是一种新的计算范式,它以多粒度的表示、问题求解方法、信息处理模式等为研究对象,属于人类较高层次认知机理研究的范畴[2]。由于其抽象了人类以多层次、多视角处理问题时所表现出全局观和近似求解能力,粒计算逐渐成为不确定性问题求解的重要理论。在过去的30年中先后涌现出基于模糊集[3]的词计算[4]、粗糙集[5]、商空间[6]、云模型[1]等经典粒计算理论模型,粒计算的应用领域包括大数据分析与挖掘、知识发现、模式识别、聚类分析、复杂问题求解等。

1 粒计算理论

1.1 粒计算的发展历程

美国数学家、控制论专家L.A.Zadeh教授指出，Cantor集合论为了达到精确和严格的目的,将思维过程绝对化,而现实世界中复杂事物不可能绝对精确,存在着大量模糊现象。于是在1965年提出模糊集合论,其主要思想是使用“隶属函数”对“属于”或“不属于”之间的过渡状态进行量化,对经典集合论进行推广。

在模糊集的基础上,Zadeh于1979年首次提出并讨论了模糊信息粒度化问题[7]。他认为，信息粒的概念存在于很多领域中,如自动机与系统论中的“分解与划分”、区间分析里的“区间数运算”等。美国Stanford大学J.R. Hobbs教授于1985年,发表了题为“Granularity”的论文[8],讨论了粒的分解与合并,提出了产生不同大小粒的模型和方法。1996年,T.Y. Lin教授在加州大学伯克利分校访问时,向Zadeh提出了“Granular Computing”(粒计算,缩写为GrC)的研究,至此,粒计算一词正式诞生。随后,他发表了关于粒计算的论文[9],讨论了二元关系下的粒计算模型,论述了粒结构、粒表示、粒应用等方面的问题。1996年,Zadeh提出“词计算理论”[4],标志着模糊粒度化理论的诞生。在Lin的工作基础上,加拿大里贾纳大学的Y. Y. Yao教授于1999年提出了基于邻域系统的粒度计算模型,对粒度计算进行了研究[10],并将它应用于知识挖掘等领域,建立概念之间的IF-THEN规则与粒度集合之间的包含关系,提出利用由所有划分构成的格求解一致分类问题,为知识挖掘提供了新方法和视角。

在国内,张钹院士和张铃教授于1990年提出了基于商空间的粒度计算模型[6]。商空间理论用商集表示不同的粒度层次,建立不同粒度世界之间的保真、保假原理。该理论通过观察当前粒度空间是否可解,来决定是否进入更细、更深的粒度空间,将不同粗细的粒世界上的粒的解组合成原问题的解,并提出一种商粒度空间上的多粒度表示法,构建多粒度的分层递阶商空间结构。20世纪末,李德毅院士在概率论和模糊数学理论基础上,提出了云模型,通过赋予样本点以随机确定度来统一刻画概念中的随机性、模糊性及其关联性。基于云模型的云变换可以实现不同粒度层次上概念的合成和分解,是一种可变粒计算[1]。进入21世纪后,粒计算的研究在国内受到越来越多学者的关注。刘清教授在他的专著中阐述了信息粒度及其计算,并将粒度计算的方法成功应用于医疗诊断专家系统[11];苗夺谦教授在研究粗糙集理论时引入信息论,开创性研究了知识的信息表示与信息度量,提出了知识的信息熵、条件熵和互信息等概念,分析讨论了知识的不确定性(粗糙性)与信息熵之间的关系[12-14],并用粒计算的概念阐述了对不确定性的研究[15];王国胤教授等探讨了模糊集、粗糙集、商空间理论模型及其他扩展粒计算模型中知识的不确定问题[16];梁吉业教授等研究了信息系统中信息粒的刻画和表示,建立了信息粒度与熵之间的互补关系[17];吴伟志教授等讨论了概念格中的粒度结构,并应用到形式概念分析中[18]。近年来,国内学者张燕平[19]、钱宇华[20]、李天瑞[21]、张贤勇[22]等关于粒计算研究的论文相继发表。

1.2 粒计算主要模型

张钹院士、张铃教授指出“人类智能的一个公认特点,就是人们能从极不相同的粒度上观察和分析同一问题。人们不仅能在不同的粒度世界上进行问题的求解,而且能够很快地从一个粒度世界跳到另一个粒度世界,往返自如,毫无困难”[6]。粒计算正是反映了人类这种多层次、多视角的处理问题方式,逐渐成为不确定性问题求解的重要理论。粒计算的基本模型如图1所示,包括粒结构、粒层、粒子三部分,从不同视角看待问题可以构建不同的粒结构,一个粒结构由多个粒层构成,每个粒层又由多个粒子构成,不同粒层的粒子可以通过粗化或细化进行转换。

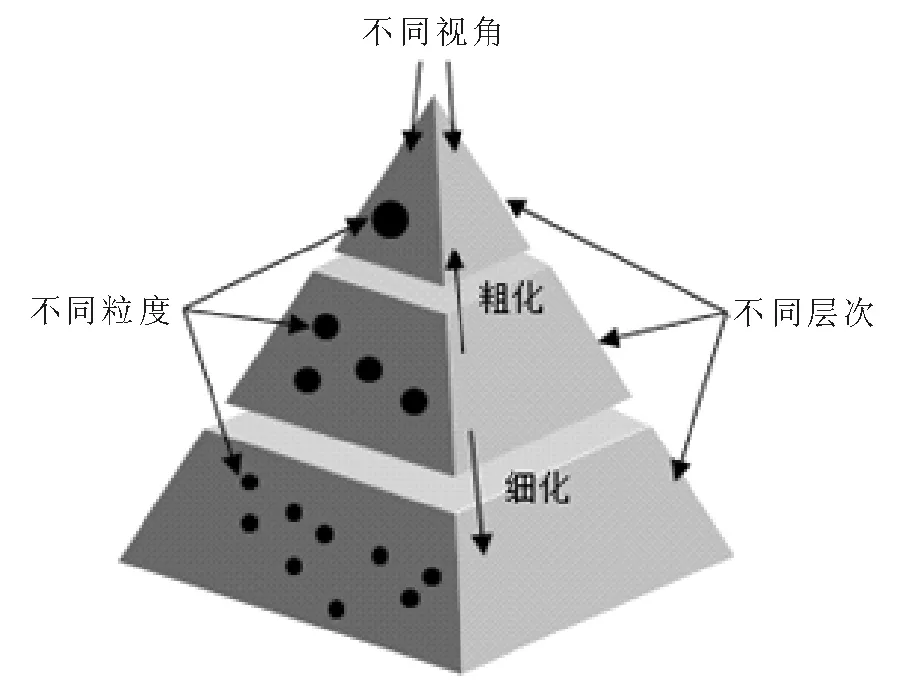
图1 粒计算基本模型Fig.1 A basic model of granular computing

粒计算理论的代表模型有模糊集、粗糙集、商空间、三支决策和云模型等。其中,基于模糊集的词计算模型侧重于信息的模糊粒化,以处理计算对象的不确定性为主要目标,而粗糙集、商空间、三支决策、云模型则侧重于不同粒度上复杂问题的不确定性,以复杂问题的多粒度计算为主要目标。

1)模糊集模型

模糊集合论是通过计算对象关于集合的隶属程度来近似描述不确定性,反映了集合边界的不分明性。

经典模糊集(也称为一型模糊集)中隶属度μA(x)(0≤μA(x)≤1)反应了对象x属于模糊集A的程度。隶属度越小,说明x属于A的程度越低;隶属度越大,说明x属于A的程度越高。当μA(x)={0,1}时,模糊集退化为经典的精确集。该模型中隶属度值是精确唯一的,后续研究中出现了对经典模糊集的各种扩展模型,如区间值模糊集、直觉模糊集、二型模糊集、Vague集、勾股模糊集等。

对信息的模糊粒化,使得计算机能够在不精确以及部分精确的环境下给出合理的决策成为可能。随着模糊集理论的不断发展完善,以模糊逻辑和信息粒化为基础的模糊信息粒化理论能进一步发展,并为词计算的发展提供了前提条件。

2)粗糙集模型

粗糙集理论[5]由波兰科学院院士Pawlak于1982年提出,它是一种处理不精确、不一致和不确定性知识的数学工具。粗糙集模型的基本思想是利用不可分辨关系(等价关系)构成对象的等价类,所有的等价类构成论域的划分,从而建立一个近似空间。对于任意概念(集合),可以利用近似空间中的一对精确概念(集合)(下近似集和上近似集)来表示,从而建立概念(集合)的边界定义。

定义1设信息系统IS=(U,A,V,f)中,对∀X⊆U,R⊆A,概念X关于知识R的下近似和上近似分别定义为:

则X的R正域、负域和边界域分别为:

即X的R正域由那些根据知识R判断肯定属于X的元素组成;负域由那些根据知识R判断肯定不属于X的元素组成;边界域由那些根据知识R既不能判断肯定属于X、又不能判断肯定不属于X的元素组成。

经典粗糙集模型定义在等价关系的基础之上,针对只包含符号型数据的完备信息系统,使用精确的集合进行概念的表示及知识的获取。但在实际问题求解过程中,等价关系、符号数据、完备系统、精确的上下近似集等要求过于严苛,众多学者对经典粗糙集进行扩展,提出了适应不同问题的扩展粗糙集模型,包括粗糙模糊集和模糊粗糙集[23],层次粗糙集[24]、多粒度粗糙集[20]、多尺度粗糙集[25]等。

3)商空间模型

我国学者张钹院士和张玲教授在研究问题求解时,独立地提出了商空间理论[6],将不同的粒度世界与数学上的商集概念统一起来。根据研究目的的不同,商空间理论对同一问题可以构造不同的商空间,从而得到原问题不同角度、不同层次的解,最后综合这些解构成原问题的解。

商空间理论中,由等价关系产生论域X的不同商集[X]及其对应的商空间([X],[f],[T])构成了原问题(X,f,T)的不同粒度世界。分层递阶商空间链可以表示问题的不同粒度空间,利用商空间的保真、保假原理,建立不同粒度空间之间的联系,在不同的粒度世界上进行推理,从而简化问题和加快问题求解的速度。

对商空间理论进行的推广,包括引入模糊等价关系[26]、模糊相容关系[27]等。

4)三支决策模型

三支决策是在传统的“接受”、“拒绝”二支决策选项基础上加入“不承诺”选项,可以有效地规避对象认知不确定情况下误接受或误拒绝所造成的损失。同时,对不承诺项的再研究,可细化对决策对象的认知粒度,进而提高决策的准确性[28]。

加拿大学者Y. Y. Yao教授将三支决策思想引入到概率粗糙集中,提出决策粗糙集模型,该模型使用一对阈值(α,β)(0≤β<α≤1)来决定正域、负域和边界域,并将正域、负域和边界域分别解释为接受、拒绝和不承诺3种决策。其中,阈值的选取是关键,可以由损失函数λ决定,而λ的大小由实验或专家给出。

近年来,越来越多的学者研究和拓展了三支决策理论、方法,并将其应用到多个研究领域,如三支决策空间[29]、决策规则冲突[30]、流计算[31]、属性约简[32]、情感分类[33]等。

5)云模型

云模型是由我国学者李德毅院士在概率论和模糊数学理论基础上,提出的定性定量转换的认知模型[1],它可以实现定性概念与定量数值之间的双向转换。云模型通过赋予样本点随机确定度来统一刻画概念的随机性、模糊性及其关联性,利用期望、熵、超熵3个数字特征来整体表征一个定性概念,并通过正向云发生器、逆向云发生器算法形成定性概念与其定量表示之间的不确定性转换。

云模型中云滴x对定性概念C的确定度μ(x)是具有稳定倾向的随机数,是论域U到区间[0,1]上的概率分布,而不是一个固定的数值。云滴的确定度可以理解为云滴能够代表该定性概念的程度。云滴出现的概率越大,云滴的确定度越大,则云滴对概念的贡献越大。

云变换是通过高斯混合模型和逆向云发生器,对样本数据的分布进行拟合,抽取形成不同粒度的多个概念,随着粒度的提升,细粒度的概念可以通过概念爬升形成新的更大粒度的概念。基于云模型的粒计算本质上是基于概率统计的方法实现粒计算和可变粒计算。

2 粒计算理论与不确定性分析

对不确定性问题的研究,主要包括不确定性问题的描述、不确定性的度量、不确定性推理等。针对模糊集、粗糙集、商空间、三支决策、云模型5个粒计算理论模型,不确定性研究的主要内容概括起来如表1所示。

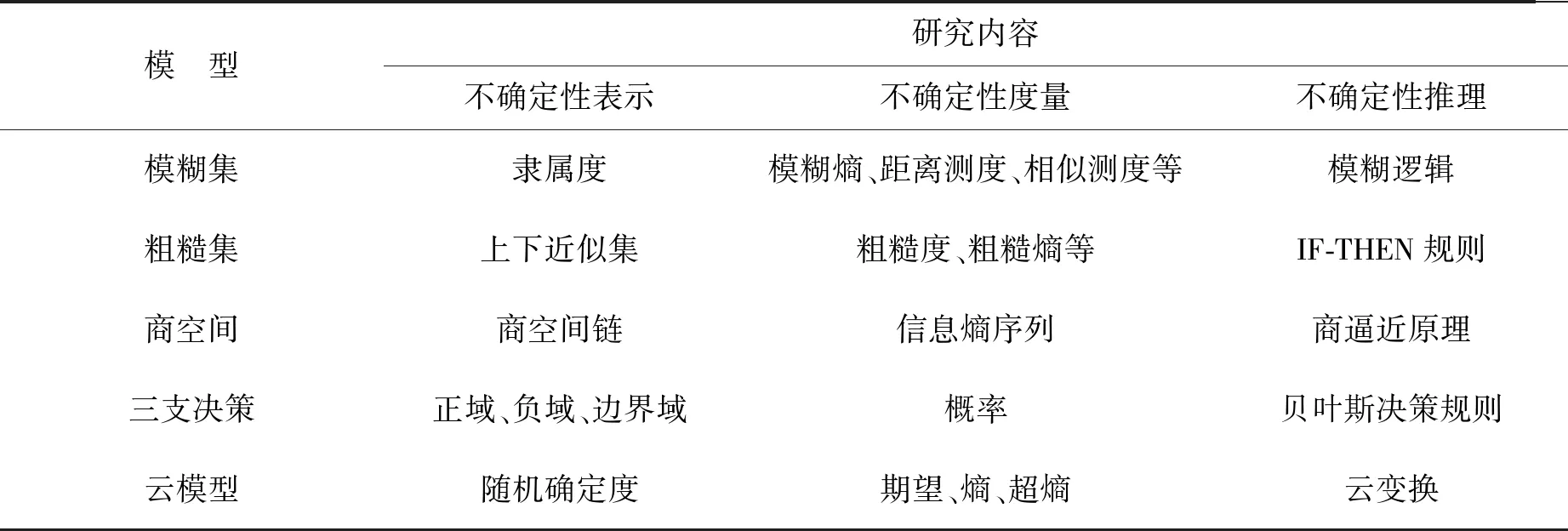
表1 粒计算主要模型与不确定性研究内容Tab.1 Research contents in some granular computing models

其中,在粗糙集理论中,将知识视为关于论域的划分,且知识是有粒度的。概念的不确定性用概念相对于知识的上下近似集合来描述;对概念、知识的不确定性度量方式有代数方法下定义的精度[34]:

粗糙度[34]:

ρR(X)=1-αR(X),

信息方法下定义的粗糙熵[35]:

知识Q相对于知识P的条件熵[13]:

H(Q|P)=

互信息[13]:

I(P;Q)=H(Q)-H(Q|P),

互补熵[36]、Rough熵[36]等;使用从条件集到决策集的IF-THEN规则进行不确定性推理,以获取知识。

3 基于粗糙集模型的不确定性分析

粒计算研究内容主要包括：问题的粒化,即如何构建粒的结构;粒的度量,即如何衡量粒子的“大小”或“粗细”;粒算子,即基于粒与粒之间的关系,如何构造粒的运算、粒的转换等[2]。在粗糙集背景下,从粒的表示、粒的度量、粒的关系及转换、属性约简与规则提取等方面分析不确定性。

3.1 多粒度

经典粗糙集理论中,论域中的任意概念可以用等价类[x]R近似表示,每个等价类被看成一个知识粒,粒内部的各元素间具有不可分辨关系,所有的知识粒形成论域的一个划分。使用一个属性集对全域进行等价划分形成信息粒,由这些信息粒构成的模型被称为单粒度粗糙集模型。

以单粒度粗糙集模型为基础的多粒度粗糙集模型可以发掘不同粒度之间的关系,对单粒度的信息进行融合,进而在多粒度下进行约简与知识获取,引起了众多学者的关注。其中苗夺谦、冯琴荣等[24]在分析人类先验知识结构化特点之后,从属性值域出发,将每个属性扩展成一个概念层次树,提出了一个粗糙集的扩展模型,即层次粗糙集模型,并应用于层次决策规则挖掘。基于层次粗糙集模型,钱进[37]等提出了大数据下层次决策规则并行计算模型,用于大数据背景下不同层次决策规则的挖掘。苗夺谦、张贤勇等[22]提出双量化粗糙集模型,对概率粗糙集和程度粗糙集进行了扩展,并从粒计算角度分析了4种剖分区域的特点,研究了基于逻辑或的双量化粗糙集模型的属性约简、基于重要度准确率的粒构造和属性约简[38]。钱宇华等[20]分析了在多源信息系统、高维特征数据集、多智能体等应用中单粒度粗糙数据分析方法的局限性,提出了基于“求同存异”策略的乐观多粒度粗糙集和基于“求同排异”策略的悲观多粒度粗糙集,苗夺谦、刘财辉等提出了多粒度覆盖粗糙集[39]、多粒度覆盖粗糙模糊集[40]。此外,典型的多粒度粗糙集模型还有吴伟志等提出的多尺度粗糙集[25]。

3.2 粒的度量

粗糙集理论中,等价类是信息系统的基本知识粒,知识粒度是知识粒的一种平均度量,反映了知识的分类能力,粒度越细,分类能力越强。苗夺谦、范世栋等[15]给出了知识库中知识粒的度量,并从知识粒度:

知识分辨度:

Dis(R)=1-GD(R),

知识熵:

的关系上研究了粗糙集的不确定性。冯琴荣、苗夺谦等在文献[41]中定义了知识的划分粒度

来度量知识的分类能力。

不同粒层的知识粒度之间存在粗细关系,知识粒度随知识划分能力的增强而减小,而同一粒层下知识的分辨能力与粒度存在互补关系,而知识熵随知识粒度的减小而单调递增。事实上,知识的划分粒度可以看成是期望粒度,是对知识导出的划分中各划分粒“平均”长度的一种度量,它的值越小,表明划分粒的平均长度越短,论域中划分粒的个数就越多,即该知识能区分开的对象就越多,因此分类能力也就越强,不确定性越小。

关于知识粒度,刘财辉等在文献[42]中对几种度量方法进行了比较研究,详细分析了它们之间的联系与区别。

3.3 粒的关系

粗糙集模型中,从不同角度、不同层次看待对象集、属性集、属性值集,能形成不同的粒结构、粒层及粒子,不同层的粒子之间存在粗细关系。

1)属性集变化与粒度的关系

定义2设P,Q是论域U上的两个等价关系,且U/P={X1,X2,…,Xn},U/Q={Y1,Y2,…,Ym},如果对任意Xi∈P,存在Yj∈Q,使得Xi⊆Yj,称U/P是比U/Q更细的划分,记为P≼Q。

若P≼Q,则有GD(P)≤GD(Q),Dis(P)≥Dis(Q),H(P)≥H(Q),E(P)≤E(Q)成立。

通过改变属性集中属性的个数也会引起粒度的变化,若属性集P，Q满足P⊆Q,即在属性集P上增加属性得到属性集Q,则由知识Q形成的划分更细,划分空间中的粒子个数增加,粒子变细,知识粒度变小,即GD(P)≥GD(Q)成立。

以UCI数据集Molecular Biology (Splice)(3190个对象,60个条件属性)为例,当属性集R属性编号分别为{1},{1,2},…，{1,2,…,10}时,知识划分的不确定性与属性集之间的变化关系如图2所示,即说明了随着属性集R属性的增加,知识的划分越细,粒子越细,知识粒度GD(R)越小,分辨度Dis(R)越大,知识熵H(R)越大,知识的划分粒度E(R)越小,不确定程度越小。

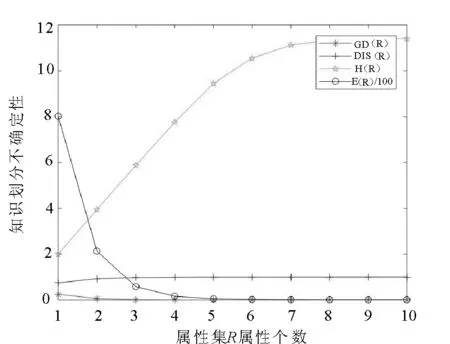
图2 属性集属性个数与知识划分不确定性Fig.2 Relations between the number of attributes and uncertainty of knowlege

2)属性值变化与粒度的关系

层次粗糙集模型[24]中,属性在不同概念层具有不同的值域,属性值域的变化也会引起粒度的变化。

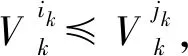
针对文献[24]数据表,选取属性集R={education-level},基于属性集的不同概念层,数据的划分U/R及不确性度量结果如表2所示。

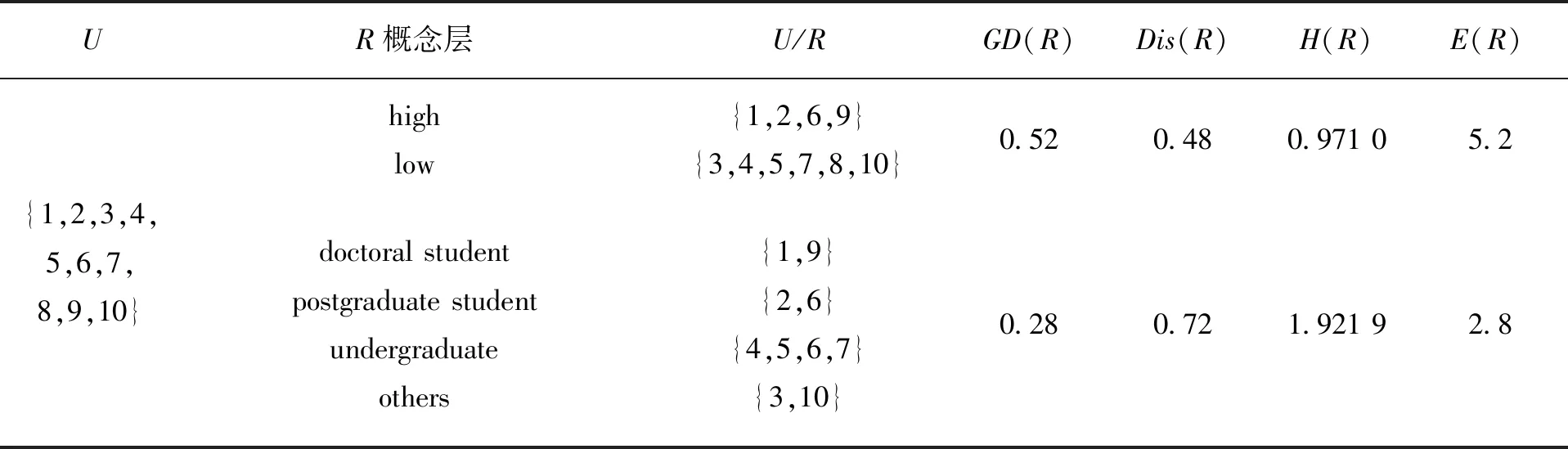
表2 属性集概念层与知识划分不确定性Tab.2 Relations between the concept hierarchies of attributes and uncertainty of knowledge

从表2可以看出,对于某个属性集,其值域越细,该概念层对应的等价关系划分能力越强,粒子越细,知识粒度越小,不确定性越小。

3.4 知识约简与规则提取

粗糙集理论的一个重要任务是在决策表中获取知识,而这种知识通常是用规则形式表示的,决策表的每一行即确定一条决策规则,而利用决策表信息提取规则并进行智能处理之前,需要利用某一标准对信息系统进行知识约简[43]。

知识约简是指删除条件属性集中冗余的属性或属性值后,能保持原始决策表条件属性与决策属性之间的依赖关系,即约简后的属性子集是对论域的划分空间保持不变的前提下的最粗划分。约简算法可以通过删除冗余属性或添加重要属性进行,其中添加属性的方式是从信息系统的核开始,按照一定的启发信息获取属性约简[44]。

从粒计算的角度看,条件属性的增加或删除会改变粒空间的知识粒度,删除属性时知识粒度会增大,而添加属性时知识粒度会减小,如图3所示。属性约简的过程本质上是根据知识的变化不断改变粒层和粒子结构的过程,直至得到决策划分空间U/D的最大近似划分。

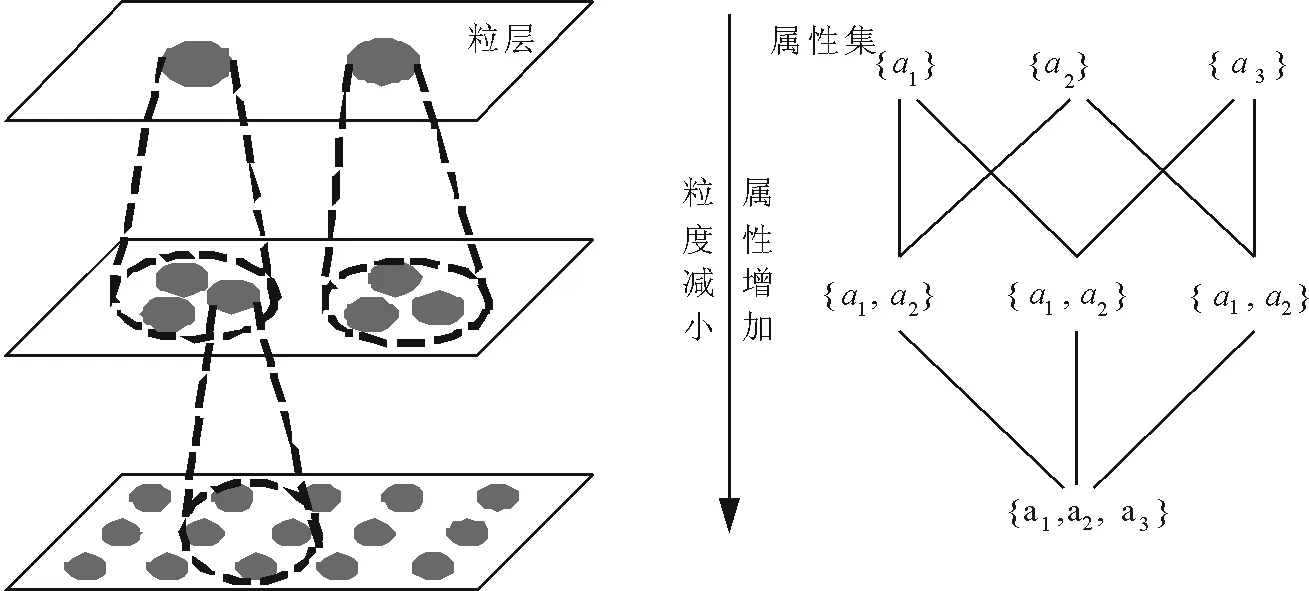
图3 粒层与属性集变化关系Fig.3 Relations between granule level and attributes

决策表中,可以从不同粒层上提取规则,由于粒度的不确定性会引起决策规则的不确定。决策规则C→xD不确定性即反映所表达知识的真实性,其度量方式有确定性因子Cer(C→xD)和覆盖因子Cov(C→xD)[45]。

4 结 语

不确定性是一种普遍存在的现象,广泛存在于自然科学和社会科学领域。粒计算是一种新的计算范式,是研究基于多层次粒结构的思维方式、问题求解方法、信息处理模式及其相关理论、技术和工具的学科,由于其反应了人类处理具有多层次、多视角问题时体现的全局观和近似求解能力,粒计算逐渐成为不确定性问题求解的重要理论。

虽然粒计算针对不确定性问题在理论模型、应用方面取得了大量研究成果,但还存在以下问题有待深入研究:能否或者如何整合模糊集、粗糙集、商空间、云模型等模型的优点,构建统一的粒计算模型?针对问题空间,如何构建合理的粒结构、粒层、粒子,并在问题求解时,在多粒度空间下选取最合适的粒度?不同粒层的粒子转换算子如何构造,以及粒转换过程中的不确定性如何度量?