基于梁体转角的高速铁路桥梁挠度测试方法研究

2019-07-22王巍姚京川刘鹏辉杨宜谦董振升孟鑫尹京

中国铁路 2019年7期

王巍，姚京川，刘鹏辉，杨宜谦，董振升，孟鑫，尹京

（1.中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081；2.中国铁道科学研究院集团有限公司高速铁路轨道技术国家重点实验室，北京 100081）

1 概述

高速铁路为节约用地，多采用以桥代路的形式，从目前运营和在建的高速铁路看，桥梁占线路比例高，部分线路桥梁比例达82%[1-4]，为满足跨越大江、公路和河流需要，许多大跨度的新型特殊结构桥梁被采用，如连续钢桁梁、斜拉桥等。高速铁路桥梁设计主要受刚度控制，基本上不受强度控制。在桥梁刚度控制方面，为满足高速行车条件下的行车安全和乘坐舒适要求，国内外规范多以设计荷载作用下的挠度作为限值指标[5-6]。

传统挠度测试方法以接触式测量为主，适用于桥下可搭设支架的桥梁挠度测试，其成本较低；对于桥下跨越江河和峡谷等桥梁挠度的检测，多采用CCD图像法，但CCD图像法随着距离的增大，其精度逐渐降低。倾角仪为桥梁挠度测量提供了一种新手段，利用倾角仪测量桥梁截面转角以拟合桥梁挠度，不需要静止的参考点，且具有很高的精度。

杨学山等[7-8]提出采用一组基函数的线性组合来拟合桥梁结构的挠曲函数，但受限于基函数的影响，该方法仅适用于刚度变化较小的等截面结构，对于刚度变化复杂的桥梁，测试结果误差很大。杨小森等[9]提出采用桥梁结构的自振振型作为基函数来拟合桥梁结构的挠曲函数，但文献中的振型函数需要采用精确的有限元模型求解计算，若桥梁结构出现损伤或经过加固后，需及时更新有限元模型。

针对上述问题，文献[10]提出简化振型函数方法，适应于各种复杂多变的桥梁结构形式的基于转角的桥梁挠度测试。以下对文献[10]的简化振型函数方法进行有限元模型验证，并建立包含数据采集和分析的测试系统，通过现场试验验证这一方法的有效性。

2 有限元模型验证

我国高速铁路桥梁梁型主要以32 m简支梁为主，在跨越山谷、河流、铁路、道路等情况下会采用大跨度连续梁、斜拉桥等特殊结构。分别选取简支箱梁、连续箱梁和斜拉桥进行有限元模型的验证，利用Midas软件建立了桥梁的有限元模型，采用CRH2动车组列车单线加载，轴重12.5 t，轴距为2.5 m，转向架中心距17.5 m，车长25 m，8节编组，不计动车组列车的动力效应，只考虑静荷载作用。

2.1 简支箱梁

假定倾角仪等间距布置于某高速铁路32 m简支箱梁上，分别选择3阶、4阶、5阶、6阶模态，采用文献[10]所述方法，利用简支箱梁跨中竖向挠度最大时有限元节点的转角值拟合桥梁跨中竖向挠度，拟合结果见表1，采用节点转角拟合的桥梁挠度曲线与有限元计算的对比见图1。

表1 简支箱梁不同模态阶数下的跨中节点挠度

图1 简支箱梁不同模态阶数时转角拟合的桥梁挠度与有限元计算结果对比

可以看出，采用不同阶数模态拟合桥梁跨中竖向挠度的最大值略小于有限元计算结果，各个组合下的相对误差均小于5%。从表1中可以看出，不同阶模态拟合的结果基本相当；利用5个节点测试拟合的结果能够满足工程上的要求，相对于7个节点测试，布置的倾角仪更少，降低了现场试验的工作量和试验成本。因此，对于常用跨度简支梁，采用3阶或4阶模态、选择5个节点布置倾角仪的测试拟合方式即可得到桥梁挠度测量满意的结果。

2.2 连续箱梁

假定倾角仪等间距布置于某高速铁路（40+64+40）m预应力混凝土连续箱梁64 m中跨上，分别选择3阶、4阶、5阶、6阶模态，采用文献[10]所述方法，利用64 m中跨跨中竖向挠度最大时有限元节点的转角值拟合桥梁跨中竖向挠度，拟合结果见表2，采用节点转角拟合的桥梁挠度曲线与有限元计算的对比见图2。

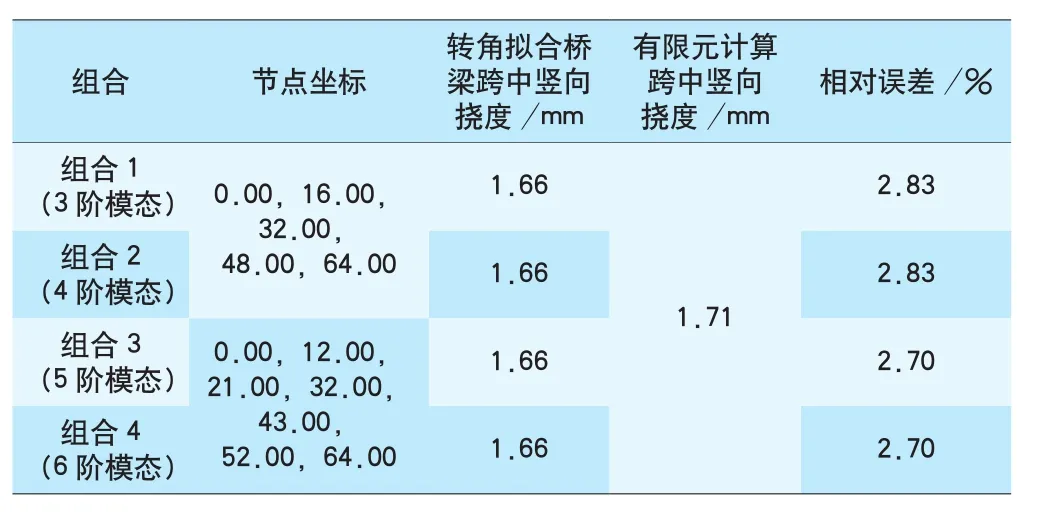
表2 连续箱梁不同模态阶数下的跨中节点挠度

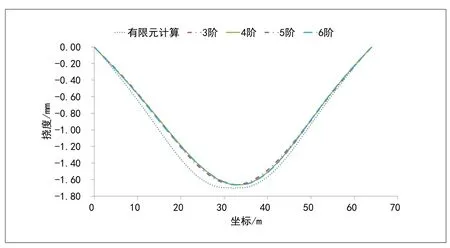
图2 连续箱梁不同模态阶数时转角拟合的桥梁挠度与有限元计算结果对比

对比看出，采用不同阶数模态拟合桥梁跨中竖向挠度的最大值略小于有限元计算结果，各个组合下的相对误差均小于5%。因此，对于常用跨度连续箱梁，同样采用3阶或4阶模态、选择5个节点布置倾角仪的测试拟合方式即可得到桥梁挠度测量满意的结果。

2.3 斜拉桥

假定倾角仪等间距布置于某高速铁路（120+5×168+120）m的六塔连续钢桁结合梁斜拉桥168 m跨（第4孔）下行侧下弦杆上，CRH2动车组列车的加载轮位见图3。分别选择3阶、4阶、5阶、6阶模态，采用文献[10]所述方法，利用168 m跨（第4孔）下行侧下弦杆跨中竖向挠度最大时有限元节点的转角值拟合桥梁跨中竖向挠度，拟合结果见表3，采用节点转角拟合的桥梁挠度曲线与有限元计算的对比见图4。

图3 CRH2动车组列车加载轮位

表3 斜拉桥不同模态阶数下的跨中节点挠度

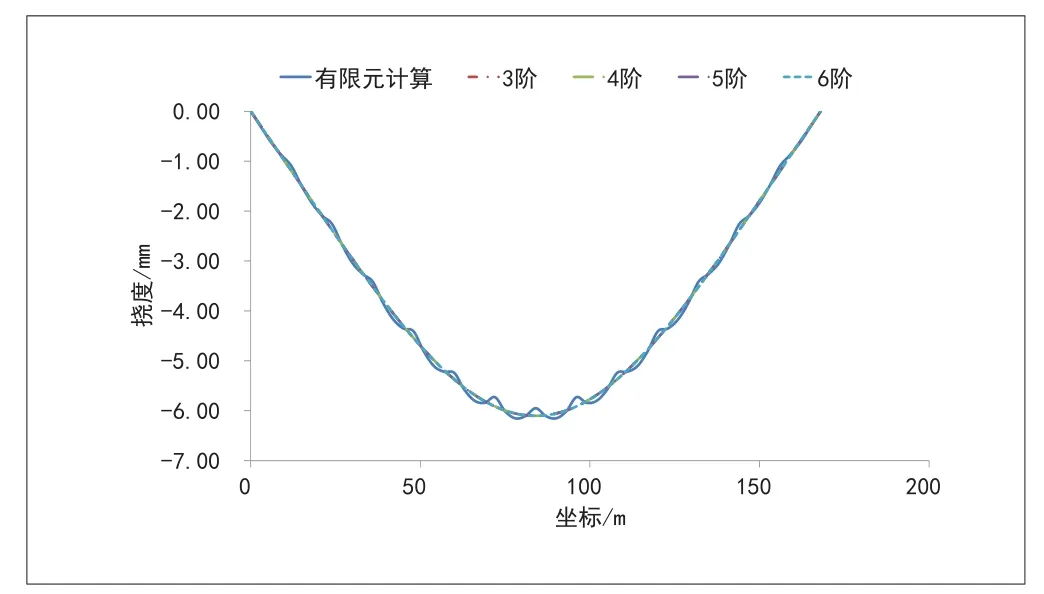
图4 斜拉桥不同模态阶数时转角拟合的桥梁挠度与有限元计算结果对比

采用不同阶数的模态拟合桥梁跨中下弦杆竖向挠度的最大值略大于有限元计算结果，各个组合下的相对误差均小于5%。因此，对于钢桁梁斜拉桥，采用3阶或4阶模态、选择5个节点布置倾角仪的测试拟合方式也可得到桥梁挠度测量满意的结果。

综上所述，采用文献[10]的简化振型函数方法拟合桥梁挠度能够满足工程上的要求，且可以实现桥梁单跨多点挠度的同步测试；简化振型与梁型无关，只与桥梁跨度有关。对于不同梁型，一般采用4阶模态、5个节点布置倾角仪的测试拟合方式即可得到理想桥梁挠度测量的结果，相对误差均小于5%，倾角仪宜等间距布置在简化振型函数极值点的位置处。

3 测试系统的建立和试验验证

3.1 测试系统的建立

测试系统是获取各种传感器和其他待测设备等模拟和数字被测单元中的信息，然后对采集到的数字化信息进行处理得到信号代表的物理意义，最后进行数据分析与科学研究的系统。完整的测试系统由前端数据采集软件与硬件设备、后端数据处理与分析软件组成。

需建立的测试系统中的前端传感器特指倾角仪，通过对倾角仪传感器量程、精度、灵敏度、横向灵敏度、频率范围、线性范围、相移特性、分辨率、零位漂移和使用环境等的对比分析，最终选定QY型倾角仪作为前端传感器。试验前，将QY型倾角仪等间距布置于梁上，QY型倾角仪输出的模拟电信号可以通过导线传输给采集设备，采集设备将模拟信号转换成计算机可识别的数字信号，并通过数据采集软件进行简单的处理，转换成可供外部软件读取的数据格式。此测试系统不受桥梁跨度和地形的影响，可以用来测试跨越江河和峡谷等桥下不能布置传感器的大跨度桥梁准静态挠度，测试系统适用性强。

基于文献[10]提出的简化振型函数方法，设计编制数据分析软件，编制的数据分析软件主界面及计算分析见图5。

图5 测试系统数据分析软件主界面及计算分析

3.2 试验验证

分别选取高速铁路32 m简支箱梁、（40+2×64+40）m连续箱梁进行了现场试验，在箱梁底板等间距布置5个QY型倾角仪，测试动车组列车准静态通过时梁体跨中竖向挠度，并采用差动式位移计悬锤法进行对比测试，倾角仪和差动式位移计悬锤法测试见图6。

同时，选择跨越江河的（126+196+126）m下承式连续钢桁梁、（81+135+432+135+81）m钢桁梁斜拉桥进行现场试验，在测试孔跨下弦杆等间距布置5个QY型倾角仪，测试动车组列车准静态通过时桥梁跨中竖向挠度，并采用静载试验的水准仪或激光多普勒非接触测量结果进行对比测试。（126+196+126）m下承式连续钢桁梁、（81+135+432+135+81）m钢桁梁斜拉桥现场情况见图7和图8。

图8 （81+135+432+135+81）m钢桁梁斜拉桥

动车组列车以5 km/h准静态通过时，跨中准静态挠度的响应频率较低，一般为0.1 Hz以下，测试中可对倾角仪信号进行低通滤波剔除干扰信号，（40+2×64+40）m连续梁64 m跨中不同位置的倾角仪时域图（1 Hz低通数字滤波后）见图9。动车组列车以5 km/h准静态通过时，32 m简支箱梁、（40+2×64+40）m连续箱梁、（81+135+432+135+81）m钢桁梁斜拉桥时，采用倾角仪与对比测试方法得到的时域波形（低通1 Hz）见图10—图12。1 Hz低通数字滤波后，不同桥梁倾角仪拟合的跨中竖向挠度与其他测试方法的对比见表4。