浅谈数学中的美
2019-07-21代莉
代莉
(重庆市綦江职业教育中心,重庆 401420)
什么是美?自古以来,人类从来没有停止过对美的学习,而且对“美是什么?”都有不同的衡量标准和价值取向,见者见智。那到底什么是美呢?俗话说:“爱美之心,人皆有之。”著名的李泽厚大师曾说过:“完好、和谐、鲜明、真与善、规律性与目的性的统一,就是美的本质和根源”。
一、数学中的符号美
据我观察,“惰性”无论是在自然界,还是在人类的世界都受到我们的热烈追捧,只要能够偷懒,能够简洁,我们就绝不会去“多此一举”:光沿直线方向传播,这是因为它是最为便捷的距离;大雁迁徙时呈人字飞行,这是由于他们所受到得阻力最小;在人体中,人的粗细血管之比是这又是缘于它在疏导液体时能量消耗得最少……这些都向我们展示了万事万物的简洁与和谐。宇宙万物都是如此,那数学更不用说了。法国哲学家狄德说道:数学中所谓美的回答,是关于困难而繁杂的题目的简单回复。事实上,数学的简单是体现在简单的语言和求解方法简单。数学,不喜欢笨拙和复杂。
那现在我们就来看看数学符号吧!数学符号的首要在于它存在无限的气力和门径来协助直觉,把自然和社会甚至于宇宙中的数学关联起来,去回答那些已知或未知的问题,去创造更新、更深的思维形式。如:
(一)表示数的符号,如0,1,2,…,8,9这类数字在学习了计数的方法后,我们将使用它们来代表不同的数字。
(二)括号,如(),[],{},等等;通过它,可以对代数符号与符号构成式子(或项),进行组织,使之能形成各种复杂的结构。括号在数学上,特别是代数公式语言的构成上起着十分重要的作用。[5]
(三)语标符号,数学有一些语标符号。这是表示特定的数学对象的符号,其书写形态也 专门为此而“发明”的。大家最熟悉的数字0,1,2,…,9便是语标符号的例子,其他还有+、-、×、÷、,…,等等。
二、数学中的抽象美
万有引力的萌芽,在牛顿之前的历史上早就有存在,但仅仅只有当牛顿通过用数学公式精确的表达时,才成为科学中最有意义、最重要的万有引力定律。爱因斯坦的广义相对论的孕育与发表,也得益于黎曼几何所供应的数学框架和门径。
当数学家的思想变得更抽象时,他会发现使用物理世界来测试他的直觉越来越难。为了确认直觉,他必须更详细地,更小心地下定义和证明,和为了到达更高程度的精确性而进行的连续的努力,这样以来也使得数学本身得以成长了。
数学的简洁性在很大的程度上是源自数学的抽象性,换句话说:数学概念正是从众多事物共同属性中抽象出来的。而对日益扩展的数学知识总体进行简化、廓清和统一化时,抽象更是必不可少的。
如前所述,微积分的创始人牛顿和莱布尼兹分别从力学(研究物体的速度、加速度)和几何学(讨论曲线的切线)不同角度引入建立同一概念、创立同一学科——微分学;而他们又分别从“反运算”和“微分求和”不同角度建立另一门学科——积分学。这也使微分、积分(微积分)成为一个不可分离的整体学科。
同一个拉普拉斯(Laplace)方程:
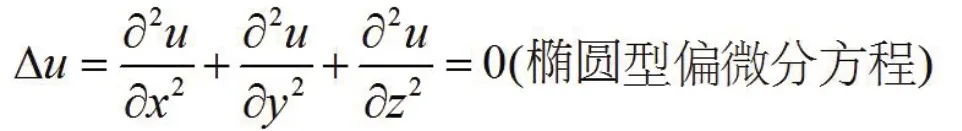
它可以用来表示溶质,稳态导热过程的动态平衡,弹性膜的平衡,也可以说是静电场电位,真空中的引力势以及不可压流体的定常运动等等。
这个方程因为抽象性而成为普适固然,方程本身的表达形式亦然很美,除符号美外,它还具对称美、简洁美),这显然也是数学本身的一大特色。
三、数学中的统一美
数学起源于哲学,哲学中的对立统一规律反映在数学上就是其统一性。统一是简单的基础,简单是数学的魅力。用统一的眼光看数学,则动与静是统一的,数与式是统一的,运算与映射是统一的,二维与三维是统一的。用统一的眼光看数学,才能将数学由厚读薄,由浅入深,才能领略到数学的简洁之美。
数学中的统一性,是指数学中部分与部分,部分与整体之间的和谐一致。数学的统一美,美在数学对客观世界和谐协调、井然有序的真实反映上。数学的统一美,使人们对数学能够居高临下、揽括一切,增强人们洞察世界的深度、广度。
微分和积分最先是当作两种数学的运算、两类的数学问题来分别以研究。但是当牛顿与莱布尼茨独立地将微分和积分真正沟通,用微积分基本定理使得这两种数学的运算统一起来,正确清楚地找到了两种运算的内在的联系:微分和积分是互逆的两种运算,微积分学才真正的建立起来。
四、数学中的对称美
“对称”这一词在古代的含意是“协调”、“雅观”。事实上,这个词是从希腊语翻译,原文的意思是“在一些物品的布置时出现的般配与和谐。毕达哥拉斯学派认为,一切空间图形中,最美的是球形;一切平面图形中,最美的是圆形。圆是中心对称图形——圆心是它的对称中心,圆也是轴对称图形——任何一条直径都是它的对称轴。毕达哥拉斯说:“一切立体图形中,最美的是球形,一切平面图形中最美的是圆形。”因为这两种形体在各个方向上都是对称的。此外,像一般的正多边形,正多面体,旋转体与圆锥曲线给出了完美的对称美。
对称是数学美的一个重要内容,它为人们提供了一个良好的平衡和充分的享受和审美,其实质是对数学概念,对立统一的重要体现,在形式和结构命题和图形中也有着不可磨灭的必要性。对称图形与其变换在几何中的是明显对称的,从最基础的圆、椭圆、双曲线到各类几何变换群的对称性都体现的非常明显,这些对称性是数学的形式美的表现,它直观给人以美的享受。但是数学中更多的是数学的基本概念、定理、法则的对称性,这也是数学内容的对称美的表现。
在小学数学中,奇数与偶数,合数与质数,约数与倍数,整数与分数,和与差等都有一种很强的对称美感。几何图形里,平行四边形的两对边等,三角形中的角与对边,都迸发着对称美的光辉。被称为最美的平面图形就是圆,这是因为圆具有最多的对称性。
总之,数学之美的每一侧面的美都不是孤立的,她们是相辅相成、密不可分的。如果在学习过程中,我们要与数学家一起探索、发现,从中获得成功的喜悦和美的享受,那么我们就会不断深入其中,欣赏和创造美。
