不同近接模式下隧道施工荷载分布规律研究

鲁 彬, 曹兴隆

(中铁开发投资有限公司, 重庆 404100)

随着我国城市化进程快速发展，城市空间利用更多的表现为地下空间的利用，地铁、地下停车场、地下交通隧道和综合管廊等的建设如火如荼。地下空间不断拓展使隧道近接施工问题越发显著。

国内外学者对于近接隧道衬砌荷载计算展开了相应的研究。Zhou Xiaojun[1]等通过大量的半圆拱直墙隧道模型研究了浅埋近接隧道宽开挖度及埋深对隧道围岩压力的影响；Wang Lichuan[2]等通过数值模拟得出了浅埋近接隧道围岩压力计算方法及破坏模式；Bai Zhe[3]等通过数值模拟得出了深河谷地形下的浅埋近接隧道的围岩压力计算理论；肖明清[4]对浅埋近接隧道围岩压力与分布进行了理论分析并提出了相应的计算方法；喻军[5]基于双坍落拱理论根据中夹岩壁下沉的大小深、浅埋近接隧的荷载模式；舒志乐[6]对偏压近接隧道围岩压力进行了探讨得出了围岩压力的理论计算公式；龚建伍[7]结合近接隧道的特点提出了浅埋隧道围压压力的分析模型和计算方法等。但目前国内外对于两近接隧道在不同位置不同净距下的荷载影响及分布模式研究较少。

本文依托某地铁区间隧道，以JTG D70-2004《公路隧道设计规范》[8]荷载设计方法为基础，运用ANSYS软件研究了不同位置及净距下的荷载影响及分布模式，为相似工程提供设计参考。

1 工程背景

本研究依托工程(采用盾构施工，盾构单洞直径5.7 m，两洞间距13 m)先开挖完成一条隧道后开挖第二条隧道。隧道下穿既有轨道交通区间隧道(采用钻爆法施工，钻爆法隧道最大水平距离9.6 m，最大竖向距离6.9 m，初衬0.27 m，二次衬砌0.45 m)，下穿段结构竖向最小净距2.57 m。

2 模型及地质参数

数值模拟采用ANSYS有限元软件，围岩采用摩尔-库伦模型，钻爆法隧道衬砌及管片均采用弹性模型。根据隧道开挖影响的一般规律，隧道开挖对围岩左右水平的影响范围为隧道直径的4～5倍，对下部围岩的影响范围为隧道直径的2～3倍，上部围岩的影响范围取到地表。综上确定模型水平长90 m，竖向长50 m，为了方便研究，选择一典型横断面地层为标准，固定钻爆法隧道为地表之间的距离，纵向取1.5 m(一环管片纵向距离)，如图1所示。既有隧道衬砌厚度450 mm，取等效直径为10 m。复合式盾构双洞隧道位于钻爆法隧道下方，直径为5.7 m，两隧道间距13 m。围岩及衬砌参数见表1。

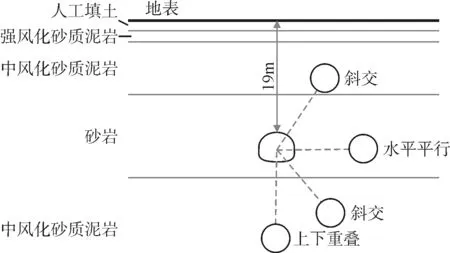
图1 典型横截面

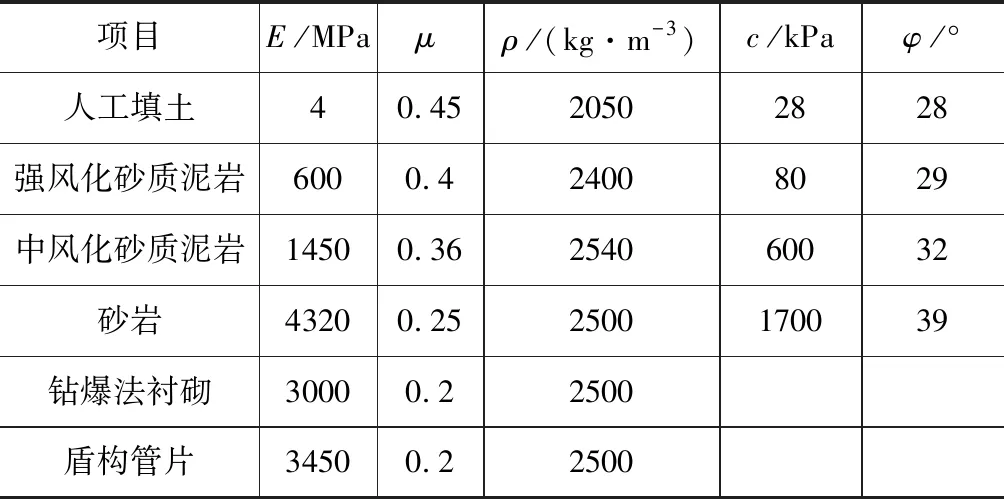
表1 围岩及衬砌参数

3 深埋近接隧道荷载影响及分布模式研究

3.1 规范法围岩压力计算方法

既有线隧道主要影响段埋深为18～30 m，围岩主要为砂质泥岩。取围岩等级为Ⅳ级，荷载高度Hq=0.45×24-1×[1+0.1×(6.6-5)]= 4.176m；主要影响段顶部以上岩层厚度大于2.5Hq，判定为深埋洞室。

JTG D70/2-2004《公路隧道设计规范》规定，计算深埋隧道衬砌时，围岩压力按松散压力考虑，其垂直及水平匀布压力：顶部围岩压力q= 91.1kPa；水平均布压力系数取0.15，e=0.15q=13.7kPa。

3.2 水平情况下荷载分布情况

通过ANSYA地层结构模型(图2)，建立管片与地层接触面分析水平平行情况下，隧道间净距分别为0.3D、0.4D和0.5D三种工况。

图2 水平平行模型

当只开挖盾构隧道时，提取接触面法向应力，隧道拱顶接触面应力如图3所示。拱顶法向应力为91.8 kPa，与隧规计算值91.1 kPa误差极小，表明了模型及接触面的合理性。

为更加清楚地分析不同工况下盾构隧道受到的围岩压力的大小和分布规律，将隧道受到的围岩荷载分为六个区域进行对比分析，如图4所示。

图3 接触应力云图

图4 围岩荷载分区

既有隧道开挖前后，各工况下接触面应力值变化如表2。

从表2可以看出：

(1)随着净距的增大，各部位荷载附加值呈减小趋势，即随着净距的增大，荷载附加值逐渐减小。

高校辅导员是与大学生直接接触最多的教师群体。辅导员日常要处理很多琐碎的事务性工作，辅导员的工作时间和地点经常不能固定，因此积极学习各种网络科技知识，能够随时随地与学生有效沟通；通过互联网进一步了解大学生积极关注的问题和现象，能够使辅导员与大学生保持在一个层面的交流，促使学生管理工作有序进行。互联网思维方式是双向互动模式，这种方式既可以优化辅导员和大学生的关系，还可以提升辅导员的工作效率。

表2 不同工况下围岩压力变化值结果 kPa

(2)水平近接影响情况下，靠近既有隧道一侧竖向荷载与水平荷载附加值明显大于远离既有隧道一侧竖向荷载与水平荷载附加值。

(3)竖向荷载区域，左半部荷载附加值远小于右半部荷载附加值。水平荷载区域上部水平荷载附加值均在一定程度上强于下部水平荷载附加值。

对于水平近接情况荷载，根据各部分荷载增加值情况，可将上部与左部荷载增加值等效为一个三角附加荷载，将右部分水平荷载等效为一个均布附加荷载，见图5。

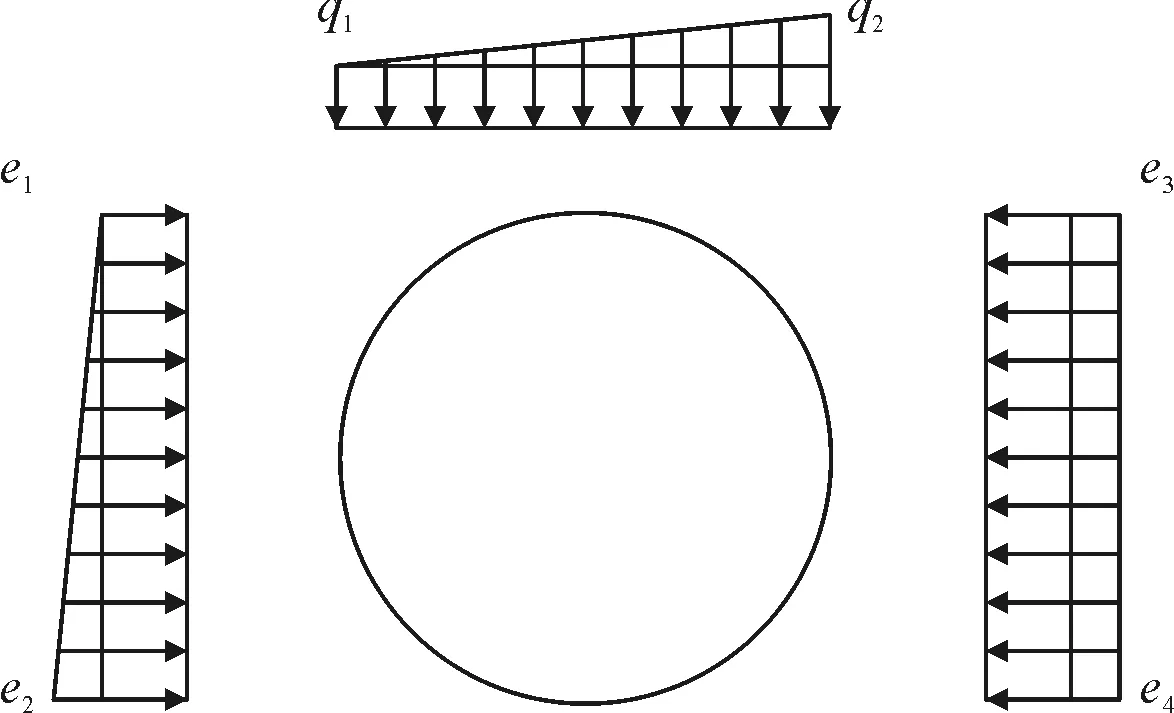
图5 水平情况下荷载分布示意

将总荷载按上述分布模式分别分布到各部位可得表3(式中e、q为规范计算下荷载取值，下同)。

表3 各部分隧道设计值

3.3 斜交45 °情况下荷载分布情况

通过ANSYA地层结构模型，通过建立管片与地层接触面分析斜交45 °情况下，隧道间净距分别为0.3D、0.4D和0.5D三种工况。如图6所示。

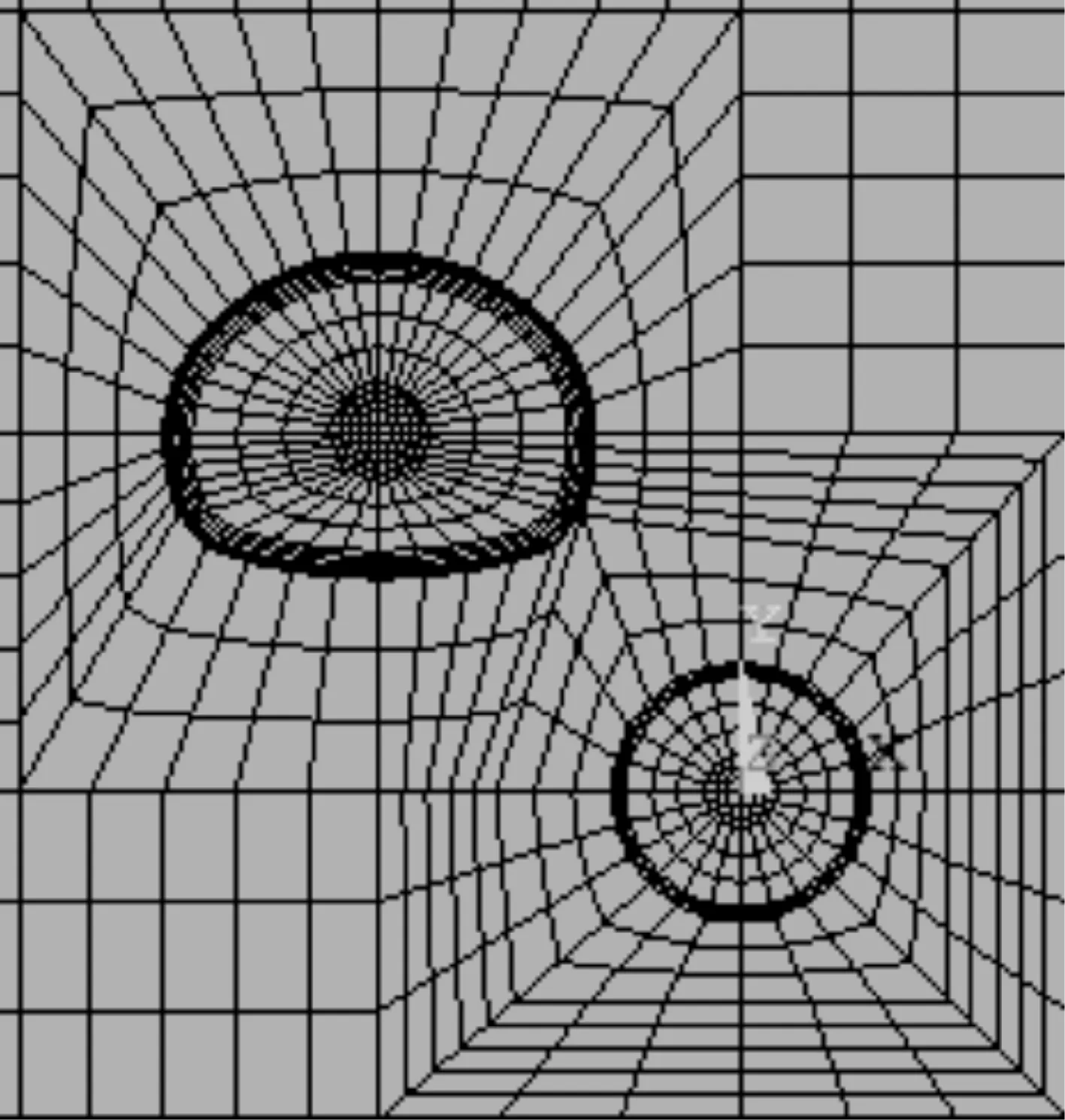
图6 斜交45°模型

当只开挖盾构隧道时，提取接触面法向应力，其拱顶法向应力为90.8 kPa，与隧规计算值91.1 kPa误差极小，表明了模型及接触面的合理性。

同上节相似，既有隧道开挖前后，各工况下各部分接触面应力值变化如表4所示。

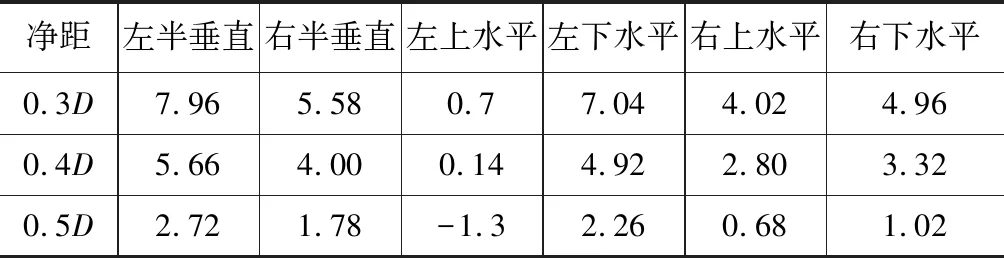
表4 不同工况下围岩压力变化值结果 kPa

从表4可以看出：

(2)受既有隧道开挖影响，靠近既有隧道一侧水平荷载附加值明显小于远离既有隧道一侧水平荷载附加值。靠近既有隧道一侧拱顶竖向荷载附加值大于远离既有隧道一侧竖向荷载附加值。

(3)竖向荷载区域，左半部荷载增量大于右半部荷载增量。左部水平荷载区域上部水平荷载增量远小于下部水平荷载增量，右部水平荷载区域上部附加值小于下部水平荷载附加值。

对于斜交45 °情况荷载，根据各部分荷载增加值情况，可将上部与左部荷载增加值等效为一个三角附加荷载，将右部分水平荷载等效为一个均布附加荷载，见图7。

图7 斜交情况下荷载分布示意

将总荷载按上述分布模式分别分布到各部位如表5所示。

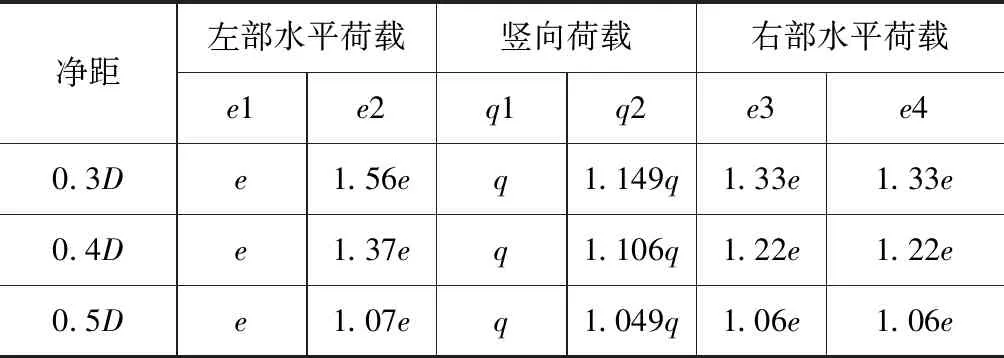
表5 不同工况下围岩压力变化值结果 kPa

3.4 上下重叠情况

通过ANSYA地层结构模型，通过建立管片与地层接触面分析上下重叠，隧道间净距分别为0.3D、0.4D和0.5D三种工况。如图8所示。

图8 斜交45°模型

当只开挖盾构隧道时，提取接触面法向应力，其中拱顶法向应力为91.3 kPa，与隧规计算值91.1 kPa误差极小，表明了模型及接触面的合理性。既有隧道开挖前后，各工况下各部分接触面应力值变化如表6所示。

表6 不同工况下围岩压力变化值结果 kPa

从表6可以看出：

(1)由于上部既有隧道开挖，各部分附加荷载都为负值，随着净距的增大，附加荷载的大小逐渐降低。

(2)由于既有隧道位于正上方，竖向附加荷载与水平附加荷载呈对称分布。且下部水平附加荷载大于上部水平附加荷载。

(3)竖向荷载附加值明显大于水平荷载的附加值，表明拱顶受开挖影响更大。

对于上下重叠情况荷载，根据各部分荷载增加值情况，可将左部与右部水平荷载附加值等效为一个三角附加荷载，将竖直附加荷载等效为一个均布附加荷载，见图9。

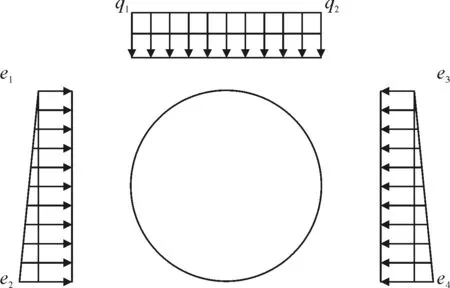
图9 斜交情况下荷载分布示意

由于所有附加荷载都为负值，保守起见，可采用规范荷载作为隧道设计荷载。

4 应用实例

依托工程区间隧道左右线与既有线隧道净距及位置不断变化，按照近接分区结果将近接隧道沿线路纵向进行分段，相应的设计按表7所示。

表7 近接影响区段

5 结论

本文基于依托工程地质与埋深情况，通过数值模拟分析了不同净距及位置下的荷载附加值，并基于荷载变化情况给出了相应的荷载分布模式。

(1)水平平行及斜交45°情况下，随着净距的增大，各部位荷载附加值呈减小趋势，即随着净距的增大，荷载附加值逐渐减小。受既有隧道开挖影响，靠近既有隧道一侧水平荷载附加值明显小于远离既有隧道一侧水平荷载附加值。靠近既有隧道一侧拱顶竖向荷载附加值大于远离既有隧道一侧竖向荷载附加值。

(2)上下垂直情况下，由于上部既有隧道开挖，各部分附加荷载都为负值，随着净距的增大，附加荷载的大小逐渐降低。竖向附加荷载与水平附加荷载呈对称分布，且下部水平附加荷载大于上部水平附加荷载。