刚度连续、单调且光滑变化的粗糙界面法向弹塑性接触模型

肖会芳，孙韵韵，徐金梧

(1.北京科技大学 机械工程学院，北京，100083；2.北京科技大学 钢铁共性技术协同创新中心，北京，100083)

粗糙接触界面广泛存在于机械结构与机器设备中，例如齿轮的轮齿啮合界面、轴承的滚动体-滚道界面、机床螺栓联接界面、高速列车的车轮-轨道形成的轮轨界面等[1-4]。粗糙界面接触刚度是机械结构整体刚度的重要组成部分，也是描述界面特性最重要的参数之一，其变化直接影响界面以及机械装备系统的静态特性和动力学特性，包括接触压力分布、振动响应特性、磨损特性以及工作稳定性等[5-7]。因此，粗糙界面法向接触刚度的准确计算对机械结构与系统的性能分析与预测至关重要。在微观尺度下，粗糙表面可以看成是具有一定曲率半径的单个微凸体按照不同的分布特征形成的整体。随着外部载荷增加，微凸体的变形量增大，单个微凸体的变形状态经历弹性变形、弹塑性变形和完全塑性变形。其中，弹性变形阶段的接触特征通常采用Hertizan 接触模型表征[8]；完全塑性变形阶段的接触特征通常采用线性硬度模型表征[9]。而处于中间过渡区的弹塑性变形阶段接触模型，需要保证微凸体的接触状态变量，包括接触压力、接触载荷和接触刚度等，从弹性阶段单调、连续且光滑过渡到完全塑性阶段。为了满足不同接触状态之间单调、连续且光滑的条件，研究人员提出了不同的弹塑性模型来表征界面的法向接触特性。ZHAO等[10]基于CHANG等[11]的弹-塑性模型，利用插值方法建立了弹塑性变形状态下实际接触面积、平均接触压力与法向接近量之间的关系，提出了一种粗糙界面的弹塑性接触模型(ZMC 模型)。但是，平均接触压力和接触载荷的变化在临界点处不光滑，导致接触刚度在临界点处不连续，且刚度变化不是单调的。赵永武等[12]进一步对ZMC 模型进行改进，基于三次样板函数插值的方法，提出了一种在临界点满足连续性和光滑性要求的法向接触模型(MZMC 模型)。虽然接触刚度随法向变形量的变化关系是连续的，但是不光滑和非单调。BRAKE[13]采用Hermit 多项式插值的方法，提出了一种满足不同接触状态之间光滑和连续过渡的粗糙表面弹塑性接触模型。但是，由于Hermit 多项式的阶次较高，插值获得的弹塑性阶段平均接触压力与法向变形量之间的关系曲线出现振荡，使得接触压力和接触刚度的变化过程并非单调。徐超等[14]提出一种利用低阶椭圆曲线插值进行解析建模的方法，建立了粗糙界面弹塑性阶段接触模型，该模型能够描述微凸体的接触压力和接触面积随法向接近量单调、连续和光滑的变化过程，但是，界面的法向接触刚度仍然具有非单调的缺点。针对上述弹塑性接触模型的不足，本文作者提出一种新的粗糙界面法向接触弹塑性模型，该模型能够描述微凸体的接触状态变量，包括接触载荷、接触面积和接触刚度，在不同接触状态之间连续、光滑且单调变化。在此基础上，基于粗糙界面微凸体高度分布概率密度函数，推导获得整个粗糙界面的法向接触刚度表达式。

1 单个微凸体接触刚度模型

单个微凸体与刚性平面的接触示意图如图1所示。表面粗糙体的形状为球体且各粗糙体的曲率半径均为β，单个微凸体的高度z定义为微凸体顶点与微凸体高度均线间的距离。微凸体均线与粗糙面均线之间的距离为dd，dd=1.15σs[15]，σs为粗糙微凸体高度分布的标准偏差。

图1 单个微凸体与刚性平面接触示意图Fig.1 Geometry of single asperity contact

1.1 弹性接触(w＜w1)

根据Hertzian 弹性接触理论，其弹性接触力可以表示为[8]

式中：E为接触界面的等效弹性模量；w为弹性变形量，可以表示为

由式(5)可知，弹性变形阶段，单个微凸体的法向接触刚度与变形量呈非线性变化关系。微凸体从弹性变形过渡到弹塑性变形的临界变形量w1[16]为

式中：H为材料硬度；K为硬度系数，与材料的泊松比相关，K=0.454+0.41v。

1.2 完全塑性接触(w＞w2)

当微凸体的法向变形量w＞w2时，微凸体发生完全塑性变形，其临界变形量w2[17]为

此时，界面的平均接触压力pp为材料的硬度H，即

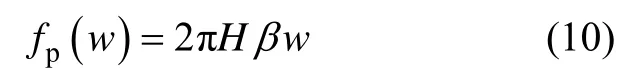
微凸体的法向接触刚度kp可以表示为

由式(11)可知，完全塑性变形阶段，单个微凸体的法向接触刚度为常数，与变形量无关。

1.3 弹塑性接触(w1＜w＜w2)

当微凸体的变形量w1＜w＜w2时，界面处于弹塑性变形阶段。随着微凸体变形量增大，微凸体从弹性变形过渡到弹塑性变形，直至完全塑性变形阶段的整个过程，接触状态参量应该满足连续、光滑且单调的条件。为了满足不同接触状态之间单调、连续且光滑的条件，研究人员提出了不同的弹塑性模型，以表征界面的法向接触特性。

1.3.1 ZMC 模型

根据ZMC 弹塑性接触模型，弹塑性变形阶段的平均接触压力为[10]

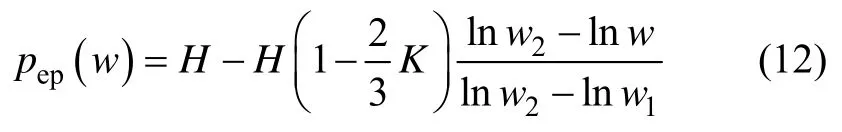
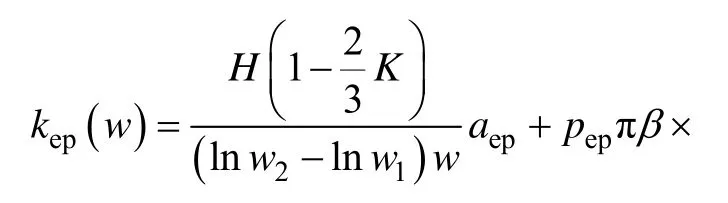
1.3.2 改进的ZMC 模型(MZMC 模型)

其中：

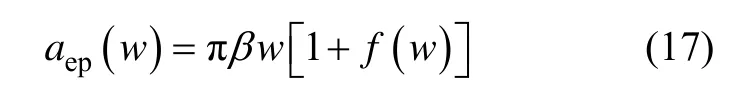
1.3.3 Brake 模型

其中：

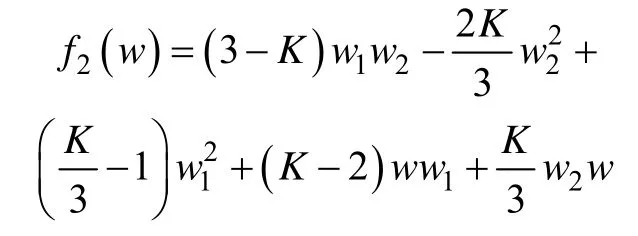
则接触刚度kep(w)可以表示为

1.3.4 Xu 模型

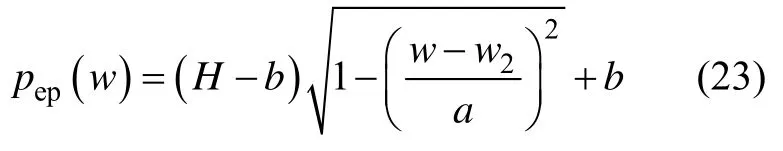
其中：

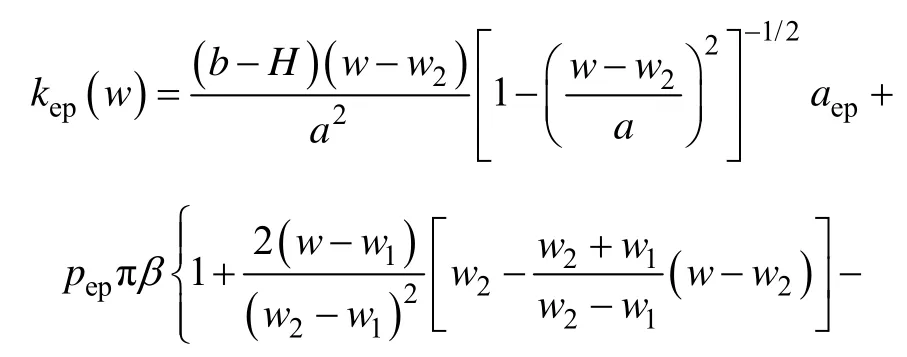
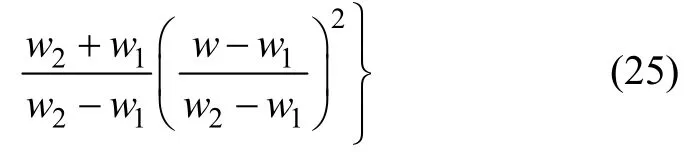
1.3.5 本文模型

为了满足单个微凸体接触刚度在弹性、弹塑性和完全塑性的不同接触之间变化的连续、光滑和单调性要求，本文提出采用低阶椭圆曲线来表征微凸体弹塑性阶段接触刚度，并通过对刚度表达式积分，获得微凸体弹塑性阶段载荷关系式的弹塑性接触模型。

单个微凸体接触刚度的表达式为

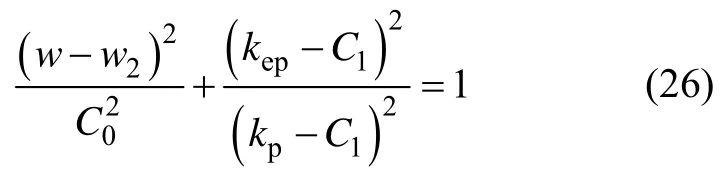
其中：C0和(kp-C1)分别为椭圆函数的长半轴和短半轴，kp=2πβH，C0和C1为待定系数，由弹性变形到弹塑性变形临界变形量w1处刚度的连续性和光滑性条件确定。

对式(26)求导，可得

将连续性和光滑性边界条件式(27)代入式(26)和(28)，则有

单个微凸体的接触刚度可以表示为

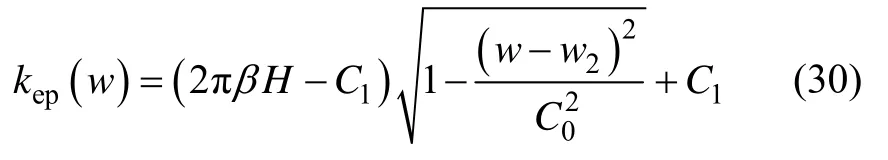
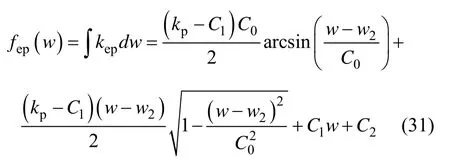
其中：C2为待定系数，由弹性变形到弹塑性变形临界变形量w1处载荷的连续性条件确定，即

将式(32)代入式(31)，有

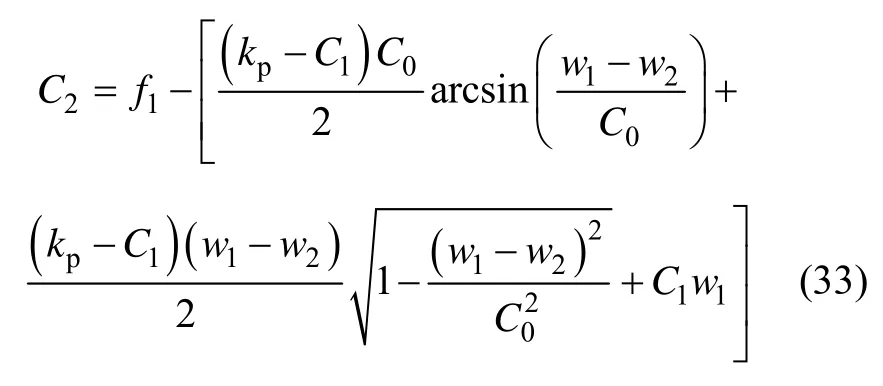
单个微凸体的接触面积表达式采用三次样板函数描述，表达式为

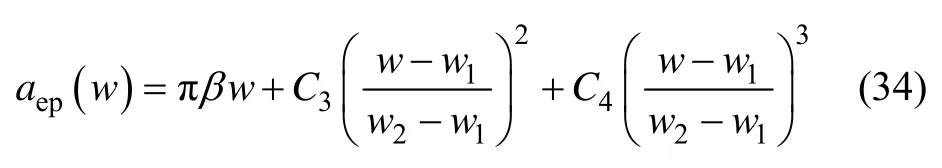
其中：C3和C4为待定系数，由临界变形量w1和w2处面积的连续性条件确定，

将式(35)代入式(34)，有

1.4 不同模型计算结果分析

采用不同弹塑性模型计算获得的单个微凸体的接触面积、接触载荷和接触刚度随法向变形量的变化关系曲线，分别如图2～4所示，计算参数为E=52 GPa，v=0.25，H=6.2 GPa，β=0.182 mm。由图2可知：对5种不同的弹塑性接触模型，在整个弹性、弹塑性和完全塑性变形状态，接触面积随法向变形量的变化关系曲线均为单调、连续且光滑的。

图2 不同模型计算获得的单个微凸体接触面积Fig.2 Contact area of single asperity contact for different models

接触载荷的变化关系曲线却并非均为单调、连续且光滑，如图3所示。对ZMC 模型，接触载荷随法向变形量的变化曲线单调且连续，但是在临界变形量w2处不光滑，由此导致接触刚度在临界变形量w2处不连续，如图4所示。对MZMC 模型和Brake 模型，由于接触载荷表达式多项式的阶次较高，使得接触载荷随法向变形量的变化曲线非单调，导致接触刚度随法向变形量的变化出现震荡，甚至出现负刚度。对Xu模型，接触载荷随法向变形量的变化曲线单调、连续且光滑，但是其接触刚度随法向变形量的变化曲线却非单调。对本文提出的模型，接触载荷和接触刚度随法向变形量的变化曲线均为单调、连续且光滑变化。

图3 不同模型计算获得的单个微凸体接触载荷对比Fig.3 Contact force of single asperity contact for different models

图4 不同模型计算获得的单个微凸体接触刚度Fig.4 Contact stiffness of single asperity contact

2 粗糙界面接触刚度模型

采用GW 统计学模型计算粗糙界面上接触微凸体数[18]，并将单个微凸体接触刚度和载荷对微凸体数进行积分，获得粗糙界面接触的总刚度和总载荷。粗糙界面接触模型示意图如图5所示。

图5 粗糙表面与刚性平面的统计接触模型Fig.5 Statistical micro-contact model of rough surface

引入如下量纲一的量：

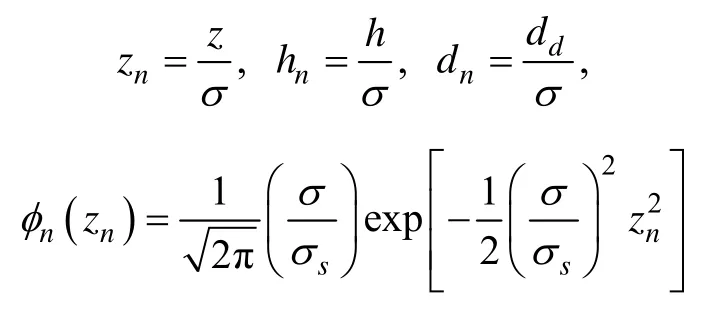
当微凸体高度zn 大于粗糙面均线与刚性平面之间的距离hn-dn时，微凸体与刚性平面接触，其接触概率为[18]

式中：N为粗糙表面微凸体总数，N=nAn；n为微凸体分布密度；An为名义接触面积。

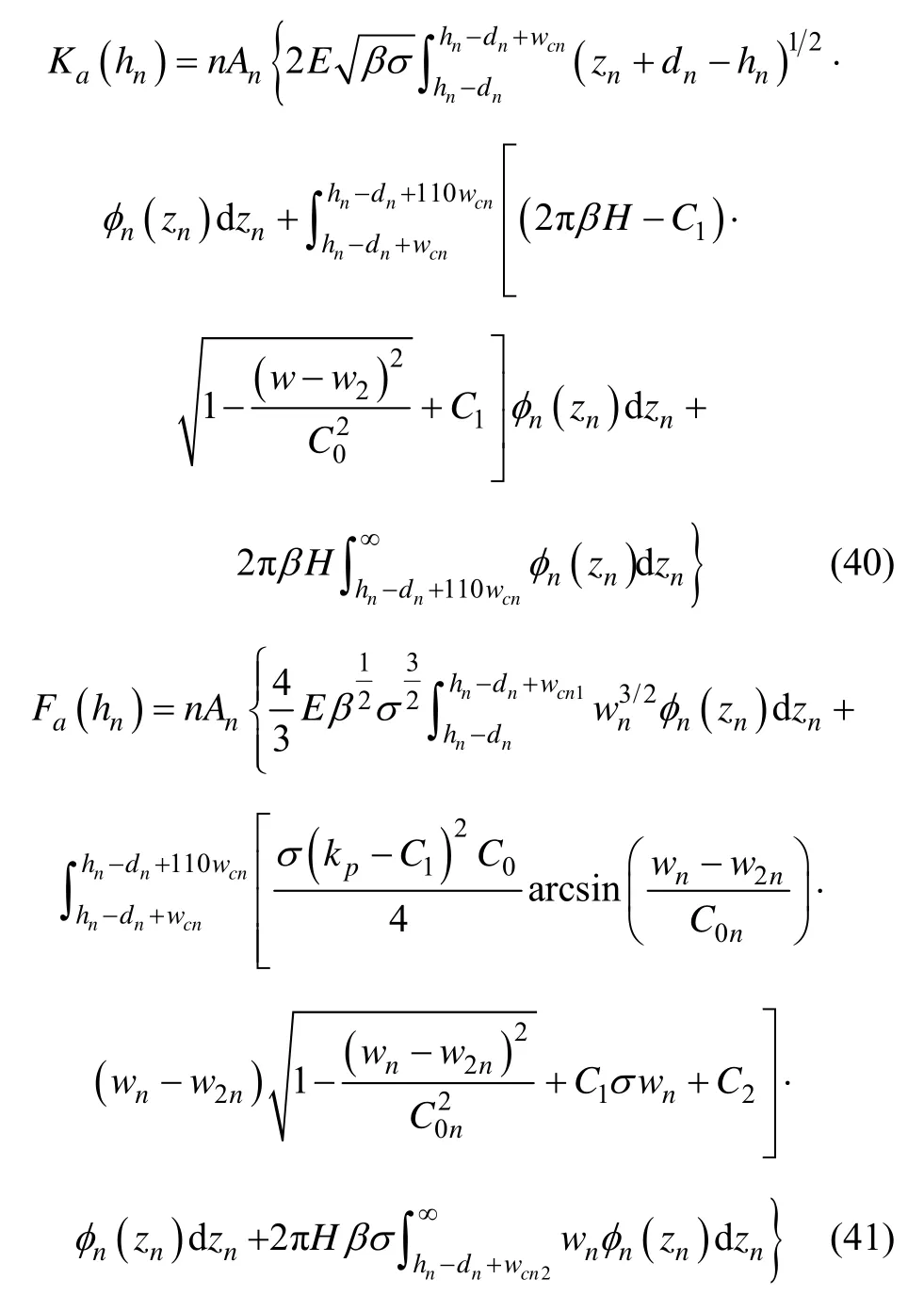
将不同变形阶段单个微凸体的刚度表达式和载荷表达式分别代入式(38)和(39)，则粗糙界面的接触刚度和载荷可以分别表示为

3 粗糙界面接触刚度模型验证与结果分析

3.1 模型验证

文献[19]采用超声反射系数法测量了不同接触面积钛合金Ti-6Al-4V 粗糙界面的接触刚度，钛合金的材料参数为E=115 GPa,v=0.31，界面的微凸体高度标准偏差σs=2.3 μm。采用本文接触刚度模型式(40)和式(41)计算获得的法向固体接触刚度-载荷变化关系曲线与文献[19]实验测量获得的结果对比图，如图6所示。由图6可知，模型的计算结果与实验测试结果基本一致，说明本文的界面固体接触刚度的模型是有效的、可靠的。

图6 粗糙界面固体接触刚度的模型计算结果与实验结果[19]对比Fig.6 Comparison of solid contact stiffness versus pressure between model results and experimental results[19]for different nominal area

3.2 不同粗糙度界面刚度

光滑界面、中等粗糙界面和粗糙界面的表面形貌参数[20]如表1所示。对不同粗糙度界面，采用本文提出的弹性-弹塑性-完全塑性刚度模型式(40)和式(41)计算获得的界面接触总刚度随接触载荷的变化关系曲线如图7所示，并与纯弹性接触GW 模型计算获得的刚度-载荷关系曲线进行对比。

表1 不同粗糙度表面形貌参数Table 1 Parameters of surfaces with different roughness

图7 不同粗糙度界面的法向接触刚度随载荷的变化关系曲线Fig.7 Variation of normal contact stiffness with normal load for different roughness

由图7可知：考虑弹性-弹塑性-完全塑性不同接触状态刚度模型计算获得的刚度大于纯弹性GW 接触模型的刚度计算值，且随着表面粗糙度增大，2 种不同模型获得的刚度差值逐渐增大。这是由于随着表面粗糙度增大，界面从弹性变形过渡到弹塑性变形的临界变形量w1逐渐减小，弹塑性变形阶段对界面接触状态的影响逐渐增大，导致2 种模型获得的刚度差值逐渐增大。

由图7还可知：粗糙界面接触刚度随法向载荷呈非线性递增，且增大的幅度随载荷的增大逐渐减小(曲线的斜率逐渐减小)；随着表面粗糙度增大，法向接触刚度逐渐减小。

4 结论

1)提出一种新的基于低阶椭圆曲线的微凸体法向弹塑性接触刚度模型，该模型考虑粗糙界面的弹性变形、弹塑性变形和完全塑性变形接触状态，且保证不同接触状态之间微凸体的接触刚度、接触载荷和接触面积均连续、单调且光滑变化，克服了以往模型的接触刚度非连续、非单调的缺点。

2)基于微凸体高度分布概率密度函数，推导获得了整个粗糙界面接触刚度和接触载荷表达式，建立了整个粗糙界面接触刚度模型。

3)模型计算结果与实验测量结果基本一致，验证了本文建立的粗糙界面接触刚度模型的有效性。

4)考虑弹性-弹塑性-完全塑性不同接触状态刚度模型计算获得的刚度大于纯弹性接触GW 模型刚度计算值，且随着表面粗糙度增大，2 种模型获得的刚度差值递增。

5)粗糙界面接触刚度随法向载荷呈非线性递增，随着表面粗糙度的增大而减小。