数控电路板性能退化分析及可靠性统计推断研究
2019-07-19解传宁
解传宁
(烟台大学机电汽车工程学院,山东 烟台 264005)
印刷电路板作为一种重要的基础元件,在数控、航天、航空等领域中应用广泛.随着现代科学技术的发展要求,印制电路板的性能和可靠性水平成为影响电子装备完成既定任务的重要因素之一[1].由于印制电路板属于高可靠性、长寿命产品,即使采用加速寿命试验,也会出现极少失效甚至零失效的现象,这给其在给定时间内的可靠性评定带来了困难.由于大部分产品的失效机理或者说故障原因可以追溯到其性能退化过程,因此在某种意义上说产品失效或者说故障的发生可以认为是其性能退化引起的,因此通过研究产品的性能变化规律进行可靠性评估是可靠性研究的一个新方向[2-3].产品的性能退化过程包含大量的可靠性信息,因此,基于产品的性能退化过程进行可靠性分析,是一种解决高可靠性、长寿命产品可靠性评估问题的良好方法[4-5].本文以数控用印制电路板进行性能退化试验,通过收集和分析该数控电路板的性能退化数据,对数控电路板的可靠性进行了探讨.
1 性能退化试验
1.1 性能退化基本概念
性能退化是指在产品内部机理与外界环境的综合作用下,产品性能随时间变化的一种复杂的物理/化学过程,这一性能变化随着时间的累积发展并达到一定量级时就会发生损伤,当这种损伤量达到一定阈值(通常称为失效标准或失效阀值)时,产品就会发生失效,通过产品性能退化量来估计产品可靠性的试验,称为退化试验[3-7].目前,应用性能退化试验进行可靠性统计推断成为解决高可靠性、长寿命产品可靠性评估问题的重要手段之一[7-8].
为保证性能退化试验能正常进行,需要保证试验在下面3个基本假定前提下进行的[8]:
假定1 在各应力水平下,产品失效机理均保持不变;
假定2 在各应力水平下,产品的性能退化过程呈现出一定的规律性;
假定3 在各应力水平下,产品的退化过程服从同族随机过程,即应力水平变化时,产品退化随机过程保持不变,改变的只是过程参数.
1.2 产品性能退化特征参数
在性能退化试验的研究中,确定性能退化特征参数是退化试验开展的前提.性能退化特性参数必须具备2个条件[4,7,9]:一是能准确定义而且能够进行监测;二是随着试验时间的延长,有明显的趋势性变化,能客观反映产品的工作状态.在产品的性能退化特征参数采集过程中,进行连续数据采集是比较困难的,因此在试验过程中,可以规定一定时间间隔来测量产品的性能退化特征参数值并进行记录.相对于完全失效寿命数据来说,记录下来的性能退化数据包含了更多的关于产品性能劣化信息,减少了失效时间数据丢失的信息,可以得到更准确的可靠性推论.
2 数控电路板退化试验及统计分析
2.1 数控电路板性能退化原因
由于绝缘性能下降引起的漏电或短路故障是印制电路板使用过程中最常见的失效形式,如电路板本身绝缘性不足,污染物残留导致腐蚀,电化学迁移引起绝缘性能下降等[10-11].其中,电极之间的电化学迁移是导致电路板绝缘性能劣化甚至造成短路的主要原因[12].《IPC-9201 表面绝缘电阻手册》中定义,“当印制电路板或其组装件长期处于高温高湿的恶劣环境中,其相邻导体间又有偏压的情况下,逐渐发生的金属离子迁移,并在板面析出金属或其氧化物,该过程称为电化学迁移,析出物质一般呈树枝状而被称为枝晶”[10-13].枝晶生长是金属在电场作用下,发生的金属离子溶解、迁移和沉淀过程.在不同电场作用下的枝晶SEM形貌显示,枝晶生长速率是随着加载电场强度增大而增大的,高电场强度下,枝晶生长速率较快,低电场下生长速率较慢[14-15].另外,印制电路板所使用的基材包括酚醛纸基覆铜板、环氧玻璃布(FR-4)覆铜板等多种,其中用FR-4覆铜板加工的印制电路板,由于其具有强度高、耐热性好、介电性能好、性价比高等特点,从而在数控系统中被广泛应用,但是,FR-4覆铜板的吸水性偏高,且电路板所使用的半固化片(黏接片)对湿度是十分敏感的[16-17],因此数控电路板电化学迁移的发生率比较高,这对数控系统的绝缘可靠性提出了挑战.
同时,随着数控系统功能越来越强大,集成电路封装技术不断向着高度集成化、高性能化、多引线和细间距化等方向发展,使得数控电路板层数不断增加,导线宽度和线距都趋于微细化,而数控装备工作地域越来越广泛,气候环境越来越恶劣,因此,数控电路板发生电化学迁移的概率进一步提高.数控电路板在工作过程中发生电化学迁移的危害主要体现在,湿度较大地区的空气水分为金属离子溶解和沉淀提供了溶液媒介,数控装备在高速负载操作下运行,电路板温度不断上升,加深了化学反应程度,同时这种湿热的环境为离子迁移提供了通道,此外,电路板上的导电电路本身处于带电状态,为电化学迁移的形成提供了电势差,为离子迁移和枝晶生长获得了动力,枝晶的形成最终导致电路板绝缘性能降低,严重时引起线路间的短路,以至于烧毁元器件[17].
2.2 数控电路板性能退化特性分析
根据2.1节电化学迁移形成过程的分析,可知偏置电压是其离子迁移和枝晶形成的驱动力.为研究偏置电压对数控电路板绝缘性能的影响,本文开展电压应力性能退化试验.试验以数控电路板为测试样板,电压应力选取4水平:12 V,24 V,220 V和380 V.
根据试验需求,试验选用广州艾斯佩克高低温湿热环境试验箱开展试验和测试工作,试验现场如图1.通过查阅国内外相关印制电路板的性能规范与测试方法可以看出,印制电路板绝缘性能的评价基本是通过绝缘电阻来表征[10,13,17],绝缘电阻可以满足1.2节提出的性能退化特性参数具备的条件,故本文选取绝缘电阻为退化特征参数.试验通过监测数控电路板在4应力水平下的绝缘电阻值变化来研究偏置电压对数控电路板绝缘性能的影响.
由定义可知,电化学迁移是在高温高湿和施加偏置电压的条件下发生的,为保证电化学迁移的发生,试验中设置环境温度和湿度分别为85℃,85%RH.当试验箱内环境条件达到设置值并稳定运行后再对试验样板施加不同水平的偏置电压,在设定时间间隔用绝缘电阻测试仪分别测试各样板的绝缘电阻,整理不同偏置电压水平下的测试样板的绝缘电阻值(IR)随时间t的试验数据,如图2.由图2可见,在同一电压应力水平下绝缘电阻值(IR)随时间t以一定趋势变化,变化趋势明显,进而确定偏置电压是影响绝缘失效的主要应力,同时可以看出,绝缘电阻(IR)在不同偏置电压水平下随时间t变化轨迹不尽相同.

图2 绝缘退化数据轨迹
同时,由图2可见,数控电路板绝缘电阻值在施加偏置电压后的一段时间内,出现绝缘电阻值的急剧下降,经过一段时间的处理,急剧下降的绝缘电阻值又开始慢慢恢复,之后绝缘电阻值随时间呈现有规律的下降.这是由于电化学迁移现象是一种复杂的物理化学过程,试验中绝缘电阻值急速下降的情况,可能是在高温高湿的环境下由附有了水滴所引起的离子迁移造成电路板表面枝晶的扩展,从而形成一种电极间的电桥接造成导电通路,但随着枝晶的间隙部分逐渐扩大,又使得绝缘电阻值得以恢复,此阶段未发生析出物,当继续施加偏置电压后,离子迁移发生,绝缘电阻随时间的延长而发生不断的下降,此时离子沿着基材内层纤维移动,并伴随析出物[18].因此,结合图2可以推断,电路板在施加偏置电压150 h后,电化学迁移失效发生,绝缘电阻值随着试验时间的延长,呈现稳定的绝缘性能退化趋势,可以客观反映电路板的工作状态.因此,整理数控电路板150 h后的绝缘电阻值与时间的退化数据如表1所示.

表1 试验性能退化数据记录表
2.3 试验数据统计分析
基于表1的退化数据,本文对各偏置电压应力水平下的测试样板进行退化轨迹模型拟合,用以预测印制电路板的可靠性.为了计算方便,同时为了初步对退化曲线轨迹模型进行直观地分析,不妨对表1中绝缘电阻值取对数,得到绝缘电阻值对数化的值随时间的轨迹,如图3.由图3可以看出,测试样板绝缘电阻对数化后的轨迹基本呈线性,因此可以初步选择如下退化轨迹模型:
lnyt=αi+βit,
(1)
式中:t为试验时间;yi为退化特征参数量,即绝缘电阻;αi、βi为待计算参数.
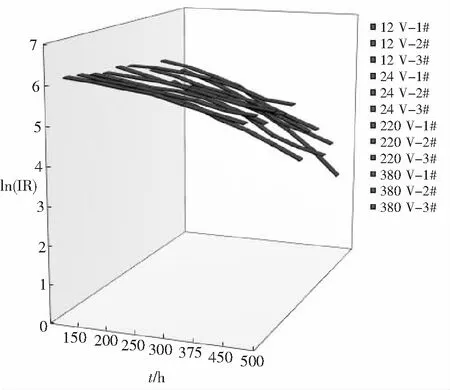
图3 对数化的轨迹曲线
由于最小二乘法计算精度高,统计性质良好,因此工程计算中经常选用最小二乘法进行曲线拟合.本试验基于表1中的性能退化数据,利用最小二乘法对各样板的退化轨迹模型的未知参数进行估计,得到各样板退化轨迹模型的参数值,其结果如表2所示.
表2 各样本退化轨迹模型参数估计值与伪失效寿命
Tab.2 The parameter values of each degradation model and pseudo-failure lifetime
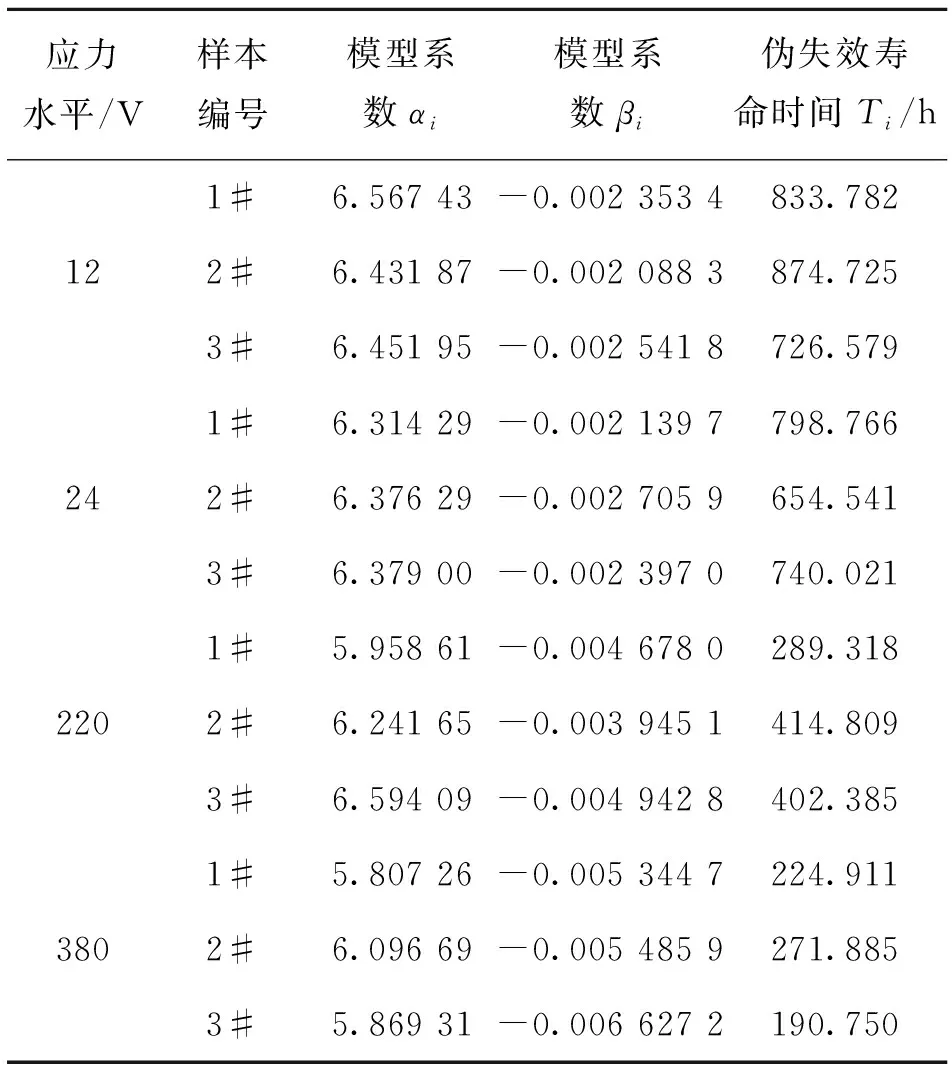
应力水平/V样本编号模型系数αi模型系数βi伪失效寿命时间Ti/h1#6.567 43-0.002 353 4833.782 122#6.431 87-0.002 088 3874.7253#6.451 95-0.002 541 8726.579 1#6.314 29-0.002 139 7798.766 242#6.376 29-0.002 705 9654.5413#6.379 00-0.002 397 0740.021 1#5.958 61-0.004 678 0289.318 2202#6.241 65-0.003 945 1414.8093#6.594 09-0.004 942 8402.385 1#5.807 26-0.005 344 7224.911 3802#6.096 69-0.005 485 9271.8853#5.869 31-0.006 627 2190.750
YANG S 等[19]在研究电化学迁移的失效机理过程中,指出当绝缘电阻IR降到100 MΩ时,便可认定电路板绝缘失效,这也与标准IPC-TR-476 A[20]和IPC J-STD-004[21]相符.据此,结合数控系统工作任务,本文规定试验样板失效阀值为100 MΩ.因此,根据表2得到的不同应力水平下样板的退化轨迹模型,代入失效阈值100 MΩ,外推求出每个样板达到失效阈值的失效时间.这些时间并不是产品的实际失效时间,因此称其为伪失效寿命时间(Pseudo-failure lifetime),其结果如表2最右侧一列所示.
3 数控电路板可靠性评估
3.1 退化失效模型的确定
由于试验的样本量较小,很难对失效数据进行寿命分布检验.根据文献[15,22]中的研究发现电路板的失效寿命近似服从威布尔分布.其分布函数为
F(t)=1-exp[-(t/ηi)mi],i=0,1,…,k,
(2)
式中:ηi,mi分别为产品在应力水平Si下的特征寿命和形状参数.
根据数控电路板的失效机理分析可以得到,随着施加偏置电压的提高,电化学迁移析出物生长更快.在物理学上已经总结出逆幂律关系函数来反映产品寿命与电压的关系.因此这里可以认为数控电路板的寿命t与偏置电压V之间的关系符合逆幂律模型,其模型如下:
t=1/(dVc)=AV-c,
(3)
式中:t表示产品寿命;A、d、c为待定常数;V表示偏置电压.
当产品退化失效机理不变时,形状参数mi为与时间和应力无关的常量,特征寿命ηi为与应力有关的时变参量.当加速应力为偏置电压时,退化失效方程为
lnηi=a+bφ(Si)=a+b·lnVi,
(4)
式中:a,b为待估参数,且a=lnA,b=-c.
3.2 退化失效模型参数估计
利用加权最小二乘法和Gauss-Markov定理,可得到退化失效模型(4)的参数a,b的估计,即

(5)

(6)

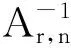
为了计算式(5)和(6)中系数H和M值,先要计算特征寿命lnηi和形状参数mi估计值.对于小样本的情况下,一般希望估计量的均方差最小,最好线性无偏估计(BLUE)等方法得到的无偏估计量的均方差不一定是最小的,而最好线性不变估计(BLIE)得到的估计量的均方差小于其他估计的均方差[24].因此将伪失效寿命数据视为完全寿命数据,对不同应力水平下的威布尔分布参数,mi采用最好BLIE方法进行求解,其计算公式如下:
(7)
(8)
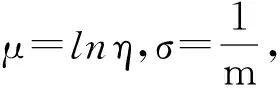

表3 各应力水平下各参数计算结果
同时根据《可靠性试验用表》[23]计算电路板寿命分布总体参数m的估计为
(9)
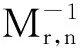

(10)
据此,威布尔分布的平均寿命,即电路板的失效寿命可以近似计算为
亦即
E(T)=2 099.176·V-0.334 34Γ(1.084 12),
(11)
式中:Γ(·)为伽马函数
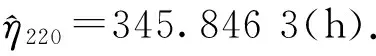
E(T)=345.846 3×Γ(1.084 12)=
345.846 3×9 579.52=3 313 041.55(h).
已有研究表明[19],在电化学迁移过程中,当电路板在高于65 ℃工作时,环境湿度对电路板电化学迁移的影响微乎其微,因此可以忽略湿度对电路板寿命的影响.据此可以根据Egring模型进行不同温度θ下的电路板的寿命换算,换算公式可以化简为
(12)
式中:tθ为在温度θ下的平均寿命.
根据公式(12),数控电路板在25 ℃下的平均寿命可以近似计算为
t25=exp(1.2·ln 3 313 041.55)=66 722 492.12(h).
其他可靠性指标的估计可以类似得到.
4 结 语
基于性能退化数据的统计分析方法研究,本文以数控用印制电路板为试验对象,通过分析其失效机理,研究其性能退化规律,建立了退化失效模型;通过在高温高湿环境下对数控电路板进行偏置电压退化试验,观测到电路板在不同偏置电压应力水平下的绝缘电阻随时间变化的退化过程,建立了绝缘电阻随时间变化的退化轨迹模型,利用最小二乘法对退化轨迹进行参数估计;结合失效阀值对退化轨迹外推得到各应力水平下的伪失效寿命,最后将伪失效寿命看作完全寿命数据,根据完全寿命数据的统计分析方法进行统计分析.结果表明,基于性能退化数据进行数控电路板可靠性评估,可以在更短的时间内较准确地完成寿命预测,节省试验时间,具有在无失效数据和极少失效数据的情况下仍能适用的优势,为由板级升级到数控系统级的可靠性评估奠定了基础.
