内置加劲环T型管节点抗冲击承载力分析

高 康,曲 慧,丛静岚

(烟台大学土木工程学院,山东 烟台 264005)

钢管结构凭借其轻质高强、材质均匀、塑性韧性好等优点在各类建筑工程中得到了广泛的应用,例如飞机场,火车站,海洋钻井平台等．当其遭受到外来物体撞击时,会因管节点失效引起传力路径发生改变,因此研究加强后管节点的抗冲击性能是目前研究的热点．在冲击荷载作用下,T型管节点的抗冲击承载力是评价管结构抗冲击性能的一个重要指标．陈栋芬[1]对T型钢管进行了极限承载力分析,根据试验数据修正了极限承载力计算公式．ELLINAS等[2]将钢管两端固支进行跨中冲击试验,根据试验数据推出局部凹陷和整体弯曲的经验公式．YOUSUF等[3]以方型钢管为研究对象,对钢管混凝土和钢管进行了静力加载和冲击荷载作用下的有限元分析和试验研究,通过分析动力和静力下的荷载位移曲线,得到了一种用加权平均数评定构件抗冲击承载力的方法．陈高哲等[4]进行了预加轴力下加强冷弯T型钢管节点的抗冲击性能试验,通过分析管节点在冲击荷载作用下的破坏模态、冲击力、位移时程曲线,获得了加强节点在冲击荷载作用下的工作机理．章琪等[5]采用有限元分析法,进行了不同类型的钢管混凝土跨中部位在冲击荷载作用下的仿真模拟,分析了各构件的抗冲击性能差异和破坏模式,得到增大钢管厚度可以提高抗冲击性能的结论．曲慧等[6-9]和陈凡[10]、王鹏[11]对T型管节点进行了试验研究和有限元模拟,分析了冲击力位移时程曲线,揭示了T型管节点抗冲击性能机理．曲慧采用有限元方法对设置加劲环和主管跨中局部加厚的T型管节点进行模拟,以研究加强措施对T型管节点抗冲击荷载产生的影响,研究结果表明:2种措施对T型管节点的抗冲击性能都起到了很好的加强效果．

目前,以上研究主要集中在对T型钢管节点的冲击力和支座反力方面上,研究中多数忽略了冲击荷载作用下T型钢管节点自身产生的惯性力．事实上,在冲击过程中,特别是冲击初始阶段,惯性力的影响是不可忽略的．因此,本文采用有限元模拟的方法,建立内置加劲环T型钢管节点有限元分析模型,通过分析主管跨中变形、冲击力、惯性力、支座反力时程曲线,揭示了T型钢管节点在冲击荷载作用下的工作机理．

1 有限元模型

1.1 典型分析模型的选取

为了比较加劲环厚度和宽度对T型管节点抗冲击承载力的影响,依据《钢结构设计规范(GB50017—2003)》[12]和管节点工程常用参数范围,根据李越[13]在T型管节点焊接残余应力分析研究中的模型,建立如图1所示内置加劲环节点．构件的几何参数如表1,模型编号中的字母RT代表内置加劲环T型管节点,D、T、L分别代表主管的直径、管壁厚度和长度;d、tz、l分别代表支管的直径、管壁厚度和长度;Rw和Rr分别代表加劲环的厚度和宽度．

表1 T型管节点分析模型参数

图1 T型管节点

1.2 材料特性

模拟过程中,取低速冲击速度8 m/s,选低应变率钢,因此符合Cowper-Symonds[14]模型,如式(1):

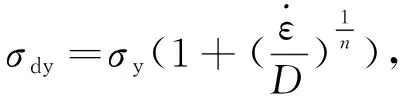
(1)

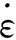
1.3 边界条件、界面处理、施加荷载

图2(a)给出了冲击过程中T型管节点的受力简图,图2(b)为有限元模型图．图中,主管左端U1、U2、U3、UR1、UR2、UR3 6个自由度完全被约束,用来模拟固定支座;主管右端放开U3,即沿主管轴线方向可以发生位移,用来模拟滑动支座．在右端设置弹簧,主管右截面和弹簧单元耦合,弹簧右端边界条件除水平方向位移外其他自由度均被约束．支管为自由端．

在模拟过程中,端板与钢管采用的连接方式为tie连接,冲击锤与支管端板的接触方式为通用接触,接触面的关系包括切向和法向2个属性．其中法向关系为硬接触,垂直接触面相互作用时产生的压力可以完全传递,当接触面分开时,产生的压力又完全消失;切向关系运用库伦摩擦模型模拟接触面之间产生的滑动摩擦,摩擦系数设置为0.3．另外,为了得到主管局部凹陷和位移受力情况,在进行网格划分时在主管跨中节点域范围内进行了网格加密处理．荷载的施加分为2个阶段．第一阶段,对主管施加轴力．利用有限元Abaqus的standard模块模拟T型管节点受轴力作用下的状态．轴力的施加是通过改变弹簧的压缩模量来实现的．第二阶段,对T型管节点施加动力荷载．将静力模型导入动力模型中并进行显示分析,同时为导入模型的锤头赋予速度和重力,以此研究重力、轴力、冲击力三者共同作用下的抗冲击性能．

图2 T型管节点受力和T节点模型

2 抗冲击性能分析

2.1 破坏模式

图3给出了3个内置加劲环T型管节点在相同的冲击荷载作用下最终时刻模型的整体变形模态和横剖面变形图．从3个节点的破坏形态来看,T型管节点的变形主要分为2部分:第一部分为冲击荷载作用下T节点的整体变形;第二部分为主管与支管相贯处发生的局部凹陷以及内置加劲环的变形．

T型管节点发生整体变形时,冲击荷载首先使撞击处出现局部凹陷,一部分冲击能量以应力波的方式向两端扩展,使主管发生整体弯曲．T型管节点发生局部凹陷时,支管端板承受强烈撞击,消耗大部分冲击能量,使主管和支管相贯处产生较大凹陷变形,而撞击区域以外虽然也发生变形,但明显弱于跨中撞击部位．冲击锤重量和速度的大小均可决定主管跨中冲击部位的破坏和凹陷程度．另外,构件承受冲击方向的主管厚度和加劲环失效都容易造成冲切破坏和局部凹陷[5]．通过比较图3(a)、(b)、(c)中各节点的凹陷和变形情况,可以得出加劲环厚度最小节点RT-2中,加劲环的变形和相贯处的凹陷是3个节点中最大的．由此可见,加劲环的厚度是影响T节点整体变形和局部凹陷的一个重要因素．

2.2 冲击力、支座反力、惯性力、跨中位移时程曲线

图4给出的是冲击力、支座反力、惯性力和跨中位移的时程曲线,其中,支座反力为2个支座处所测反力之和,各节点曲线趋势形状都基本相同．

图3 T型管节点的破坏模态

2.2.1 冲击力分析 图4(a)—(c)中各模型的冲击力时程曲线形状都基本相同,即:迅速达到冲击力峰值,然后又快速下降出现低谷,经过一系列震荡恢复平稳,最后降到零．峰值数值如图5．在初始阶段,T节点的冲击力时程曲线出现了一个瞬时峰值,在此时间段内曲线呈直线上升,从跨中位移曲线(图4(d))可以看出此时主管发生弹性变形．峰值过后,曲线开始急速下降,经过1～2 ms,冲击力达到谷值,如图4(a)—(c)．在此时间段内主管发生凹陷,刚度开始减小．随后在7～9 ms之间曲线出现了很明显的震荡,这是由于因为锤头的反弹、惯性效应和应力波在锤头之间来回弹射造成的[15]．T型管节点由于受到冲击荷载作用产生惯性力,并在冲击力峰值时刻,达到最大值,随后惯性力从最大值降到零后,出现一个反向的惯性力峰值,然后波动式地逐渐衰减到零,如图4(a)—(c)所示．在冲击力峰值时刻,应力波还未传递到支座处,并未产生支座反力来平衡冲击力．T型管节点为了保持动态平衡,自身产生惯性力来平衡冲击力,因此从图4(a)—(c)可以看出,冲击力峰值越大,产生的惯性力峰值越大．节点RT-3的冲击力时程曲线在2.63 ms时,达到峰值331 kN．节点RT-2的冲击力的时程曲线在2.4 ms时,达到峰值221 kN．节点RT-1的冲击力时程曲线在2.63 ms时,达到峰值280 kN．经过比较得知,在相同的冲击速度下,RT-3的冲击力峰值要大于RT-1峰值110 kN,RT-3主管跨中位移要小于RT-2 约为13 mm．RT-1的冲击力峰值要大于RT-2峰值60 kN,RT-1主管跨中位移要小于RT-2 约为30 mm．而在冲击试验中,冲击力的峰值与波形的持续时间受冲击点接触刚度有关,受冲击点接触刚度越大,所产生的冲击峰值也越大,波形的持续时间也就越短,变形也就越小[15]．因此可以得知:冲击力峰值越大,节点的刚度越大．节点刚度对结构的变形、内力以结构的整体稳定性都有一定的影响[16]．BOUWKAMP[17]利用三维有限元分析法,进行了节点变形性能对海洋塔架结构的影响效应研究,研究结果表明:节点刚度对于高于110 m的塔架的影响十分显著．HOLMAS[18]也利用数值分析方法进行了研究,研究结果表明:海洋工程结构的整体性能受节点刚度影响很大．通过分析冲击力峰值和跨中位移,可以得到不同内置加劲环参数对节点刚度影响很大,进而影响结构的抗冲击承载力性能．从图4可以看出节点RT-3的冲击力峰值最大,节点的跨中位移较小,所以刚度最大,所以节点RT-3抗冲击承载力性能较好．

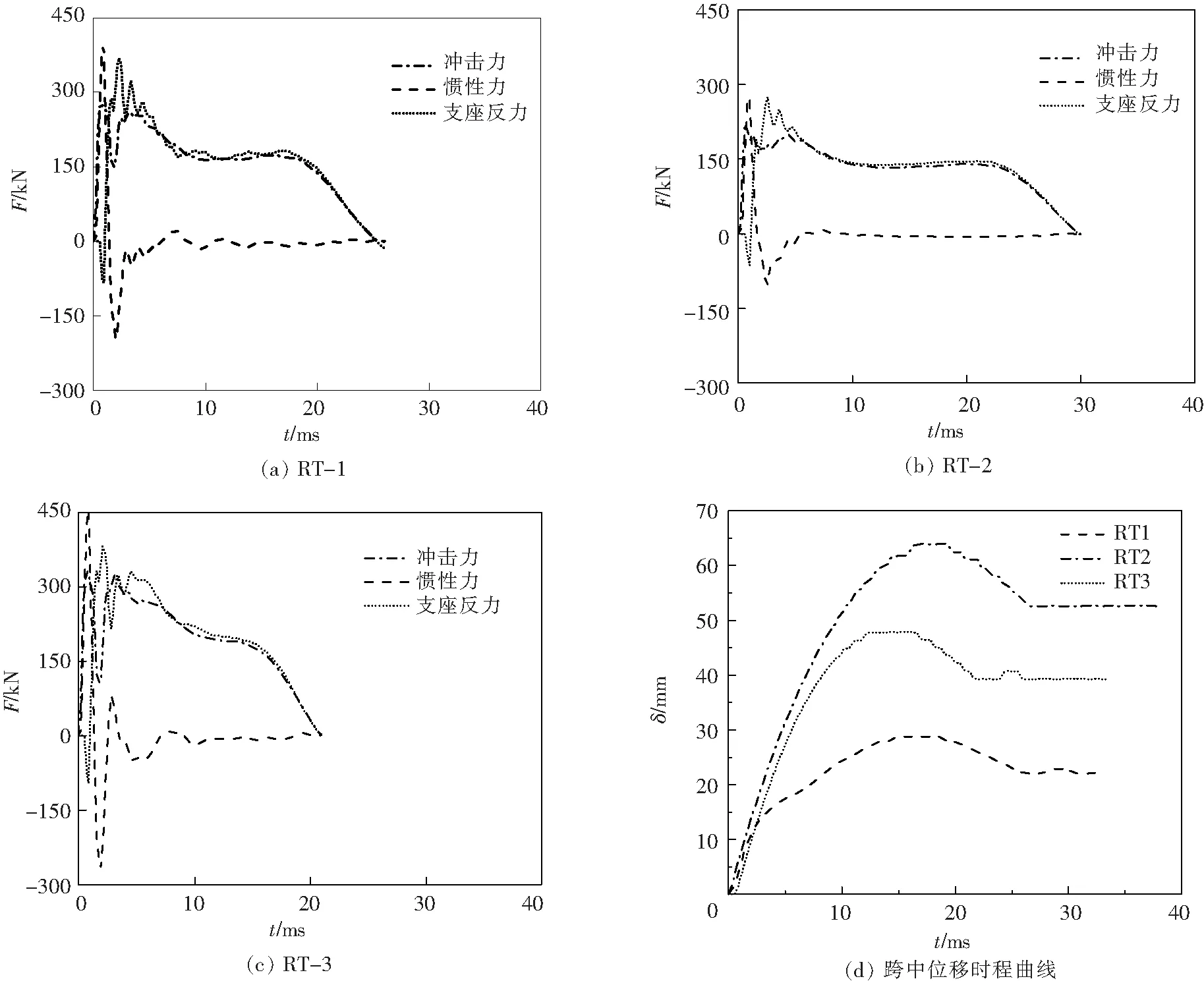
图4 冲击力、惯性力、支座反力、跨中位移时程曲线

2.2.2 支座反力分析 从图4(a)—(c)中可以看出:支座反力的时程曲线相对于冲击力是滞后的,首先出现一个瞬时负值,随后又迅速上升,达到峰值,过后开始一系列震荡,最后恢复到平稳状态直至支座反力合力衰减到零．在冲击荷载作用下,锤头与端板接触的一瞬间产生很强的冲击能量,输出的能量以应力波方式开始向两端支座传递．在传递过程中由于应力波互相干涉和叠加,节点的变形和外界对波产生的阻尼作用都会削减应力波的传递,所以当冲击力达到峰值时,应力波还并没有传递到支座,所以此时的支座并没有产生支座反力．但是在冲击力峰值时刻,支座反力时程曲线出现一个较小的负值,这是由于T型管节点受到锤头冲击时,因为惯性效应,支座两端具有向上运动的趋势,对主管施加的预压力得到释放,支座反力出现负值,随后支座反力快速增大至峰值[19]．

应力波通过梁传递到支座,并且产生拉力．随着应力波的持续的传递,冲击力点处的冲击能量开始削弱,应力波向支座两端传递的能量随着时间开始累积,当能量累积到最大值时,支座反力合力达到峰值．支座反力达到峰值时刻,由于冲击点处的能量减弱,冲击力减小,这时支座反力开始使节点失去平衡．为了保持节点平衡,惯性力从最大值降到零,随后出现的反向惯性力峰值和冲击力共同平衡支座反力．在冲击力平稳阶段,支座反力和冲击力平稳式衰减,并保持相对平衡,T型管节点处于相对静止状态,因此惯性力消失．

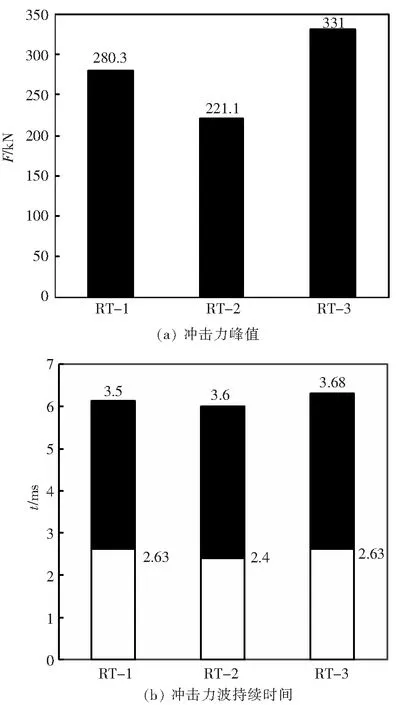
图5 冲击力峰值与波的持续时间

2.2.3 抗冲击承载力分析 通过冲击力时程曲线可以看出因为加劲环的参数不同,导致节点的抗冲击的性能和时程曲线也出现很大差异．首先,加劲环宽度相同的情况下,节点RT-3加劲环的厚度比节点RT-1增加了2 mm,冲击力时程曲线的峰值增加51 kN,平均每个单位厚度使峰值增加25.5 kN．将节点RT-2和节点RT-3进行比较分析,在加劲环厚度相同的情况下,节点RT-3加劲环宽度比节点RT-2增加了15 mm,冲击力时程曲线峰值增加110 kN,平均每个单位厚度使峰值增加7.33 kN．由此可见,加劲环对T型管节点抗冲击承载力的提高随厚度增大而增大,随宽度增大而增大．同时,还可以得出:加劲环的厚度对提升节点承载力的能力要明显强于宽度．

加劲环的设置可以增加节点的刚度,当受到冲击荷载时可以明显减少冲击过程中节点的局部凹陷和整体变形,因此在T型节点鞍点两端设置加劲环对提高节点承载力是有效的．通过冲击力、支座反力时程曲线分析也可以得到:冲击力峰值和波形持续时间与节点的刚度有关．峰值越大,峰值下降到低谷用的时间越短,刚度越大,节点的抗冲击承载力性能越好．支座反力的产生是由应力波传递冲击能量到达两端支座,传递的时间持续增加,支座处累积的能量越多,最后形成峰值．支座反力的峰值越大,两端支座处累积的冲击能便越多,间接说明节点跨中部位受到的冲击越大,在节点变形小的情况下,便可得出节点的抗冲击承载力性能越好．

3 结 论

通过以上分析,可以得到以下结论:

(1)在T型管节点鞍点两端设置加劲环可以提高节点的刚度和整体抗冲击承载力．在设置加劲环时,加劲环的厚度对提高节点抗冲击承载力的效果要强于宽度,因此可适当地增加加劲环的厚度或者减小主管的直径,都可达到增加整体刚度的效果．

(2)跨中位移,支座反力峰值,冲击力峰值和波形持续时间都可以反映T型管节点的刚度大小．峰值越大,波形持续时间越短,主管跨中位移越小,刚度越大,节点的抗冲击承载力越大．