地下水位上涨对典型明挖车站主体结构受力影响分析

王天水

(中铁大桥勘测设计院集团有限公司, 湖北武汉 430000)

华南地区地下水水位较高，地铁明挖车站一般在基坑降水后施工，为保证车站主体结构在施工过程中不产生上浮，车站主体结构在车站底板浇筑后一般会预留部分泄压井，待明挖车站完成覆土后再对泄压井进行封堵。地铁车站主体结构受力随着地下水位的变化随之发生改变。随着社会进步，目前双柱三跨车站较少，无柱车站因造价较高也相对较少，而单柱双跨车站较多；又常规情况下明挖车站一般为地下二层，故本文针对地下二层单柱双跨明挖车站进行分析。

1 工程概况

东莞地铁R1号线某二层单柱双跨明挖岛式车站，车站站台宽11 m，车站标准段外轮廓宽度为19.7 m，顶板覆土厚度3.8 m，地下一层结构净高4.95 m，地下二层结构净高6.21 m，车站顶板厚0.8 m，中板厚0.4 m，底板厚0.9 m，侧墙厚0.7 m。地质情况由上至下分别为杂填土层、素填土层、淤泥层、砂质黏性土层、全风化混合片麻岩层、强风化混合片麻岩层，车站底板位于强风化混合片麻岩层中(图1)。

图1 车站标准断面(单位：mm)

2 主体结构受力分析

采用SAP2000有限元软件分析地下水位在不断上涨过程中主体结构受力情况，以此来分析水位对车站结构的影响。为简化计算分析过程，将地下水位考虑由明挖车站基坑底以下1 m每次上涨2 m直至地面作为计算分析过程。车站主体结构受力计算采用荷载——结构模型进行计算，将横断面等效为宽度为单位长度的梁体系进行平面计算(即采用等效刚度法)，并建模时考虑板墙结合处的刚域效果。根据有限元计算原理，将组成结构的各段梁柱分成梁单元，各单元之间以节点相连。主体结构周边土体采用受压弹簧进行模拟，对于车站底板弹簧刚度大小取所在土层垂直基床系数，侧墙弹簧刚度大小取所在土层水平基床系数。结构计算时不考虑围护结构的作用，将荷载直接添加到主体结构上。

结构所承受荷载包括永久荷载、可变荷载，根据工程经验，地铁车站配筋控制一般为裂缝控制，故在本次计算分析中仅对准永久组合进行分析。

3 计算结果统计分析

针对结构计算中常用的计算节点统计出准永久组合值(表1～表4)。

表1 弯矩计算结果统计(一) kN·m

表2 弯矩计算结果统计(二) kN·m

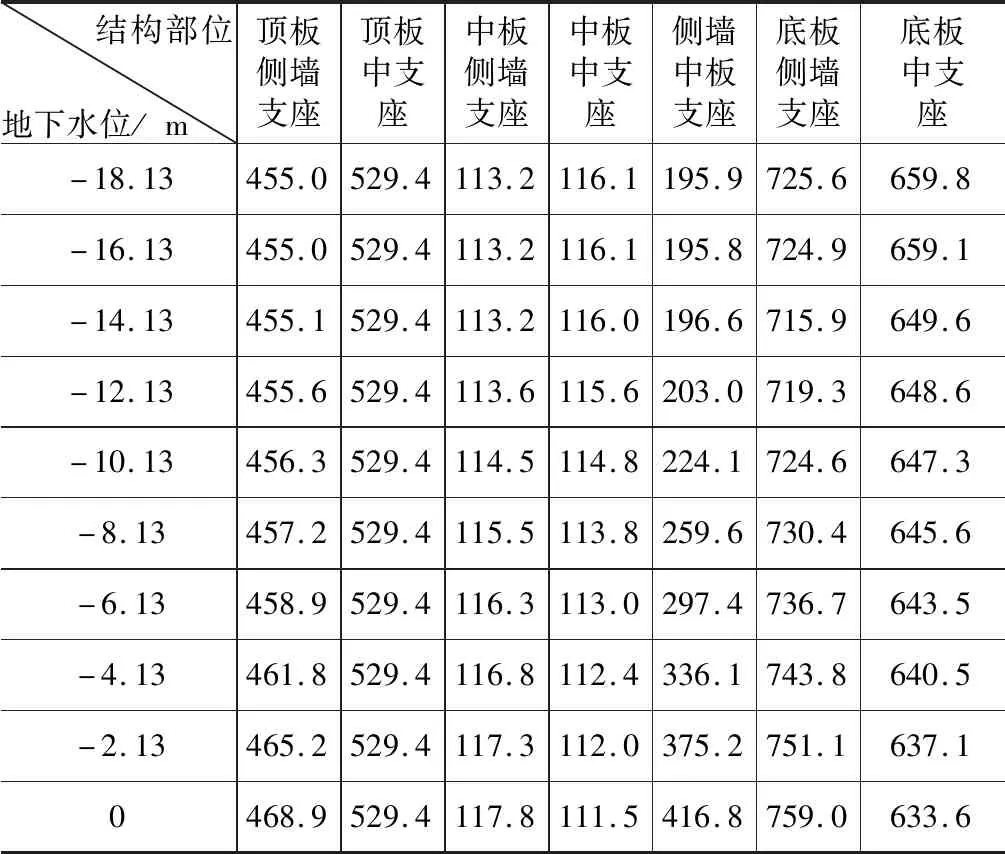
表3 剪力计算结果统计 kN

通过上述统计表格可以分析得出如下结论。

3.1 地下水位上升对构件弯矩值的影响

随着地下水位的上升，顶板侧墙支座、中板侧墙支座、侧墙中板支座、地下二层侧墙跨中及底板侧墙支座弯矩值随之增大；地下一层侧墙跨中、中板跨中、中板中支座、底板跨中及底板中支座弯矩值随之减小；顶板跨中及顶板中支座弯矩值不变。地下一层侧墙跨中、侧墙中板支座及地下二层侧墙跨中弯矩对地下水位变化比较敏感，最高水位弯矩值与最低水位弯矩值比值分别为0.44、3.11及1.95。

3.2 地下水位上升对构件剪力值的影响

随着地下水位的上升，顶板侧墙支座、中板侧墙支座、侧墙中板支座及底板侧墙支座的剪力值随之增大；中板中支座

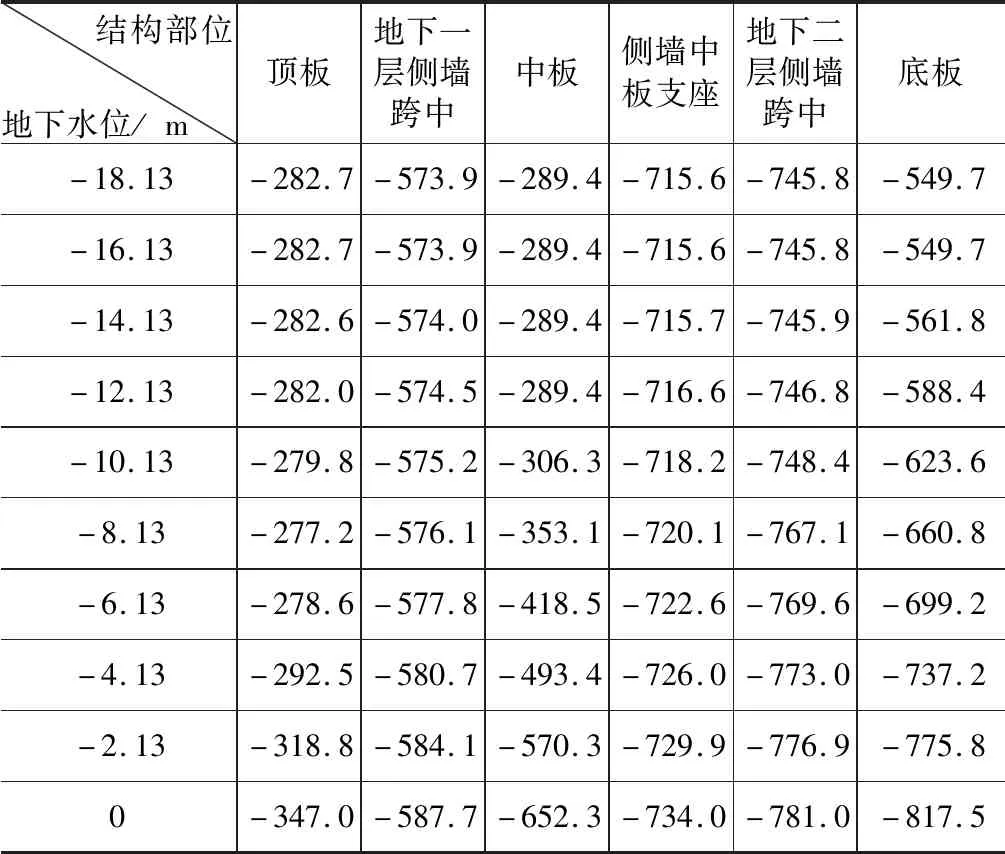
表4 轴力计算结果统计 kN

及底板中支座剪力值随之减小；顶板中支座剪力值不变。侧墙中板支座对地下水位变化比较敏感，最高水位剪力值与最低水位剪力值比值为2.13。

3.3 地下水位上升对构件轴力值的影响

随着地下水位的上升，顶板轴力值先减小然后增加，但减小幅度不明显(与最低水位工况对比减小约2 %)；其余构件轴力值均随之增大。中板及底板轴力对地下水位变化比较敏感，最高水位轴力值与最低水位轴力值比值分别为：2.25及1.49。

4 结论

本文通过对不同水位下二层双跨明挖地铁车站主体结构的受力分析，找出了各个构件内力随地下水位上升过程中的变化规律。大多数部位的结构内力随地下水位上升都有一定变化，除顶板轴力外，构件的内力最大值及最小值都出现在最低水位及最高水位工况，由于顶板轴力最小值变化幅度很小，可忽略其影响。但是为了保证设计质量并提高结构设计的工作效率，对于二层双跨明挖地铁车站主体结构的受力计算应采用最低水位和最高水位工况分别计算。