磁性石墨烯结构中自旋波的性质*

邱荣科， 王雪婷

(沈阳工业大学 理学院， 沈阳 110870)

磁性材料的研究和应用是当代凝聚态物理中的一个重要组成部分，随着科技的发展，器件小型化、微型化的需求使得低维磁性材料成为当前研究和应用的热点.以纳米材料中自旋波为基础的逻辑器件在尺寸减小、功耗降低和传输速度提高等方面具有显著的优势和广阔的应用前景[1].在过去的几十年里，各种磁性纳米结构(包括纳米线、纳米带、纳米盘、纳米薄膜等)的自旋波已被广泛研究.铁磁薄膜中的自旋波具有许多独特性质，可用于实现信号处理器件、逻辑运算器件和基于绝缘体器件的电信号传输，因此，铁磁薄膜中的自旋波在理论上和实践上得到了广泛研究.张光富等[2]基于微磁学模拟方法研究了磁纳米膜末端形状对自旋波模式特性的影响，分析了多种不同局域化、量子化自旋波的模式特性，且获得了末端形状对自旋波模式特性的调制规律.王焕等[3]发现在仅考虑近邻交换相互作用时，界面自旋波对外磁场和层间耦合具有较强的依赖关系.史晓霞等[4]采用二次量子化方法研究了面心立方结构铁磁性双层薄膜的性质，结果表明，无论界面为铁磁性界面交换作用还是反铁磁性界面交换作用，对称薄膜中的自旋波存在方式和整个能带形状均不受磁场和各向异性场的影响.Hog等[5]研究了自旋波谱和磁化强度随温度的变化关系后发现，薄膜上的自旋排列是非常不均匀的.Gruszecki等[6]利用微波电流在均匀纳米铁磁薄膜中产生自旋波束.Vladimirov等[7]以各向异性和各向同性准二维反铁磁海森堡模型为基础，研究了任意自旋波的激发谱，并计算了磁化强度的温度依赖性.Mamica[8]利用基于Heisenberg Hamiltonian的微观模型，研究了平行于薄膜表面的传播对自旋波谱的影响.本文试图从理论角度采用量子格林函数方法研究温度、外磁场和各向异性对铁磁单层石墨烯结构的自旋波谱和自旋波态密度的影响，从而总结各参数对磁性薄膜材料磁性的影响规律.

1 石墨烯结构模型和哈密顿量

采用单格点各向异性的海森堡模型研究磁性石墨烯结构的自旋波性质，具体模型与及其布里渊区如图1所示.由图1可见，石墨烯结构位于x-y平面上，其中A格点具有垂直于石墨烯表面的自旋，且具有铁磁性耦合，而B格点没有磁性.

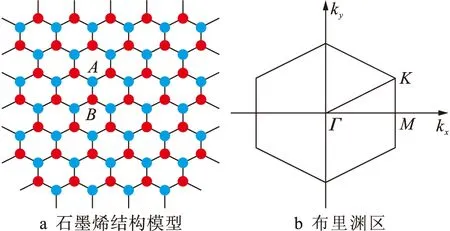
图1 石墨烯结构模型及其布里渊区Fig.1 Model for graphene structure and its Brillouin zone

哈密顿量可以表示为

(1)

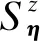
A格点的自旋初始方向沿z轴正方向，施加的外磁场B0也沿z轴正方向.A格点的每个最近邻自旋通过交换耦合作用进行铁磁性耦合.为了分析石墨烯结构的磁性质，根据文献[9]引入格林函数，其表达式为

(2)

式中：ω为自旋波频率；i1和i2为不同格点；S+和S-分别为自旋产生和湮灭算符；a为常数.

采用Tyablikov退耦近似交换耦合项，采用Anderson-Callen退耦近似单格点各向异性项.建立格林函数的运动方程，且格林函数的奇异点对应自旋波谱的解，具体求解过程参见文献[10-11].

自旋波态密度的计算表达式为

ρ(ω)=(-1/π)Tr·ImG

(3)

式中：Tr为矩阵的迹；ImG为格林函数的虚部.

此外，需要注意的是，当讨论磁性石墨烯结构的自旋波色散关系和自旋波态密度时，将自旋量子数S与层内交换耦合系数J均取为1，为了简化计算，其他物理量均取与层内交换耦合系数作比值后获得的约化数值(无量纲单位).

2 计算结果分析

图2为约化温度、外磁场和各向异性参数对磁性石墨烯自旋波频率的影响.图2a中外磁场磁感应强度B0=2，各向异性参数D=0.08，约化温度τ分别为0.1、0.5和0.9，且τ=T/Tc，其中T为温度，Tc为当系统参数取S=1、J=1、B0=0.1、D=0.08时的居里温度.图2b中D=0.08，τ=0.5，B0分别为2、4和6.图2c中τ=0.5，B0=2，D分别为0.02、0.05和0.08.

由图2可见，在布里渊区Γ-M和K-Γ中，随着波矢绝对值的增加，自旋波频率快速增加.在布里渊区M-K中，波矢从M点增长到K点，自旋波频率增长缓慢.由图2a可见，随着约化温度的升高，自旋波频率在整个布里渊区Γ-M-K-Γ中逐渐减小.约化温度对布里渊区中的M和K点的自旋波频率影响最大，在Γ点约化温度对自旋波频率影响最小.由图2b可见，在整个布里渊区Γ-M-K-Γ中，自旋波频率随着外磁场强度的增加而增加，在布里渊区M和K点磁场对自旋波频率的影响最大.由图2c可见，随着各向异性参数的增大，自旋波频率在布里渊区Γ-M-K-Γ中略有增加，但增加幅度很小，在布里渊区M和K点各向异性参数的改变对自旋波频率的影响最大.图2c中插图显示了经放大处理后布里渊区M-K中各向异性对自旋波频率的影响.

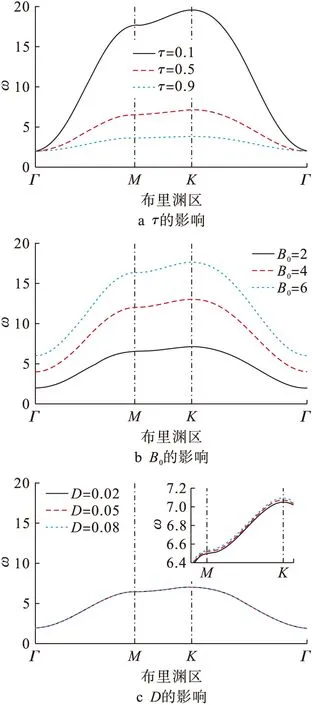
图2 自旋波频率随约化温度、外磁场、各向异性参数的变化

Fig.2 Change of frequency of spin waves with reduced temperatures，external magnetic field and anisotropy parameter

图3为在布里渊区Γ-M、K-Γ和M-K中约化温度对自旋波约化态密度(ρ/ρ0)的影响，其中ρ0是当系统参数取S=1、J=1、τ=0.5、B0=2、D=0.08时布里渊区Γ-M中态密度的第一个峰值.此外，图3中参数B0=2，D=0.08，τ分别为0.1、0.5和0.9.

图3a为在布里渊区Γ-M中约化温度对自旋波态密度的影响.当约化温度升高时，自旋波低频端频率几乎不变，高频端频率迅速减小，频率宽度减小.由图3a可见，自旋波态密度共有两个峰值，定义为峰1和峰2，且其频率分别对应自旋波谱中布里渊区的Γ点和M点.随着约化温度的升高，所有峰的强度均降低，且峰1的强度一直等于峰2.图3b为在布里渊区K-Γ中约化温度对自旋波态密度的影响.当约化温度升高时，自旋波频率变化与布里渊区Γ-M中的情况类似.由图3b可见，峰1′和峰2′的频率分别对应自旋波谱中布里渊区的Γ点和K点.随着温度的升高，所有峰的强度均降低，且峰2′的强度大于峰1′.图3c为在布里渊区M-K中约化温度对自旋波态密度的影响.当约化温度升高时，整个频带向低频端移动，频率宽度减小.由图3c可见，峰1″和峰2″的频率分别对应自旋波谱中布里渊区的M点和K点.随着约化温度的升高，所有峰的强度均降低，且峰1″的强度大于峰2″.

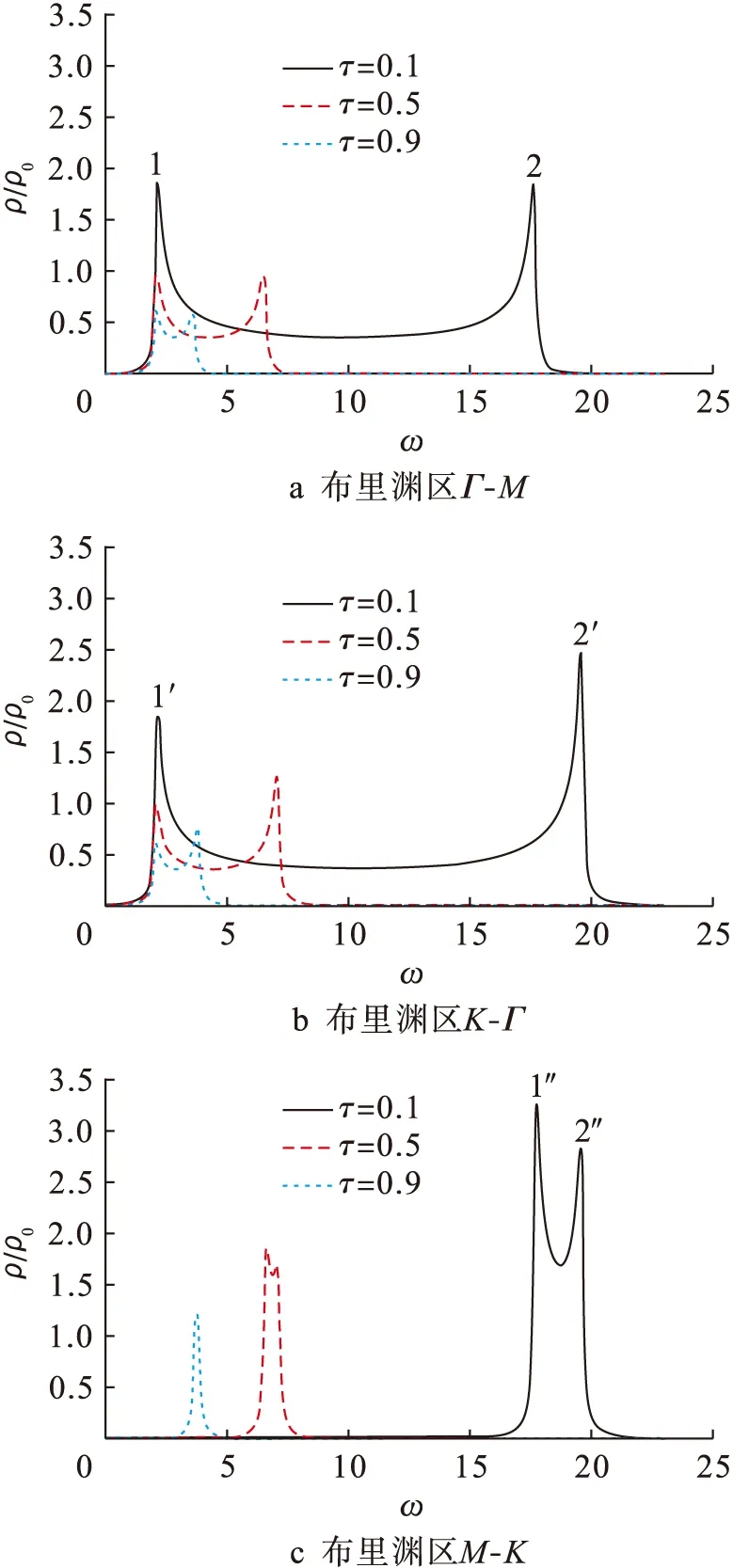
图3 自旋波态密度随约化温度的变化Fig.3 Change of density of states of spin waves with reduced temperature

图4为在布里渊区Γ-M、K-Γ和M-K中外磁场强度对自旋波约化态密度的影响.其中，参数D=0.08，τ=0.5，B0分别为2、4和6.

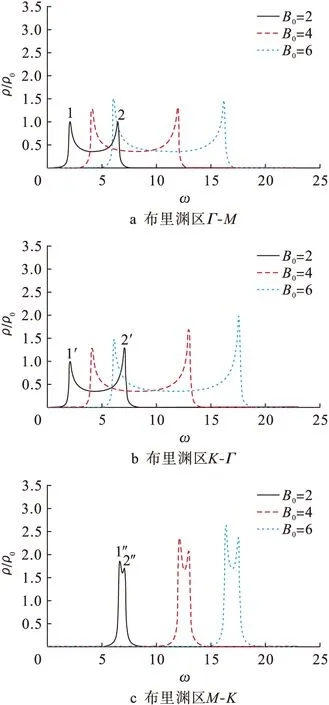
图4 自旋波态密度随外磁场强度的变化Fig.4 Change of density of states of spin waves with intensity of external magnetic field

图4a为在布里渊区Γ-M中外磁场强度对自旋波态密度的影响.当外磁场强度增加时，整个频带向高频端移动，且频率宽度增加.由图4a可见，峰1和峰2的频率分别对应自旋波谱中布里渊区的Γ和M点.随着外磁场强度的增加，所有峰的强度均增加，且峰1的强度一直等于峰2.图4b为在布里渊区K-Γ中外磁场强度对自旋波态密度的影响.当外磁场强度升高时，其自旋波态密度变化与布里渊区Γ-M中的情况类似.由图4b可见，峰1′和峰2′的频率分别对应自旋波谱中布里渊区的Γ点和K点.随着外磁场强度的升高，所有峰的强度均增加，且峰2′的强度大于峰1′.图4c为在布里渊区M-K中外磁场强度对自旋波态密度的影响.当外磁场强度增加时，整个频带向高频端移动，频率宽度增加.由图4c可见，峰1″和峰2″的频率分别对应自旋波谱中布里渊区的M和K点.随着外磁场强度的增加，所有峰的强度均增加，且峰1″的强度大于峰2″.

图5为在布里渊区Γ-M、K-Γ和M-K中各向异性参数对自旋波约化态密度的影响.其中，τ=0.5，B0=2，D分别为0.02、0.05和0.08.

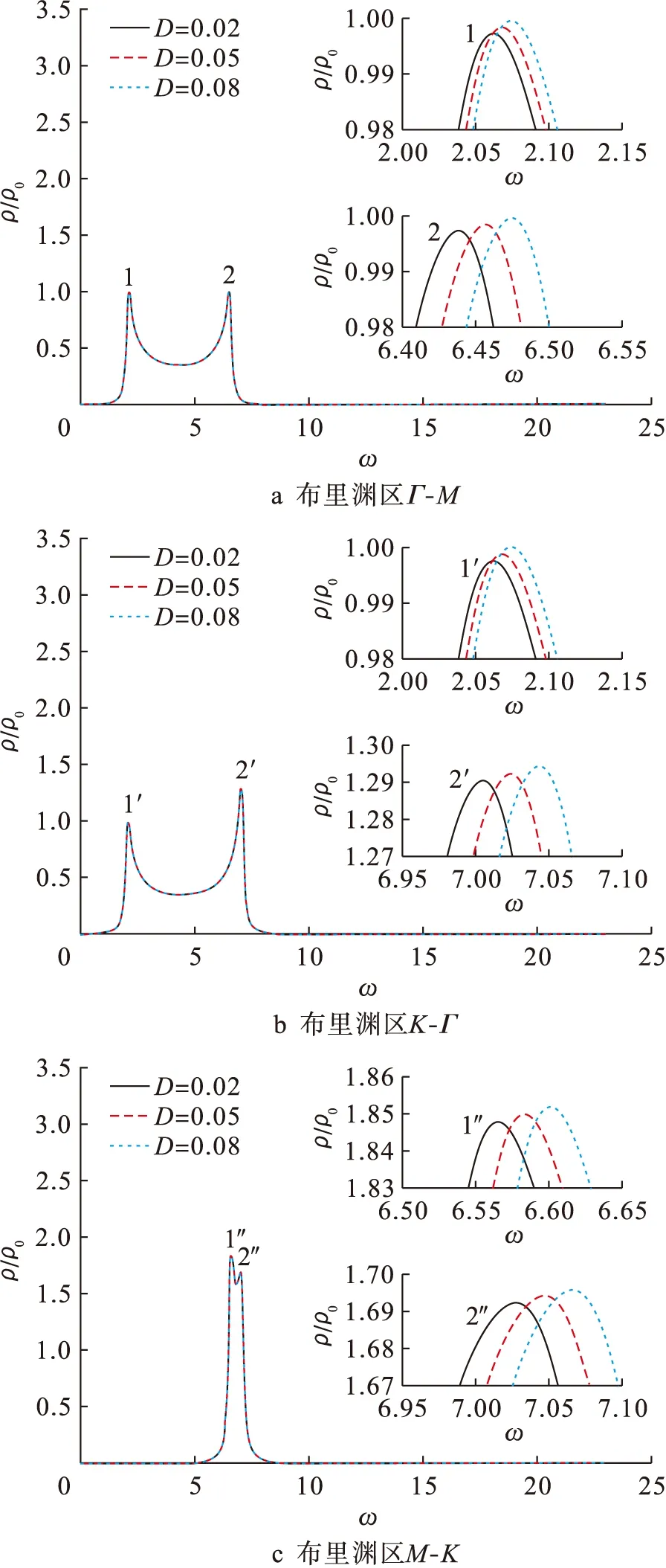
图5 自旋波态密度随各向异性参数的变化Fig.5 Change of density of states of spin waves with anisotropy parameter

图5a为在布里渊区Γ-M中各向异性参数对自旋波态密度的影响.当各向异性参数增加时，整个频带向高频端移动，但移动幅度微小.由图5a插图可见，随着各向异性参数的增加，所有峰的强度均稍增加，且峰1的强度一直等于峰2，且高频端移动幅度大于低频端移动幅度.图5b为在布里渊区K-Γ中各向异性参数对自旋波态密度的影响.当各向异性参数增加时，其自旋波态密度变化与布里渊区Γ-M中的情况类似.图5c为在布里渊区M-K中各向异性参数对自旋波态密度的影响.当各向异性参数增加时，整个频带向高频端移动，且移动幅度微小.由图5c插图可见，随着各向异性参数的提高，所有峰的强度均增加，峰1″的强度大于峰2″，且高频端移动幅度与低频端移动幅度相近.

3 结 论

采用格林函数方法讨论了温度、外磁场和各向异性参数对磁性石墨烯的自旋波频率和自旋波态密度的影响.随着约化温度的增加，低频端自旋波频率几乎不变，高频端自旋波频率减小，自旋波频率的宽度和自旋波态密度均减小，且变化幅度较大.在布里渊区Γ-M中，随着外磁场强度的增加，低频端和高频端自旋波频率均增加，自旋波频率宽度和自旋波态密度均增加.各向异性对自旋波频率和自旋波态密的影响较小.约化温度、外磁场强度和各向异性参数在布里渊区中的M和K点对自旋波谱的影响最大.