一类非线性偏微分方程组的行波解

邬家成，周 安

在过去的几十年里，非线性偏微分方程（PDEs）在各种研究领域［1］中被广泛研究，尤其是非线性偏微分方程解的数值方法.最近，人们对这种方法越来越感兴趣，这种方法可以帮助人们找出一些重要的非线性偏微分方程的精确解.随着数学的发展，数值解将在科学中发挥着重要的作用，甚至可以帮助人们找到新的现象.

随着学者们的探索，已经提出了求解非线性偏微分方程的各种方法.文献［2］中Tang、Lou提出了变量分离方法.同时，Feng在文献［3］中引入了一种新的方法—首次积分法，较其他传统方法具有许多优点.文献［4］中Wazwaz提出了sine-cosine法，文献［5］中Yusufoglu和Bekir验证了该方法的有效性.Evans等在文献［6］中应用了tanh方法.He、Abdou［7］和 Elwakil［8］及其合作者使用了改进的延拓tanh函数方法.Abdou［9］和Fan［10］分别在不同系统中应用了延拓的tanh-coth方法.Sheng［11］和Abdou［12］应用了F-扩展方法，一些非线性偏微分方程的解也可通过文献中的exp函数方法来求解［13］.我们还发现文献中的同伦扰动方法的一些研究成果［14］.Shao在文献中应用了人工可压逼近的方法给出了非线性偏微分方程解的性态［15］.

在本文中，我们使用首次积分法讨论了（2+1）维Chaffe-Infante系统ut-uxx-uyy+λ(u3-u)=0和phi-four系统utt-uxx-u+u3=0的行波解，并给出了一些结论.

1 基础知识

考虑非线性PDEs

其中，P是多项式.

首先使用波变量ξ=x+ay-ct对方程（1）进行变换，得到方程

若假设u(x,y,t)=U(ξ)，并引入变量

利用常微分方程定性理论与Division定理可得到（3）式的一个首次积分，将其代入方程（2）即可得到该方程的解，即得到非线性波动方程（1）的精确解.

定理 1（Division 定理）设P[ω,z],Q[ω,z]是C[ω,z]中的多项式，P[ω,z]在C[ω,z]中是不可约的.如果P[ω,z]=0 的零点也是Q[ω,z]的零点，则在C[ω,z]中存在一个多项式G[ω,z]，满足Q[ω,z]=P[ω,z]G[ω,z].

2 （2+1）-维Chaffe-Infante系统和phifour系统的行波解

在本节中，将基于首次积分方法来研究两个非线性PDE—（2+1）-维Chaffe-Infante系统和phi-four系统的行波解.

2.1 （2+1）-维Chaffe-Infante系统

首先考虑（2+1）-维Chaffe-Infante系统［2］

其 中 ，u=u(x,y,t),λ＞ 0 是 扩 散 系 数 .定 义ξ=x+ay-ct，（4）式可写成

再由（3）式可得

假 设X(ξ)和Y(ξ)是（6）和（7）的 解 ，是复域C[X,Y]中的不可约多项式，则

其中，ai(X)(i=0,1,…,m)是X的多项式，且am(X)≠0.方程（8）被称为（6）和（7）的首次积分.根据除法定理，在复数域C[X,Y]存在多项式g(X)+h(X)Y，使得

在这里，我们考虑了两种不同的情况，假设在（8）式中m值分别为m=1和m=2.

情形1假设m=1，通过比较（9）式两侧的系数相等，可得

由于ai(x)(i=0,1)是X的多项式，从（10）式可以推断出a1(X)是常数，为简单起见，取a1(X)=1 ，则h(X)=0 ，（11）式可写为（.12）式可写为（13）式.

平衡a0(X),g(X)的维数，只可得到deg(g(X))=1.设g(X)=AX+B，则a0(X)=，于是（13）式可写成

通过比较（14）式中X的所有系数，我们可以得到一个非线性方程组，通过求解可得

结合（8）式和（15）式，得到

再结合（6）式和（7）式，可得到（5）式的精确解

其中，ξ0是任意常数.则（4）式的精确解可以写

类似地，可得到（16）式～（18）式的精确解

情形2假设m=2，通过比较（10）式两侧系数相等，得到

因此得到a2(X)是一个常数，为简单起见，取一个a2(X)=1，从而（25）式，（26）式和（27）式可以写成

平衡a0(X),a1(X),g(X) 的维数，我们可得deg(g(X))=0或deg(g(X))=1.

I.deg(g(X))=0.设g(X)=A，然后a0(X)满足

通过比较（30）式中X的所有系数，可以得到一个非线性方程组，通过求解可得

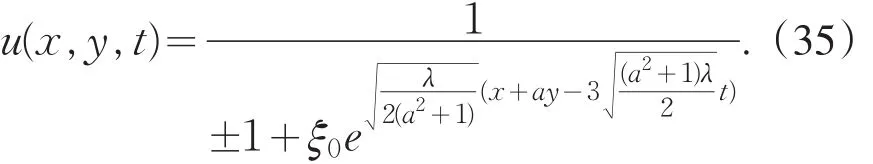
类似地，可以得到（34）式的精确解

II.deg(g(X))=1.设g(X)=AX+B(A≠ 0) ，从而可得

通过比较（27）式中X的所有系数，可以得到一个非线性方程组，通过求解可得

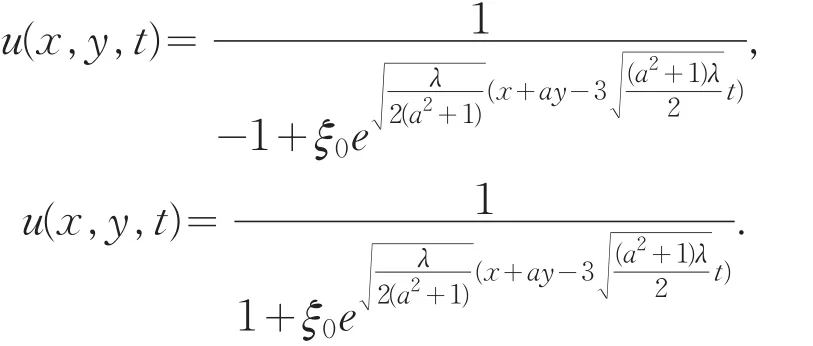
2.2 phi-four系统

接下来考虑phi-four系统［16］

假设u(x,t)=X(ξ)，其中ξ=x-ct.（41）式可以写成(c2-1)X″-X+X3=0，再由（3）式可得以 及设可写为

假设X(τ)和Y(τ)是（42）式的非平凡解.是复数域C[X,Y]中的不可约多项式，则其中，ai(X)(i=0,1,…,m)是X的多项式，am(X)≠0.由除法定理，在复数域C[X,Y]中存在多项式g(X)+h(X)Y，满足

在此考虑m=1,m=2两种不同的情形.

情形3假设m=1，通过比较（43）式两侧的系数相等，得到

由于ai(X)(i=0,1)是X的多项式，然而从（44）式可以推导出a1(X)是常数，为简单起见，取a1(X)=1 ，则h(X)=0 ，（45）式 可 以 写 为a′

0(X)(c2-1)=g(X),（46）式可写为

平 衡a0(X)和g(X) 的 维 数 ， 可 得deg(g(X))=1.不妨设g(X)=AX+B，从而有

通过比较（47）式中X的所有系数，可以得到一个非线性方程组，通过求解可得

情形4 假设m=2，通过比较Y′(ξ)两侧的系数相等，可得

由于ai(x)(i=0,1)是X的多项式，从（53）式可以推断出a2(X)是常数，为简单起见，取a2(X)=1，则h(X)=0，（54）式和（55）式可分别写 为和-2(X-X3)+a1(X)g(X)，（56）式可写为

平 衡a0(X)、a1(X)和g(X) 的 维 数 可 得deg(g(X))=1.不妨设g(X)=AX+B，从而有

通过比较（57）式中X的所有系数，可以得到一个非线性方程组，通过求解可得

3 结论

综上可知，首次积分法对于求（2+1）-维Chaffe-Infante系统和phi-four系统的精确解是一种可行的方法.因此该方法可用于解决更多其它该类型的非线性问题，并将在未来的数值计算中发挥重要作用，但该方法对有些类型的非线性PDEs并不适用.