摄像机标定系统方法研究
2019-07-19汪永超耿丽清
汪永超,耿丽清
(天津职业技术师范大学天津市信息传感与智能控制重点实验室,天津 300222)
随着计算机视觉技术的快速发展,计算机视觉技术已应用于社会的各个领域。其中,双目标定是立体视觉系统的基础,立体匹配和三维重建的准确性是由标定结果的准确性和速度决定的。因此,在双目立体视觉系统中,双目标定的准确性非常重要。摄像机标定可简单分为单目标定和双目标定,这是机器视觉的重要内容之一[1],相机标定有3 种常用的方法,分别为传统标定法、自标定法以及张正友标定法[2]。目前,传统标定法需要高精度的标定物,但在摄像机数学模型下计算十分复杂,标定速度慢;自标定法不需要借助参考物,但标定的精度和鲁棒性较低[3];而张正友标定法克服了传统标定法在标定物上的严格要求,并对自标定法进行了优化,具有标定精度高、操作简单、鲁棒性好等优点,被广泛应用[4-7]。本文在张正友标定法的基础上介绍利用OPENCV 软件实现的标定法,将该方法与MATLAB 软件双目标定进行对比,验证其标定法精度的准确性。
1 摄像机标定原理
在计算机视觉技术中,只有确定空间几何物体和它在图像中某一具体点和对应点之间的关系,才可以进行计算机视觉系统的下一步,因此建立几何数学模型是必要的,几何模型中的参数就是相机参数[8]。在一般情况下,相机参数的获取是由实验和相关数学计算得到的,而摄像机标定就是获得相机参数的过程,这个过程也被称为相机标定[9-10]。在几何数学模型下,实现将三维空间的某一个物体的坐标转化为二维图像下的坐标,需用到4 种坐标系,分别是世界坐标系、图像物理坐标系、像素坐标系和摄像机坐标系。相机标定中常用的坐标系如图1所示。

图1 相机标定中常用的坐标系
在图1中,像素坐标系(XfOfYf)和图像物理坐标系(XOY)之间的数学变化关系是以矩阵的形式实现,即:

式中:u,v 分别为像素坐标系中像素的横、纵坐标;1/dx、1/dy分别为图像物理坐标系中横、纵坐标的单位长度上的像素个数。
而世界坐标系(XwOwYw)和摄像机坐标系(xoy)之间的数学变化关系式为:

式中:T 为平移向量;R 为旋转矩阵。满足的约束条件为:

图像坐标系与摄像机坐标系之间的变化为:
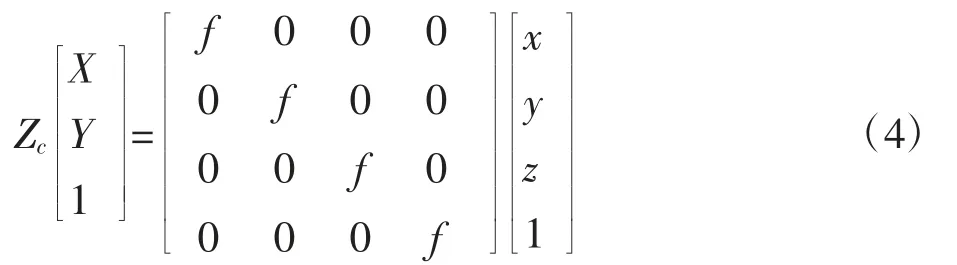
式中:Zc为摄像机坐标系(xoy)中的光轴,与x 轴和y轴互相垂直[3];X、Y 分别为某一点p 的摄像机坐标系在图像物理坐标系中的坐标;f 为相机的焦距。
将式(4)变化到像素坐标系,就可以得到点p 和像素坐标系下的像点pf之间的数学变化关系,从而可得到图像坐标系和世界坐标系之间的数学转换关系式[11]:

式中:M1为相机的内部参数,包含5 个,分别为1/dx、1/dx、f、u0、v0;M2为相机的外部参数,分别为旋转矩阵R 和平移向量T,共包含了6 个参数。
2 双目标定实验
本文所用到的标定原理是利用相机成像的几何数学模型,分别在MATLAB 和OPENCV 软件上进行标定实验。实验台如图2所示,标定的流程如图3所示。

图3 标定的流程
2.1 基于MATLAB的双目标定实验
采用张正友棋盘格双目标定法,使用MATLAB 的标定工具箱和棋盘格标定板对左右相机进行双目标定,获得相机的内部参数和外部参数。
在张正友棋盘格双目标定法中,通过选择不同方向、不同角度的棋盘格角点的2 个或多个图像,便可得出与成像平面对应的三维空间下的棋盘平面的坐标,然后就能得到2 个平面的单应矩阵H[12]。由式(5)与针孔成像可得:

式中:p 为成像平面的某一点的坐标;P 为三维空间下的坐标。将棋盘格转换到成像平面,可得:

根据式(6)和(7)推导出:

式中:H 为棋盘格与成像平面之间的单应矩阵,继而求出相机的内部参数M1、外部参数中的旋转矩阵R 和平移向量T。
基于MATLAB 的双目标定实验采用张正友标定法原理,其算法实现过程如下:
(1)在MATLAB 的命令行中输入stereo Camera Calibrator。
(2)选择上面的“Skew”“Tangential Distortion”以及“2 Coefficients”等选项,将“3 Coefficients”选项去掉。
(3)将采集到的图片信息进行标定。
(4)将标定后的结果进行保存[13]。
实验操作过程为:
(1)选择标定板:本实验所采用的的校准板为高精度浮法玻璃,如图2所示,其大小为340 mm×260 mm,每个方格的尺寸均为25 mm,图案阵列为12×9,其精度达到0.02 mm。
(2)采集图像:在系统过程中,相机保持静止的状态,采集校准板多组不同方向、不同位置的图像,同时将采集到的图像保存在项目目录下的toolbox_calib,保存的格式是bmp。
(3)角点提取:在MATLAB 工具箱中通过单击“提取网格角”提取每一个图像中的特征点,即每一个图像中的黑白棋格的交叉点。
(4)双目标定:对相机进行双目校准程序,用来获取相机相应的内部参数和外部参数。
(5)输出结果:内部参数采用矩阵的形式,如式(9),而外部参数采用旋转矩阵R 和平移向量T 形式。

2.2 基于OPENCV的双目标定实验
基于OPENCV 的双目标定实验同样采用的是张正友标定法原理,其算法实现过程如下:
(1)录入棋盘格的详细信息,包括棋盘格的横向和纵向的数目以及总的角点数目[14]。
(2)计算标定板上的实际物理坐标,通过采集到的图像信息进行亚像素角点检测。
(3)进行摄像机标定和校正。
(4)将标定后的相机的内部参数和外部参数进行保存[15]。
实验操作过程如下:
(1)选择标定板:选择、使用与MATLAB 校准板规格相同的校准板。
(2)采集图像:在系统过程中,相机保持静止的状态,采集校准板多组不同方向、不同位置的图像,同时将采集到的图像保存在项目目录下的calibdata,保存的格式是txt。
(3)角点提取:在OPENCV 中校准板中每个图像的角点由函数find Chessboard Corners 获得。
(4)双目标定:通过函数camera Matrix 和dist Coeffs获得相机的外部参数和内部参数[16]。
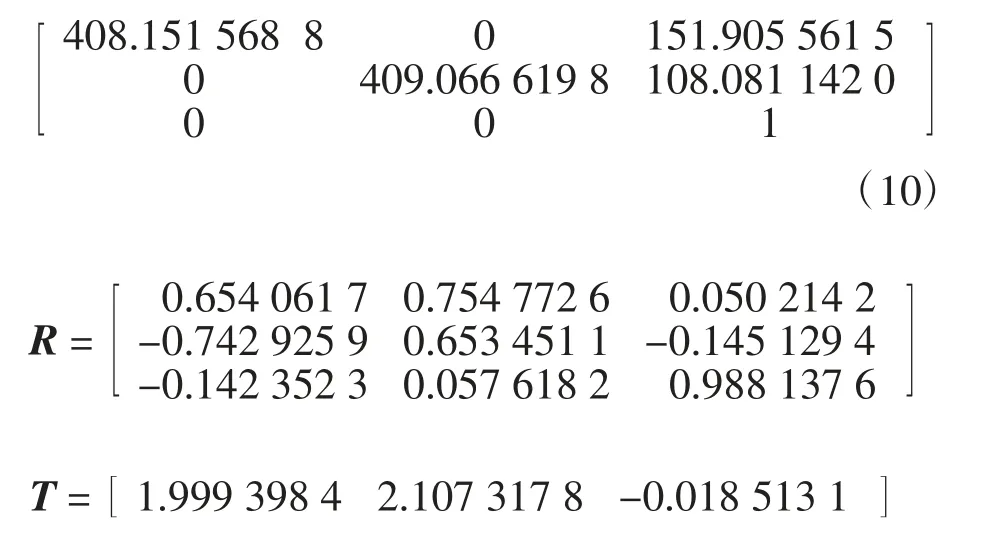
(5)输出结果:所获得的内部参数矩阵方程,如式(10)和外部参数平移向量和旋转矩阵。
2.3 双目实验结果分析
在实验中,采用的均是张正友标定法,相机的焦距为4 mm,相机的水平距离为20 cm,通过选取14 幅同一个相机、同一个校准板图像,获得相机的内部参数和外部参数。内部参数矩阵可以理解为焦距相关,它是一个从平面到像素的转换,焦距不变,内部参数也不变,所以确定后可以重复使用。畸变参数,一般也包含在内部参数矩阵中。而外部参数矩阵反映的是摄像机坐标系与世界坐标系的转换。从作用上来看,内部参数矩阵是为得到相机的信息并消除畸变,使得到的图像更为准确,外部参数矩阵是为了得到相机相对于世界坐标的联系,也是为了最终的测距。因此,通过式(9)和式(10)的相机内部参数比较得知,在外部环境一致的条件下,可以明显看到基于OPENCV 的双目标定比基于MATLAB 的双目标定结果更接近于实际相机的焦距,而且OPENCV 的双目标定结果更加精确。通过比较2 种标定结果的外部参数中平移向量T可以看出,基于OPENCV 的双目标定比基于MATLAB的双目标定结果更接近于实际相机的水平距离。
3 结 语
本文研究基于MATLAB 软件和OPENCV 软件,采用张正友标定法原理,对摄像机的标定系统结果进行准确性分析,得出摄像机的标定是为得到相机的内部参数和外部参数,内部参数主要是获得相机的焦距,外部参数主要是获得平移向量T 和旋转矩阵R,用来描述2 个坐标系之间的相对位置,所以相机标定结果的准确性影响双目立体视觉中测距的准确性。实验结果表明,在相同的外部实验环境、相同的标定法原理下,基于OPENCV 软件的双目标定的精度比基于MATLAB 软件的双目标定的精度更高,误差更小。
