一类系统谱的上界

吴 平

(苏州市职业大学 数理部，江苏 苏州 215104)

1 问题的提出

设Ω⊂Rm是一个逐片光滑的区域，考虑

的特征值的估计问题，其中n是边界∂Ω的单位法向量，谱又称特征值。假设

则问题(1)可写成矩阵形式。

设问题(2)的谱为0≤λ1≤λ2≤…≤λn≤…，对应的正交规范特征向量为u1，u2，…，un，…，即满足

根据分部积分，得

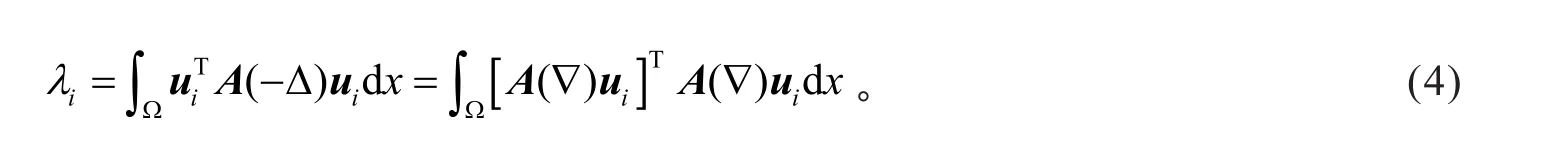
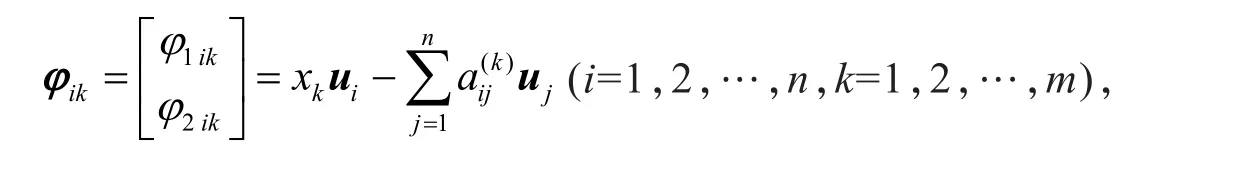
假设

式中

显然，φik与uj正交(i，j=1，2，…，n，k=1，2，…，m)，且满足

由Rayleigh定理，可得

计算得

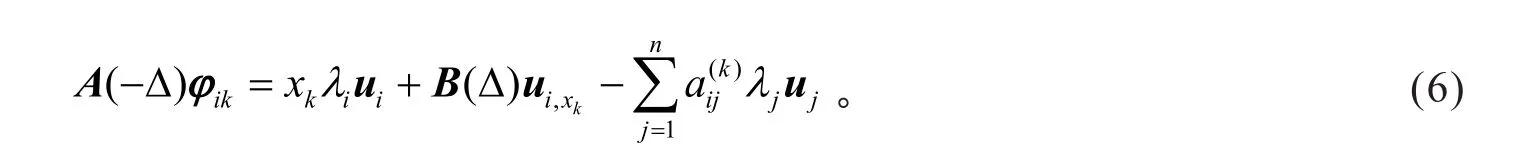
由φik与uj的正交性，及有

假设

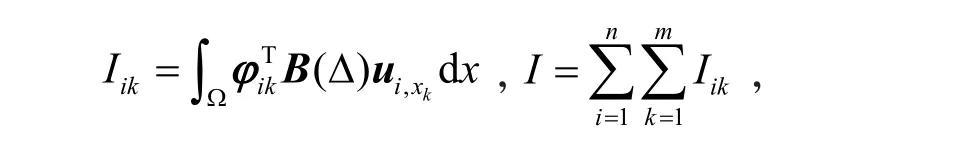
由式(7)，有

由式(5)和式(8)，有

2 主要引理

引理1设ui是问题(2)对应谱λi的特征向量，则

证明根据分部积分和式(4)，得

同理可得

由式(11)和式(12)，有

引理2设λ1，λ2，…，λn是问题(2)的n个谱，则

证明根据恒等式和分部积分法，得

由式(13)，有

由于

由分部积分，得

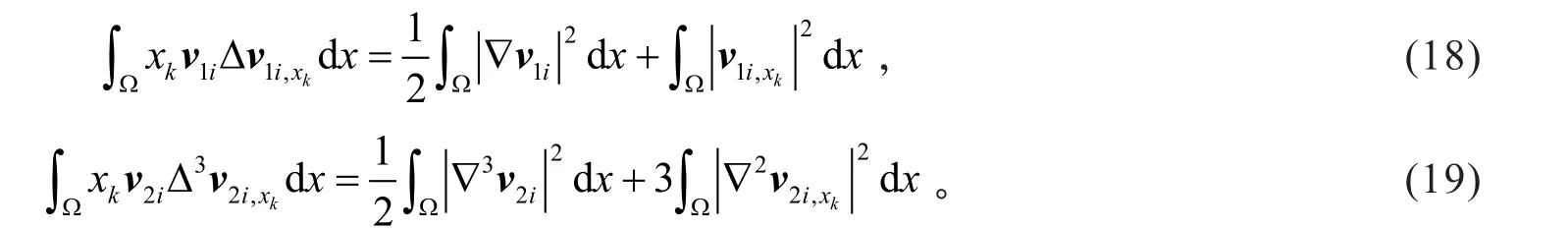
由式(17)、式(18)、式(19)和分部积分，有

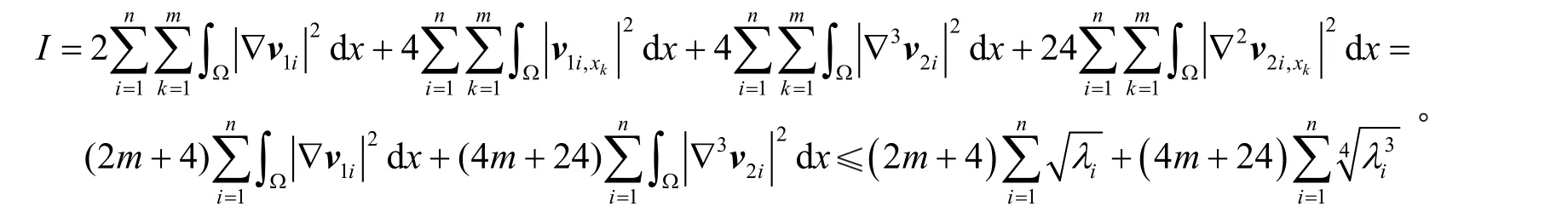
引理3对于φik和λi(i=1，2，…，n，k=1，2，…，m)，则

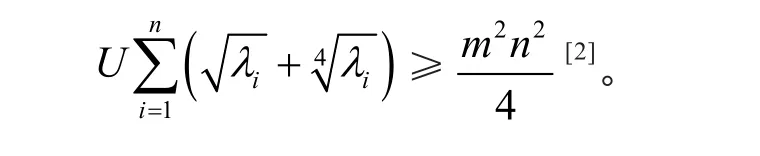
证明由φik的定义，有

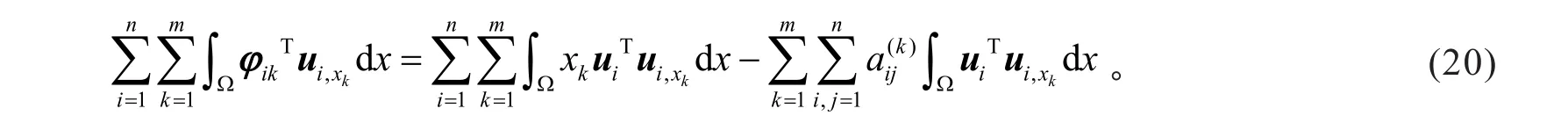
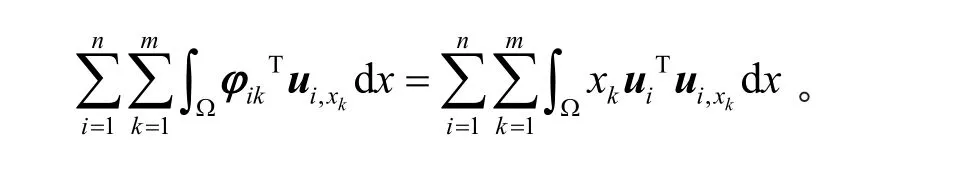
显然

由Schwartz不等式和引理1，有

3 主要结论

定理1如果λi(i=1，2，…，n+1)是问题(2)的谱，则

证明利用引理3，再利用式(12)和引理2，可得定理1的式(22)，在式(22)右端用λn替代λi，可得式(23)。

定理2对于n≥1，则

证明 选择参数σ＞λn，由式(9)，得

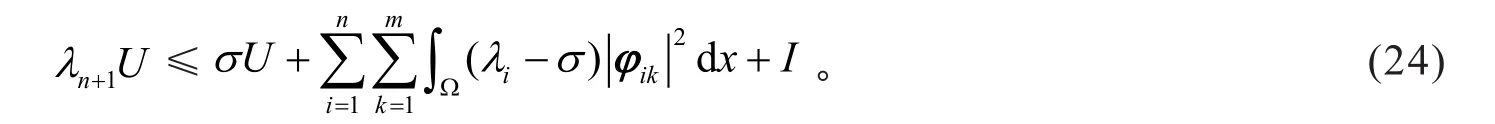
利用式(21)和Young不等式，得

式中δ＞0为待定常数。

为了使式(27)右端的值达到最小，取

将式(28)代入式(27)，得

根据引理2、式(26)和式(29)，得

式中σ＞λn，选择σ使式(30)右端等于0，即

假设

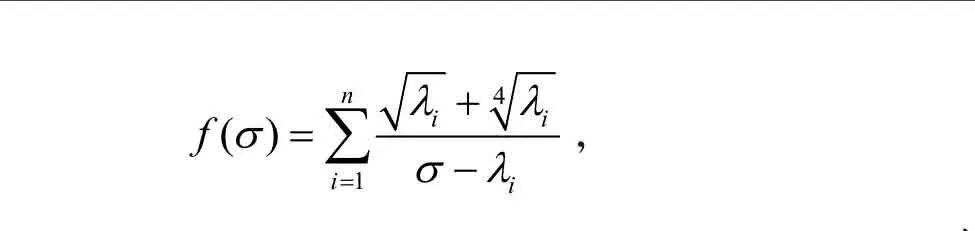
4 结论

方程的特征值问题是数学学科研究的一个重要领域，它所涉及的问题和内容复杂而广泛，本文研究了一类系统谱的上界估计，并得到了谱的上界的不等式，其结果在物理学和力学等领域中应用广泛。