基于双屈服条件准则的横观各向同性本构模型研究及其数值模拟

曲广琇，任鹏

基于双屈服条件准则的横观各向同性本构模型研究及其数值模拟

曲广琇1，任鹏2

(1. 贵州省交通规划勘察设计研究院股份有限公司，贵州 贵阳 550001；2. 中海地产中海发展(广州)有限公司，广东 广州 510600)

为研究层状岩体的力学特性，提出基于双屈服条件强度准则的本构模型。基于双屈服条件强度准则，联合横观各向同性的广义虎克定律刚度矩阵建立考虑横观各向同性的本构模型，并结合岩石单轴压缩试验数据，通过最小二乘法拟合该模型的参数；实现该模型的单轴压缩试验数值模拟，并通过室内单轴压缩试验结果对数值模拟结果进行验证，分析模型的可靠性。研究结果表明：本文提出的本构模型在层状岩体的力学分析方面具有适用性，为层状岩体力学特性研究及层状岩质边坡的稳定性分析奠定了基础。

横观各向同性；本构模型；双屈服条件强度准则；数值模拟

层状岩质边坡广泛分布于我国西南地区，其明显的横观各向同性力学特性对边坡的稳定性有着显著影响，因此如何建立适用的本构模型以探究其力学行为具有重要的工程实践意义。关于横观各向同性岩石的本构模型研究，国内外学者进行了大量研究。刘运思等[1]通过室内试验对横观各向同性岩体的弹性参数进行了研究。Gonzaga等[2]通过三轴压缩试验研究了如何确定横观各向同性岩石的力学参数。ZHANG等[3−5, 11]通过不同试验手段研究了横观各向同性岩石的破坏机理，探讨了加载速率对破坏过程的影响。熊良宵等[6−8]采用数值模拟方法，探讨了横观各向同性岩体的力学特性。Colak等[9−10]对横观各向同性岩体的破坏强度准则进行了研究。上述研究成果大都基于Hoek-Brown准则，描述横观各向同性岩体的强度和变形特征，并提出不同的强度准则和弹塑性本构模型，但大多研究成果仅从强度或者变形特征这种单一因素考虑横观各向同性岩体的本构模型，如何科学地描述层状岩石的强度和变形特征仍值得商榷。基于前人研究成果，并考虑层状岩体破坏受层理面影响显著的特点，本文提出基于双屈服条件强度准则，联合横观各向同性的广义虎克定律刚度矩阵，从应力、应变2个因素考虑，建立横观各向同性岩体的本构模型，并实现该模型的数值模拟的方法。通过室内单轴压缩试验结果对数值模拟结果进行对比，验证本文提出的本构模型及其数值模拟方法的适用性及可靠性，为层状岩体力学特性研究及层状岩质边坡的稳定性分析提供依据和参考。

1 横观各向同性岩石本构模型研究

1.1 强度准则建立

对于具有层状横观各向同性参数的岩石，Barton提出用双直线摩尔库伦剪切准则描述。针对层理状岩石的层面方向易发生滑移破坏的特性，提出层理面的强度参数c和φ比岩体部分的强度参数和小，如图1所示，图中压应力为正，层理面的强度直线与岩体的强度莫尔圆相交。

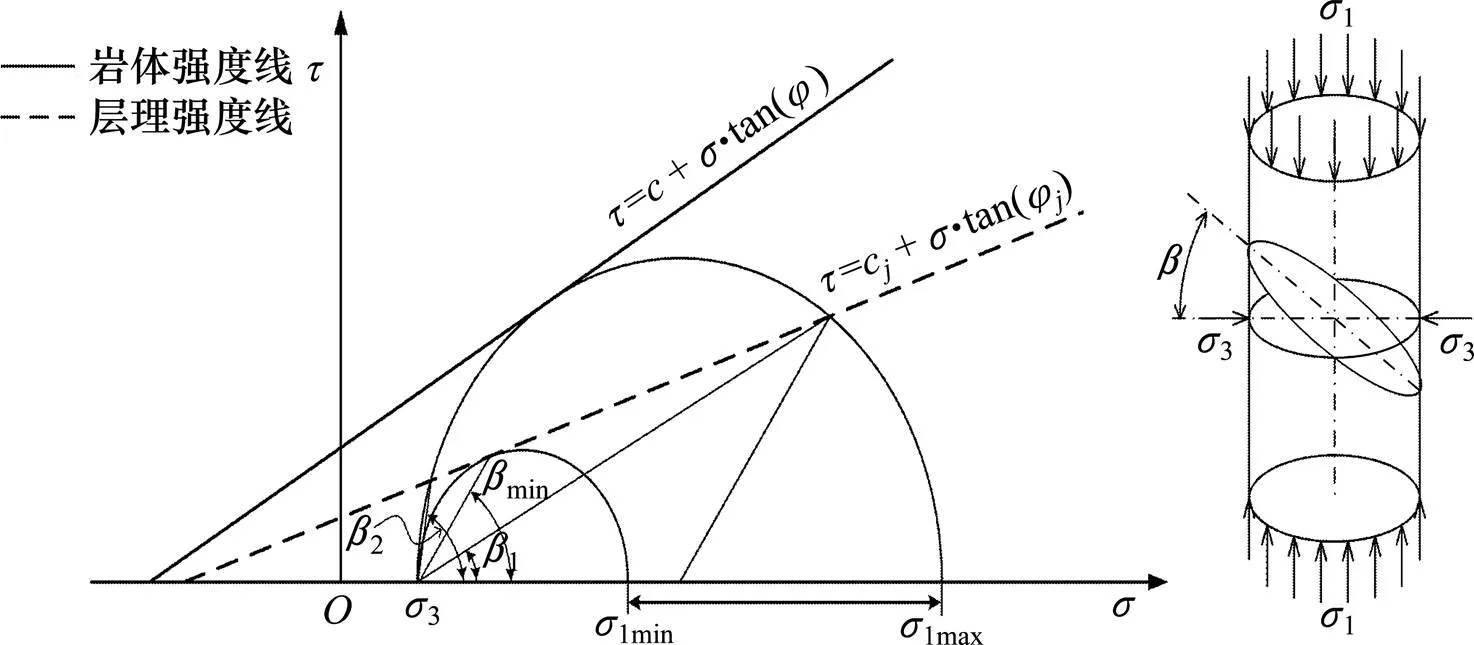
图1 层状结构岩石的双直线强度准则

对于没有层理面的岩体的任意角度面上应力状态如式(1)，此时的岩体强度满足式(2)所示准则：

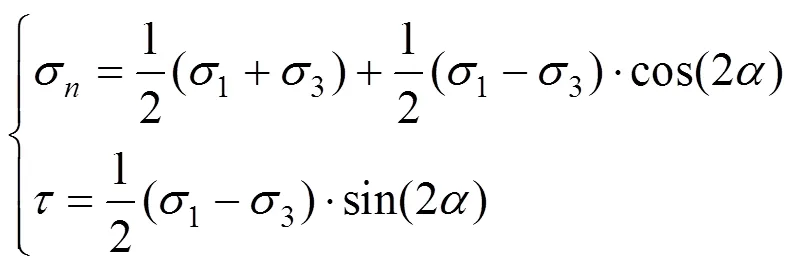
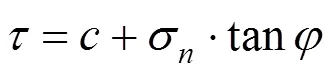
式中：σ为法向应力；为切向应力；1为最大主应力；3为最小主应力；为任意面与水平面夹角；为岩体的黏聚力；为岩体的摩擦角。

此时的破裂面倾角为：

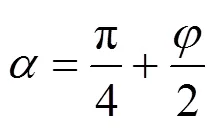
此时的最大主应力即岩体的抗压强度1max为：

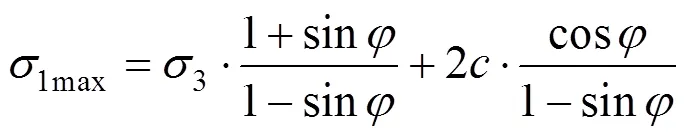
当岩体内存在层理面时，层理面上的破坏满足准则式(5)。如图1中虚线所示，当岩层面倾角1或2时，层状岩石的强度准则仍然遵循岩体部分的破坏准则，强度为1max；但是当1<<2时，层理面先与岩体的破裂面破坏，则强度由层理面控制，此时的破裂面=，则强度如式(6)：

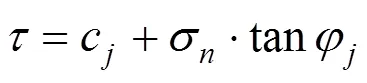
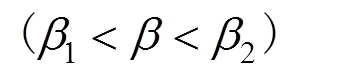
式中：c为层理面的黏聚力；φ为层理面的摩擦角；为层理面倾角；1β为层理面倾角为控制时的强度值。

将上式对求导，求得最小强度时的倾角为：

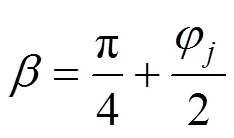
强度最小值1min为：

则压缩强度的范围为∈[1min,1max]，图中的1和2的点是指岩体和层理面同时破坏的情况，也就是岩体剪切与层理面滑移复合破坏。根据各个定义令1β1max,可求得1和2如式(9)，可以发现1和2的取值与岩体的强度参数、层理面的强度参数及围压有关。

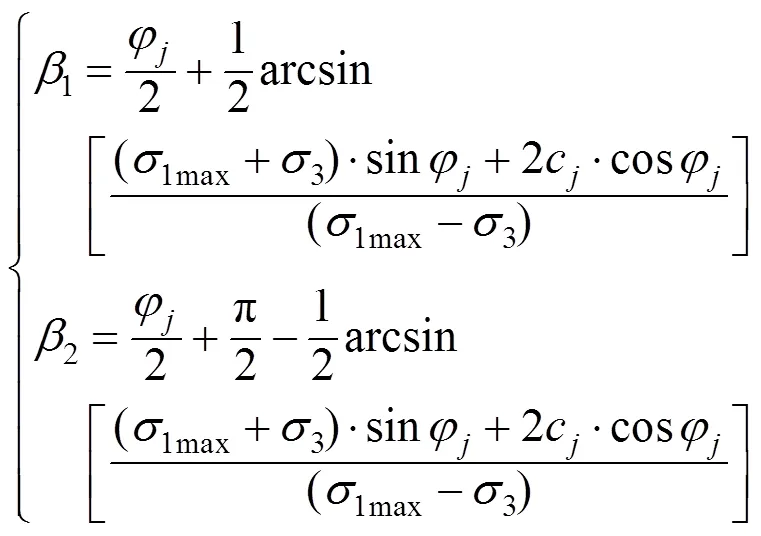
1.2 强度参数估计

基于上述强度准则，对于岩体的强度参数，一般可采用三轴试验，通过不同围压下强度莫尔圆，拟合公切线即可得岩体的强度参数，本文仅基于单轴压缩试验，根据式(3)和式(4)进行估计。统计不同倾角试样的破裂面倾角和单轴强度，如表1所示。统计数据表明0°，15°，30°和90°的主破裂面倾角相差较小，说明30°<1<45°，60°<2<90°。

为了估计岩体的参数值，求得的平均值66.125°代入式(3)可得：

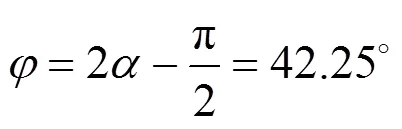
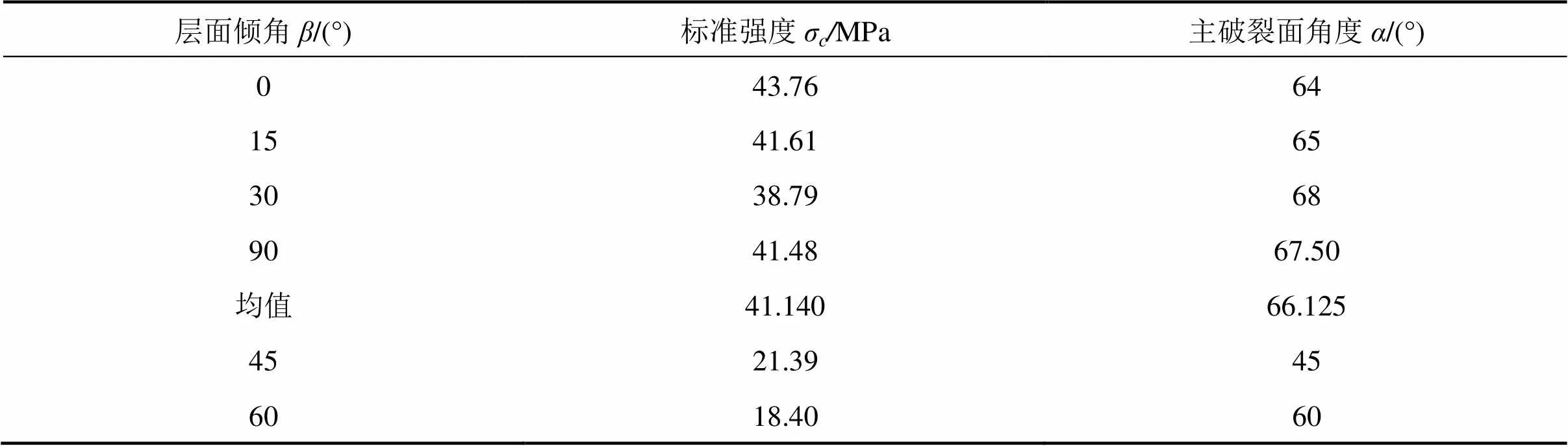
表1 不同倾角试样的单轴试验强度和破裂面倾角

此处为单轴压缩,则σ=0，将单轴强度的均值141.41 MPa代入式(4)可求得黏结力为：

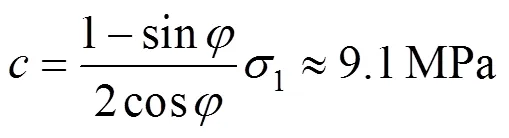
对于层理面的强度参数c和φ可根据式(6)求得，将层理面倾角为45°和60°的单轴抗压强度代入式(6)联立方程组为：

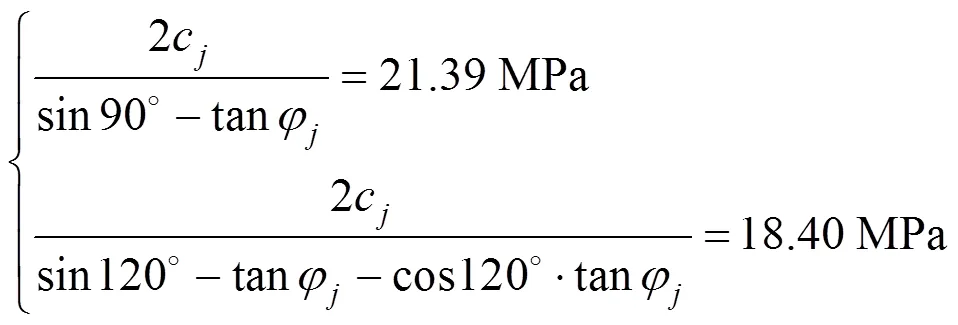
解得c=5.91 MPa，φ=24.10°。查阅相关地质手册，对于常见的板岩、页岩等层状岩石的内摩擦角在20°~55°之间，黏聚力在2~30 MPa之间，参数估计值在合理范围内。

1.3 横观各向同性本构模型构建

前文已建立了强度准则，但它仅能反映横观各向同性岩石的强度特征。为了反映横观各向同性岩石的变形各向异性特征，基于双屈服条件理论，引入横观各向同性广义虎克定律弹性刚度矩阵，建立基于横观各向同性强度和变形特征的本构模型。

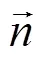
则局部坐标系σ′i′表示的应力分量可以通过旋转变换矩阵获得：

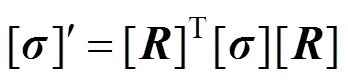
式中：[]为旋转张量；[]′为局部坐标系下的应力张量；[]为全局坐标系下的应力张量。

层理面方向上的切向牵引力分量，用表示，定义为：

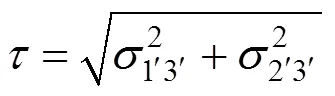
与之对应的应变分量为：

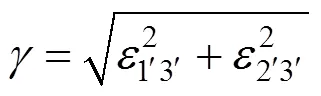
基于广义应力与应变分量的虎克定律的增量方程表达式为：

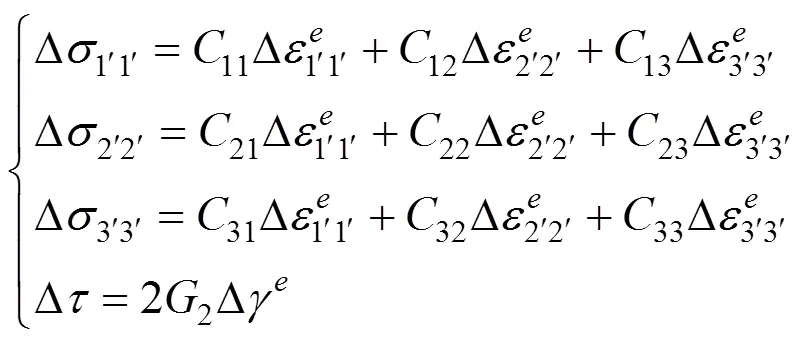
2 数值模拟

2.1 数值模型建立

为了验证横观各向同性的双屈服直线准则对层状岩石的适用性和优越性，拟采用单轴压缩数值模拟试验的方式验证强度和变形的各向异性特征，并与室内试验结果和理论计算结果进行比较。其中，室内试验为单轴压缩试验，本文仅提取试验结果，对试验过程不做累述。

本文的数值模型是基于FLAC3D技术针对横观各向同性本构模型进行的二次开发。对头文件(.h)和源文件(.cpp)进行修改完成后，将解决方案的C++环境调节到Debug和相应的操作系统版本(win32或x64)，如图3-8，将解决方案的配置属性中的调试命令设置为FLAC3D5.0安装目录下/exe64/ flac3d500_ gui_64.exe，将输出文件位置设置为FLAC3D5.0的安装文件夹下的exe64文件夹，则生成的动态链接库文件modetransubiquitl005_64.dll将自动保存至相应位置，点击调试按钮，生成解决方案，自动打开FLAC软件，通过config cppudm和model load modetransubiquitl005_64.dll加载完成调用调试。

计算模型采用与室内试验相同的圆柱体，尺寸为标准试件尺寸：直径为50 mm，高100 mm。试件层面倾角0°~90°，变化梯度为15°，建立的三维数值模型如图2所示。模型参数如表2所示。

表2 模型参数表

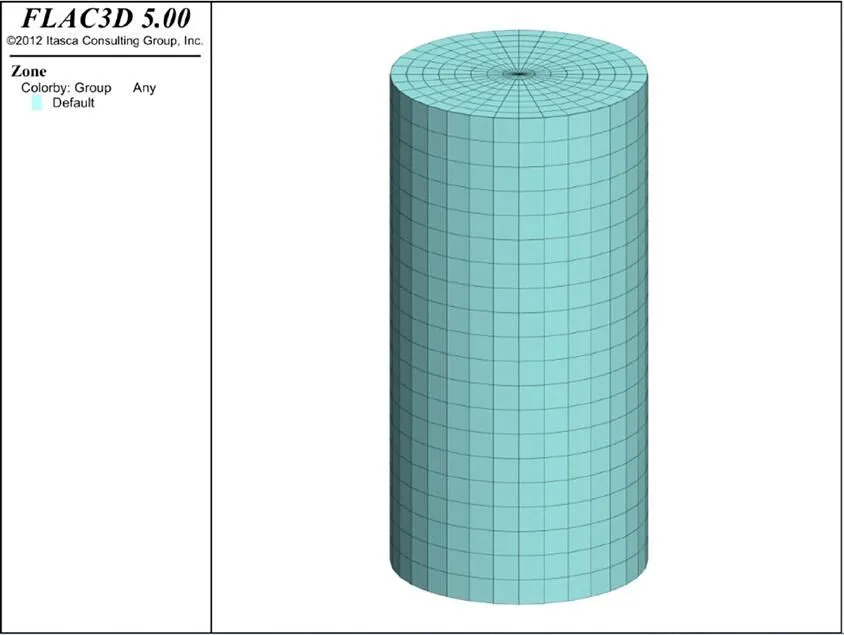
图2 三维网格模型

2.2 数值模拟结果分析

2.2.1 应力-应变曲线

图3数据表明：单轴压缩数值模拟的应力−应变曲线是遵循理想弹塑性体的变形关系。受力岩石前期弹性特征明显，屈服之前的应力−应变可简化为线弹性，这与数值模拟的结果相似，只是在压缩破坏阶段，室内试验结果岩石表现为脆性，而数值试验结果有一定的强度发展。图3还可以看出不同倾角的模型试验结果屈服强度各不相同，这反映了横观各向同性层状岩石强度的各向异性；观察不同倾角应力−应变曲线弹性阶段斜率，遵循变形特性的各向异性。所以从强度和变形2个方面验证了该本构模型的合理性、适用性和可行性。单轴压缩数值模拟试验结果数据见表3。

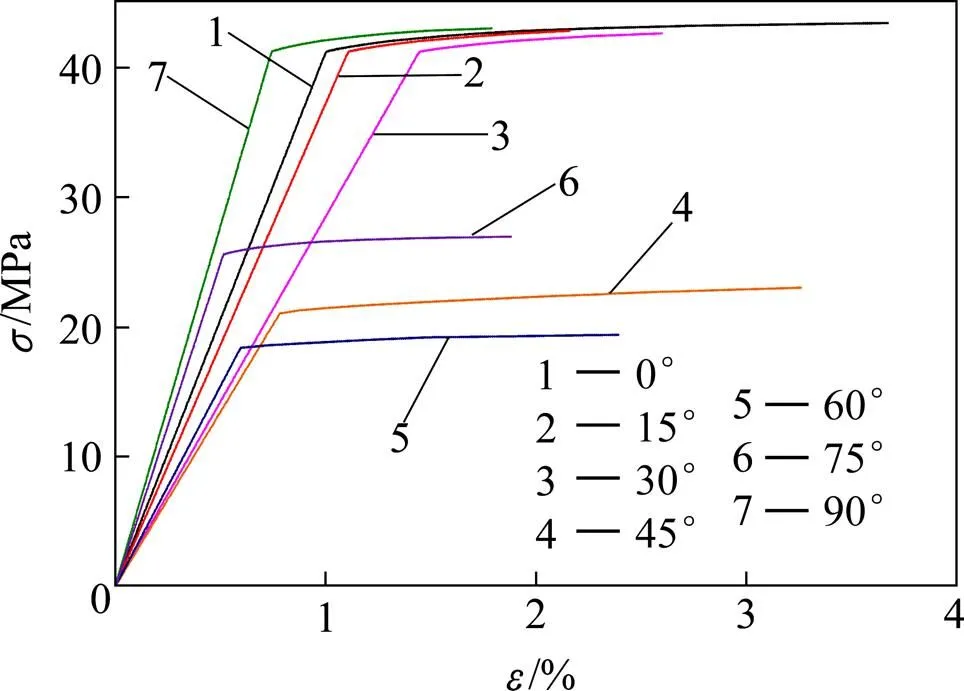
图3 不同倾角试样的单轴模拟应力-应变曲线

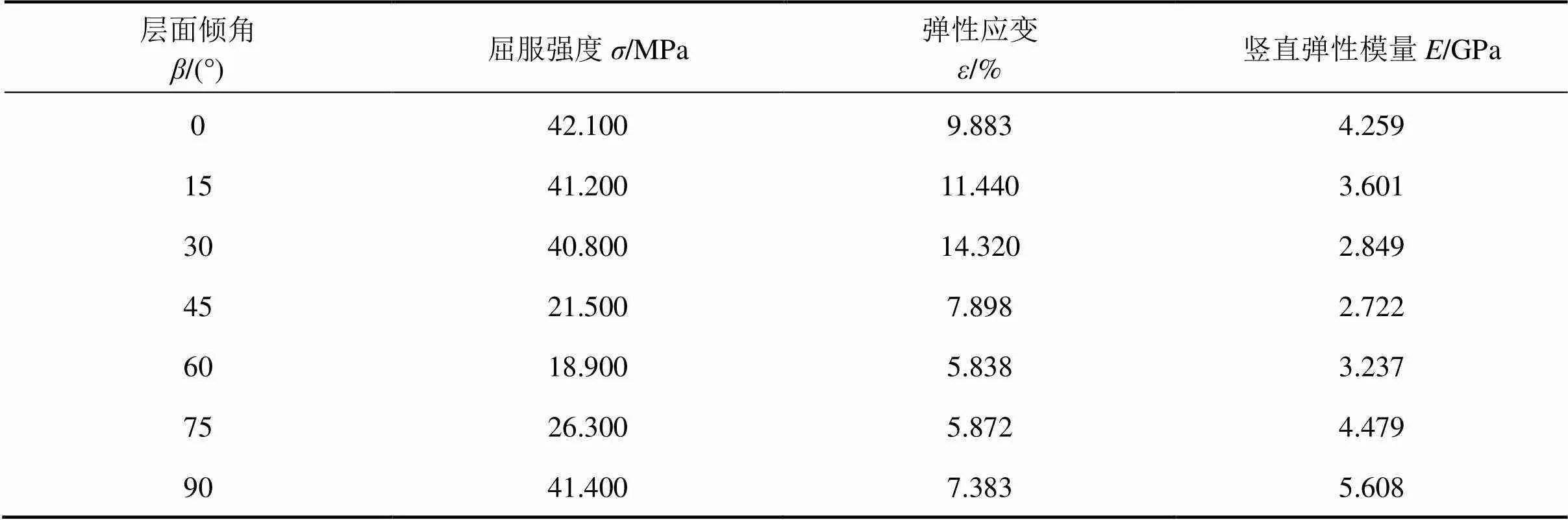
表3 单轴压缩数值模拟试验结果

2.2.2 压缩强度对比

对比室内实测单轴压缩强度和数值模拟计算结果见表4。两者相差较小，最大偏差=5.18%。由于相关参数是根据试验数据计算拟合得到的，所以相差较小，这也说明了双直线强度准则对该类层状岩石的适用性。

观察图4，将试验数据、模拟数据和理论计算曲线进行对比，理论曲线与模拟数据几乎重合，验证了数值模型的准确性。所以该本构模型能够反映该类岩石的强度各向异性。

2.2.3 视弹性模量对比

将表5中单轴数值模拟的视弹性模量与室内试验拟合曲线结果进行对比，见图5。数据分析表明：单轴模拟压缩的不同角度的弹性模量与拟合曲线基本吻合。然后，再对比单轴数值模拟的视弹性模量与室内试验值，偏差在8.32%的范围内，说明该本构模型能够反映弹性横观各向同性岩石的变形各向异性。

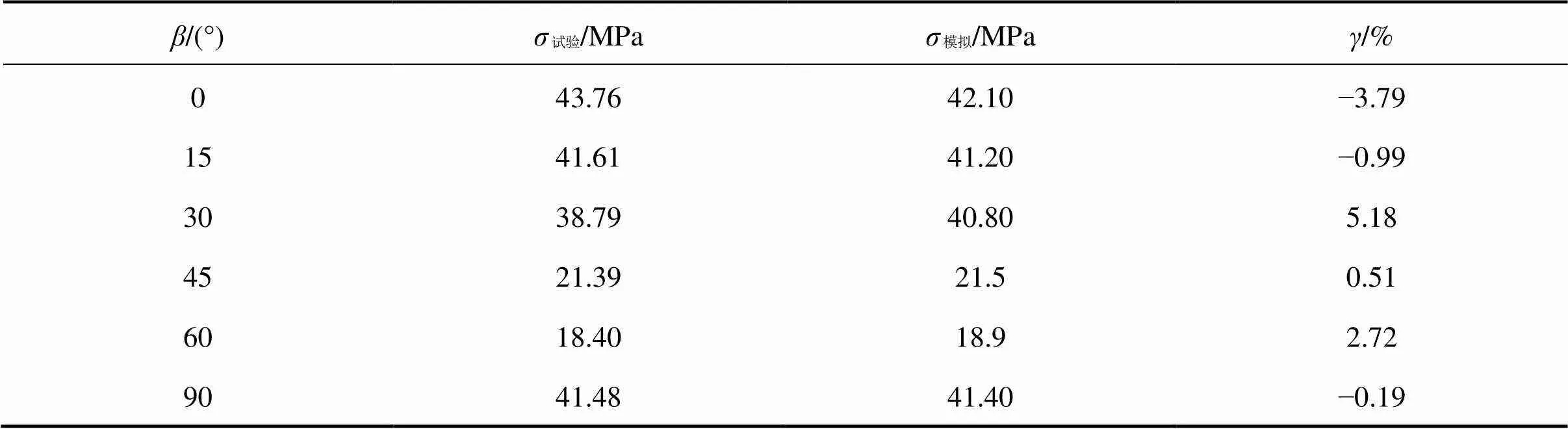
表4 数值模拟值与室内试验值对比

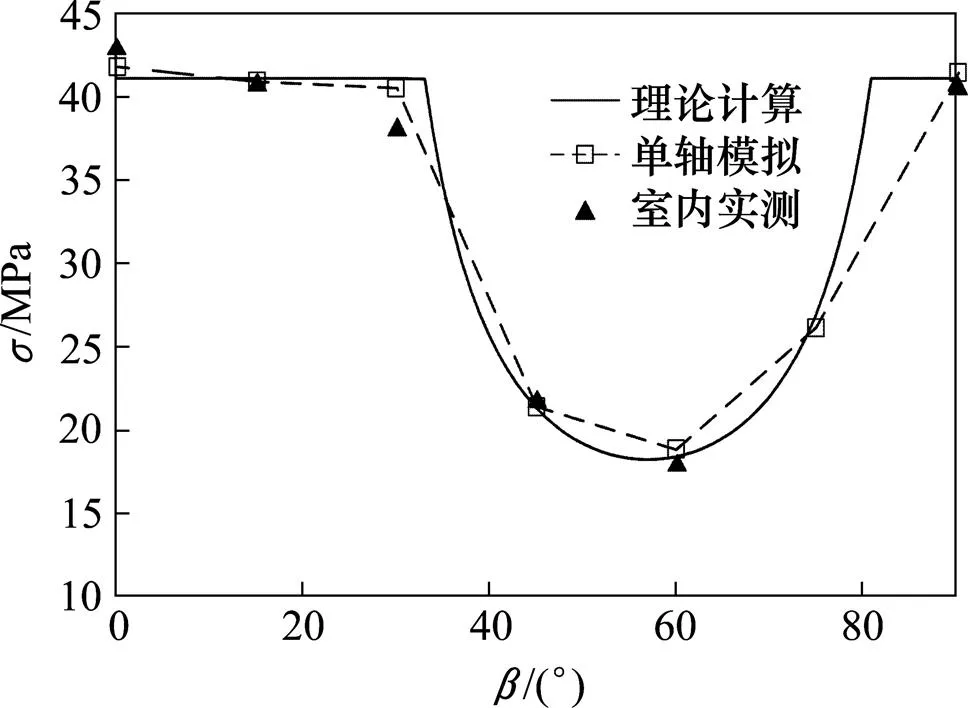
图4 单轴模拟、理论计算与室内试验强度对比图

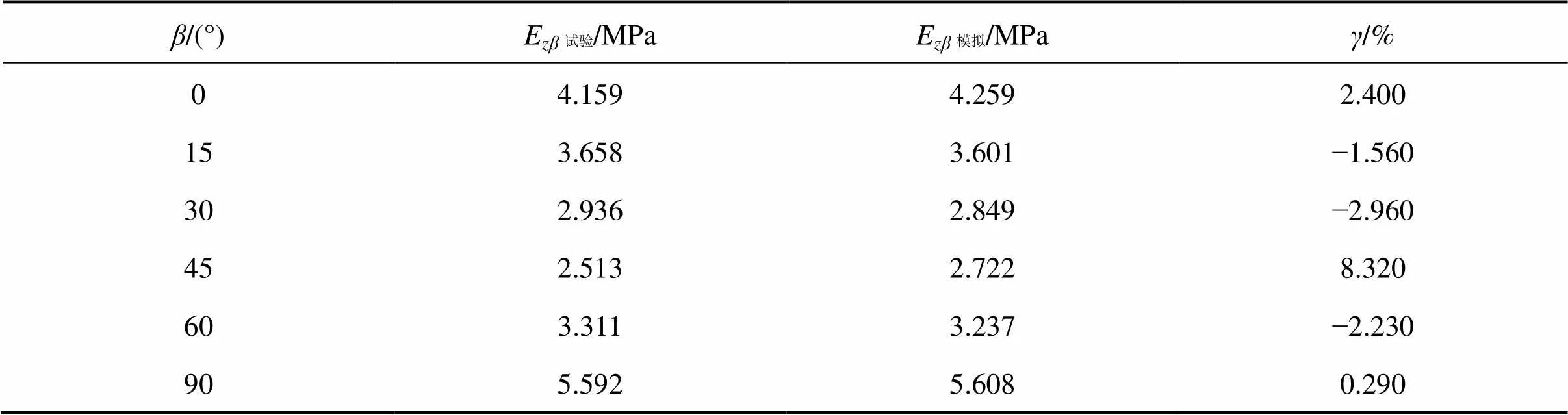
表5 数值模拟值与室内试验值对比

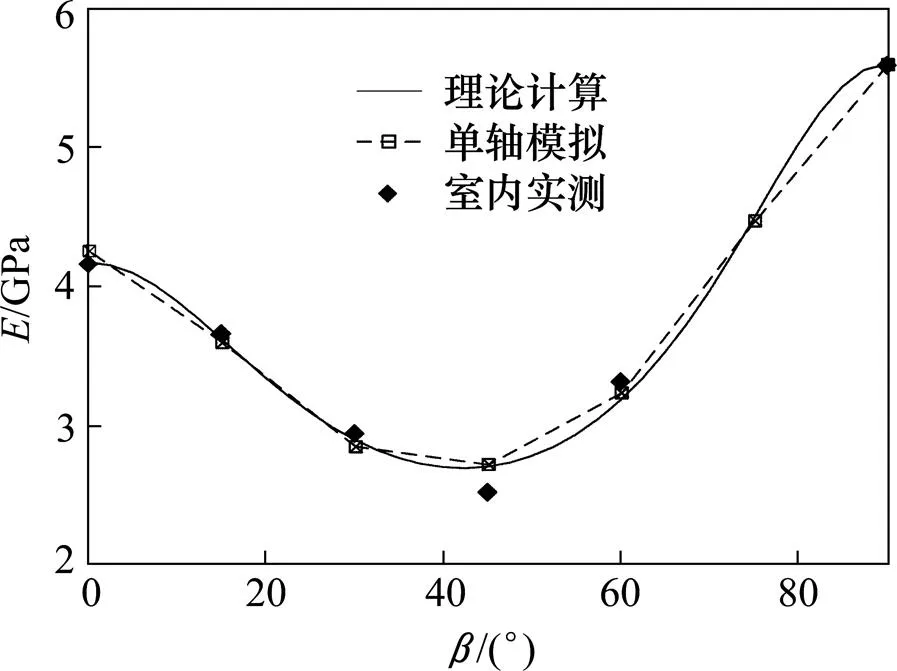
图5 单轴模拟、理论计算与室内试验视弹性模量对比

3 结论

1) 基于双屈服条件强度准则，结合横观各向同性的广义虎克定律刚度矩阵，从应力、应变2方面构建考虑横观各向同性的本构模型。

2) 建立基于双屈服条件准则的横观各向同性本构模型的数值计算方法，并通过室内试验结果对数值方案进行了验证。研究结果表明：本文提出的本构模型及其数值模拟方法可靠、适用。

3) 层状岩体的横观各向同性特征对边坡的稳定性影响相当显著。横观各向同性岩体通过影响层状岩质边坡的失稳模式进而影响其稳定性。工程实践中，必须对层状岩质的横观各向同性引起重视。

4) 本文并未考虑地下水对层状岩体的影响，对于物质组成中易发生软化的层状岩质边坡的稳定性分析，有待进一步探究。

[1] 刘运思, 傅鹤林, 伍毅敏, 等. 横观各向同性岩石弹性参数及抗压强度的试验研究[J]. 中南大学学报(自然科学版), 2013, 44(8): 3398−3404. LIU Yunsi, FU Helin, WU Yimin, et al. Experimental study of elastic parameters and compressive strength for transversely isotropic rocks[J]. Journal of Central South University (Science and Technology), 2013, 44(8): 3398− 3404.

[2] Gonzaga G G, Leite M H, Corthésy R. Determination of anisotropic deformability parameters from a single standard rock specimen[J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45(8): 1420−1438.

[3] ZHANG Jiuchang, ZHOU Suhua, FANG Ligang, et al. Effects of axial cyclic loading at constant confining pressures on deformational characteristics of anisotropic argillite[J]. Journal of Central South University, 2013, 20(3): 799−811.

[4] YONG M T, MING C K, JUANG C H. An experimental investigation of the failure mechanism of simulated transversely isotropic rocks[J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(8): 1163−1181.

[5] 范文臣, 曹平, 张科. 不同压剪应力比作用下节理类岩石材料破坏模式的试验研究[J]. 中南大学学报(自然科学版), 2015, 46(3): 926−932. FAN Wenchen, CAO Ping, ZHANG Ke. Experiment study on failure style of jointed rock-like material under different compressive-shear stress ratios[J]. Journal of Central South University (Science and Technology), 2015, 46(3): 926−932.

[6] 熊良宵, 李天斌, 杨昌斌, 等. 层状岩体单轴和双轴压缩蠕变特性的数值试验[J]. 吉林大学学报(地球科学版), 2013, 43(5): 1539−1548. XIONG Liangxiao, LI Tianbin, YANG Changbin, et al. Numerical analysis study on uniaxial and biaxial compression creep tests for interlayered rock mass[J]. Journal of Jilin University (Earth Science Edition), 2013, 43(5): 1539−1548.

[7] CAI M, Kaiser P K. Numerical simulation of the Brazilian test and the tensile strength of anisotropic rocks and rocks with pre-existing cracks[J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(41): 478−483.

[8] 梁正召, 唐春安, 李厚祥, 等. 单轴压缩下横观各向同性岩石破裂过程的数值模拟[J]. 岩土力学, 2005, 26(1): 57−62. LIANG Zhengzhao, TANG Chunan, LI Houxiang, et al. A numerical study on failure process of transversely isotropic rock subjected to uniaxial compression[J]. Rock and Soil Mechanics, 2005, 26(1): 57−62.

[9] Colak K, Unlu T. Effect of transverse anisotropy on the Hoek–Brown strength parameter ‘mi’ for intact rocks[J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(6): 1045−1052.

[10] SHI X, YANG X, MENG Y, et al. Modified Hoek–Brown failure criterion for anisotropic rocks[J]. Environmental Earth Sciences, 2016, 75(11): 995.

[11] YONG M T, MING C K. A failure criterion for transversely isotropic rocks[J]. International Journal of Rock Mechanics & Mining Sciences, 2001, 38(3): 399− 412.

A study of transverse isotropy model based on double yield conditions and its numerical simulation

QU Guangxiu1, REN Peng2

(1. Guizhou Transportation Planning Survey & Design Institute Co., Ltd, Guiyang 550001, China; 2. China Overseas Property Co., Ltd, (Guangzhou), Guangzhou 510600, China)

In order to study the mechanical properties of stratified rock mass, a constitutive model based on the strength criterion of double yield condition is proposed. Based on the strength criterion of double yield condition, the constitutive model considering transverse isotropy was established by combining the generalized Hooke's law stiffness matrix. The numerical simulation of the model was carried out, and the numerical simulation results were verified by the results of the laboratory test and the reliability of the model was analyzed. The results show that the constitutive model presented in this paper is applicable to the mechanical analysis of stratified rock mass and provides a foundation for the study of the mechanical characteristics of stratified rock mass and the stability analysis of stratified rock slope.

transverse isotropy; the constitutive model; double yield condition strength criterion; numerical simulation

TU458

A

1672 − 7029(2019)06− 1448 − 06

10.19713/j.cnki.43−1423/u.2019.06.013

2018−08−01

曲广琇(1982−)，男，吉林通化人，高级工程师，从事路基防护基础处理和工程造价等方面的研究；E−mail：58794826@qq.com

(编辑 涂鹏)