超高速磁浮车-轨道梁竖向耦合振动分析
2019-07-18倪萍许超超何军滕念管
倪萍,许超超,何军,滕念管
超高速磁浮车-轨道梁竖向耦合振动分析
倪萍,许超超,何军,滕念管
(上海交通大学 船舶海洋与建筑工程学院,上海 200240)
针对超高速磁浮车-轨道梁竖向耦合振动的问题,提出一种基于轨道梁有限单元模型和磁浮力比例-积分-微分(PID)控制器模型的分析方法。为提高计算效率,整体耦合系统以磁浮力为界,分为车辆和轨道梁2个子系统,车-梁之间的振动耦合则通过PID控制器计算的磁浮力来完成。组成耦合系统的子系统分别采用振型分解法和四阶龙格库塔法计算其振动响应。为验证方法的有效性以及了解超高速磁浮车桥耦合振动特性,使用Mathematica编程进行超高速磁悬浮车-轨道梁的耦合振动分析,得到运行速度为600 km/h的车辆和轨道梁的动力响应。研究成果可为超高速磁浮轨道结构设计和关键技术研究提供参考。
磁悬浮;600 km/h超高速;车−梁耦合振动;电磁力;PID控制器
磁悬浮列车是一种无接触的地面轨道交通系统,它以速度快、爬坡能力强、转弯半径小、经济环保等优势被认为是21世纪交通工具发展的方 向[1]。随着2016年长沙中低速磁浮快线的正式运营,我国磁浮技术实现了从研发到应用的全覆盖。在中低速磁悬浮列车[2−4]取得可喜研究进展的同时,国家也在对时速600 km的超高速磁悬浮列车的关键技术和设备国产化实施科研攻关[5],从而充分发挥磁悬浮列车高速运行的优势,开发超高速磁浮交通方式,拓展磁浮交通的应用领域。随着速度的明显提高,超高速磁浮系统对轨道的振动响应有更高的要求。近年来,国内外学者对磁悬浮车轨耦合振动进行了大量的研究。CAI等[6]以两质量块组成二系悬挂系统及简化移动荷载−轨道梁模型,分析了弹性轨道梁与高速磁浮列车耦合振动。时瑾等[7]以德国Transrapid高速磁浮铁路系统为基础,建立了高速磁浮车辆-轨道梁动力模型。詹旋裕[8]建立了二系悬挂的车桥耦合振动分析模型,对三跨刚构桥的动力性能进行仿真模拟。梁鑫等[9]对比了弹簧阻尼法和悬浮控制法2种磁轨关系对车桥相互作用的影响,仿真结果表明悬浮控制下的车辆具有更强的稳定性。SHI等[10]分析了加载不均匀周期性呈现对轨道梁振动的影响规律。YAU[11]通过分析得到车辆通过频率与轨道基频一致时出现轨道梁共振,反馈控制系数不影响共振速度但影响幅值的结论。REN等[12]将车辆模型等效为3种移动荷载模型和2种多自由的二系悬挂阻尼模型对Emsland线路动力响应进行分析。目前国内外大部分有关磁悬浮车桥耦合振动的研究,常将变化的电磁力线性化,把磁浮车辆等效为二系弹簧阻尼质量块模型。然而磁浮车桥系统之间的振动是由控制系统进行调节,这是一个磁浮车辆系统-悬浮控制系统-桥梁系统三者之间的耦合振动问题。磁轨关系是磁浮车桥相互作用最基本、最关键的问题。因此在分析磁浮车桥耦合振动时,为更符合实际情况应充分考虑到电磁力的变化和系统的不稳定性,引入悬浮控制,对磁浮系统实现闭环控制。为此,本文引入PID控制器对电磁铁系统进行主动控制,将整个车桥系统在磁轨接触处划分为车辆和轨道梁系统,分别建立每节车厢10个自由度的磁浮车辆模型和有限元轨道梁模型,仿真模拟时速600 km的磁悬浮车桥耦合竖向振动,希望为超高速磁浮轨道结构设计和关键技术研究提供参考。
1 磁浮车辆竖向振动模型
德国TR(Transrapid)系列磁悬浮列车是常导高速磁浮列车的代表。图1为车辆系统的模型图[13]。德国TR06列车的每节车厢有4个磁浮转向架,每个磁浮转向架由4个悬浮电磁铁和4个导向电磁铁组成,车厢和磁浮转向架之间采用空气弹簧连接。

图1 车辆系统模型
当以轨道梁为研究对象而不对磁浮车辆做具体研究时,可只考虑车辆和磁浮转向架的沉浮和点头运动,且假设车厢和磁浮转向架为刚体,其重心和几何中心重合,车辆竖向和横向是弱耦合。图1中,M和M分布表示车厢和磁浮转向架质量,J和J分为车厢和磁浮转向架的转动惯量,K和C分别为二系悬挂的刚度和阻尼。
以车厢和磁浮架的静平衡位移为坐标零点建立系统的动力方程,竖向运动坐标取向下为正,同时点头运动以逆时针方向为正,车厢和磁浮转向架的受力图如图2所示。
其中:


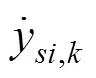
根据达朗贝尔原理,磁悬浮车辆系统的竖向动力学方程如下。
车厢的沉浮运动:

车厢的点头运动:

式中:l表示第节车厢的第个二系悬挂点到车体重心的距离。y为第个车厢的位移;α为第个车厢的点头角。
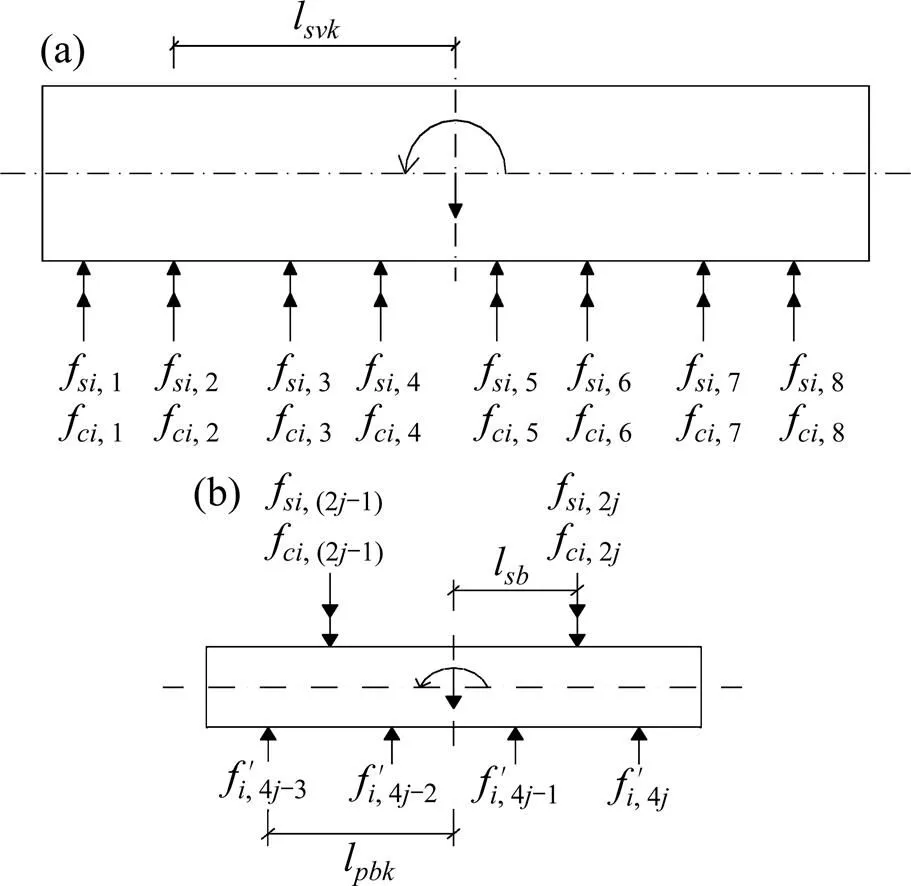
(a) 车厢;(b) 磁浮转向架
磁浮转向架的沉浮运动:
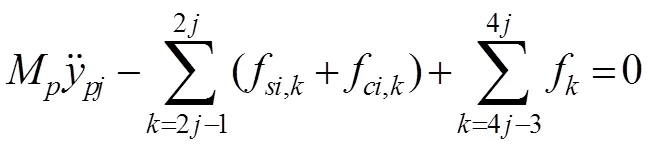
磁浮转向架的点头运动:

式中:l表示转向架上的二系悬挂点到转向架重心的水平距离;l表示第个均布悬浮电磁力合力作用点到磁浮转向架重心的水平距离;y为第个转向架的位移;β为第个磁浮转向架的点头角。
2 PID控制器模型
常导磁浮列车和轨道梁之间通过电磁吸引力实现悬浮。磁浮车辆上的电磁铁采用EMS-type SC magnets模型[14],恒流线圈产生恒定的电磁吸引力来平衡车辆自重,控制线圈产生控制电流并根据控制电压的变化而迅速变化,用来调节电磁吸引力稳定磁间隙。
利用安培环流定理和能量转换原理,电磁铁的吸引力可用式(7)表示:
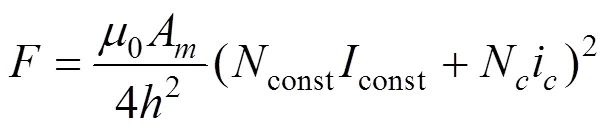
式中:const为恒定电流,用来平衡磁浮车辆自重;i为控制电流,调节悬浮间隙至额定间隙0。
根据基尔霍夫定律,整个电磁铁回路的电压可表示为
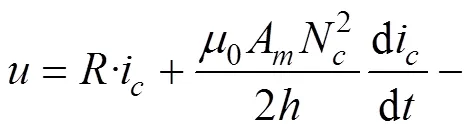
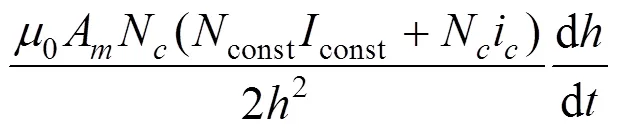
常导磁浮列车的磁浮间隙一般控制在8~12 mm。当车辆过桥时,车辆的振动会引起桥梁的振动,同时桥梁的振动又作为一种激励对车辆的振动产生影响,因此磁浮车辆和轨道梁之间的磁浮力一直处于动态变化中。而电磁铁系统是一个开环系统,故需引入控制器来维持车辆和轨道梁之间的磁浮间隙。当电磁铁上的传感器监测到车辆和桥梁之间的间隙发生变化时,控制系统依据控制算法的结果,产生与磁间隙扰动成一定关系的控制电压,使电磁铁中的控制电流发生变化,调整电磁吸引力,保证车轨间隙在容许范围内,使车辆能够顺利平稳地通过轨道。
为减小系统的稳定悬浮误差,本文在比例-微分(PD)控制器的基础上,加入积分控制律Ⅰ,构成比例−积分−微分(PID)控制器。PID控制器结构简单,易于实现,控制效果理想。系统在PID控制器的作用下,根据误差信号分别进行比例、积分与微分运算,3个运算量之和作为控制信号输出给被控对 象[15]。PID控制器是一种线性控制器,根据给定值0()与实际输出值()构成控制偏差()=()–0(),其数学方程可用式(9)表示:

式中:K为比例常数;T为积分时间常数;T为微分时间常数。
每个电磁铁单独调节其电磁力,保证每个电磁铁的磁间隙稳定在额定变化范围内。为得到使系统稳定的PID参数,先将磁浮车辆悬浮于轨道梁上,将车辆和轨道梁的动力响应作为干扰,以磁浮间隙是否能够收敛作为PID参数选取的依据。
3 轨道梁竖向振动的有限元模型
有限元法不仅计算精度高,而且对不同支座工况、不同材料以及变截面的梁都有较强的适用性,是目前应用最为广泛的一种离散化数值方法。相较于连续梁模型,采用有限元离散模型计算轨道梁动力响应时,只需将荷载工况简化为上桥、满载、离桥和完全离开4种工况,不必因车桥长度关系而细分其他工况。轨道梁的模型采用磁悬浮系统中广泛使用的简支梁模型。对于一维梁,忽略其轴向变形,仅考虑其平面内变形,即每个单元考虑两边的转角和位移4个自由度。
整个轨道梁的运动方程如式(10)所示:

式中:[],[]和[]为整体坐标下轨道梁的总质量矩阵、总刚度矩阵和阻尼矩阵;{}为轨道梁位移向量;{}为总荷载向量。
为提高计算效率,采用振型分解法将方程(10)解耦,得到方程(11):
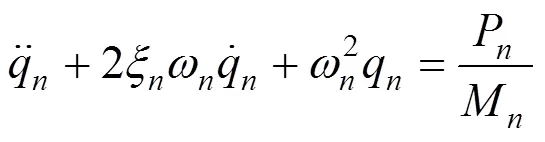
车轨系统与磁浮系统最大的区别在于车辆和轨道梁是否接触。磁浮系统的轨道梁承受的是电磁力作用。电磁铁模块产生电磁力后,需要转化为在电磁铁长度范围内的均布力,才能运用轨道梁计算公式(11)计算轨道梁的位移、速度和加速度。电磁力的转化分为2步[16]:首先要计算第个电磁铁模块在时刻的首端坐标x和尾端坐标x,其次要将电磁力f′在区间[x,x]内进行均匀化处理。
4 车桥竖向振动方程的耦合及求解
在求解车桥耦合振动时,本文以磁轨处为界,分别建立磁浮车辆和轨道梁2个子系统,磁浮车辆和轨道梁之间的耦合作用为非线性的电磁力,电磁力中的磁间隙由车辆和轨道梁之间的运动状态和初始磁间隙决定,电磁力中的电流由PID控制器控制和调节。整个磁浮车辆−轨道梁耦合作用的计算过程如下。
步骤1:计算t时刻每个电磁铁的首尾坐标和传感器的坐标;
步骤2:根据轨道梁和车辆的运动状态计算当前时刻每个电磁铁模块下的磁间隙状态。然后由控制算法式(9)得到当前控制电压,采用四阶龙格库塔法求解式(8)得到电磁铁模块的控制电流,并用式(7)求出当前时刻的电磁力;
步骤3:将步骤2中求得的电磁力作用于车辆系统,并将每个模块下的电磁力转化为均布力后作用于轨道梁系统,采用四阶龙格库塔法求解磁浮车辆动力学公式(3)~(6)以及轨道梁动力学公式(11),计算当前时刻磁浮车辆和轨道梁的动力响应;
步骤4:计算与安装在电磁铁上的传感器相对应的磁浮车辆和轨道梁的位移、速度和加速度,作为下一个采样时刻输入的磁浮间隙信号;
步骤5:判定车辆是否完全通过轨道梁,“是”则结束计算,“否”则循环执行上述步骤1~4。
5 算例分析
5.1 模型参数
采用Mathematica软件仿真模拟3节车厢编组的磁浮车通过8跨简支梁,每跨简支梁长24.768 m。磁浮列车运行速度设定为超高速磁浮研发项目提出的600 km/h,磁浮间隙稳定在8~12 mm为电磁力的控制条件,磁浮车辆的单位重量[16]约为25 kN/m。磁浮车辆参数以德国的TR06磁浮列车为依据,详见表1。磁浮轨道梁的设计以1>1.1/为依据,采用提出的与时速600 km超高速磁浮配套的预应力混凝土梁,轨道布置为单线形式,轨道梁截面形式见图3,耦合振动分析中所需的轨道梁参数见表2。

图3 轨道梁截面形式

表1 车辆系统模型参数

表2 轨道梁参数
5.2 模型验证
为验证提出的磁浮车桥竖向耦合振动理论分析方法的正确性及程序的可靠性,采用上海磁浮线进行仿真模拟,将磁浮车桥动力仿真值与2003年测试的上海磁浮线的实测数值进行对比。现场测试选取的为简支轨道梁,由于条件限制,现场测试最高车速为300 km/h,测试车辆为5节车厢。由于轨道梁刚度较大,车速又比较低,轨道梁跨中动位移较小,几种车速测试结果相差不大。文中选取了试验磁浮列车以300 km/h通过简支轨道梁时,梁跨中挠度实测时程图与理论计算时程图进行对比,对比结果如图4所示。
从图中可以看出,理论计算结果与实测的宏观特征是相似的,都可以看到轨道梁的振动经历了车辆上桥、满载、离桥和离开后轨道梁自由振动等特征。由此可认为提出的磁浮控制模型分析方法具有一定的参考意义。

图4 实测结果与理论计算对比
5.3 车桥耦合系统动力响应
通过仿真模拟车辆通过轨道梁的过程,得到磁浮车辆和轨道梁的动力响应规律。
5.3.1 电磁力和磁浮间隙
第19个电磁铁的电磁力和磁浮间隙时程如图5所示。显然,电磁力具有周期性,其值在自重附近上下波动,磁浮间隙在8~12 mm之间,满足要求,且磁间隙随着轨道梁挠度的变化而变化。当电磁铁运动到约跨中位置时,磁浮间隙值最小,在控制器调节下电磁力小于磁浮车辆的自重,磁浮间隙逐渐增加。当电磁铁运动到2根轨道梁的交点处附近时,磁浮间隙上下波动并出现最大值,电磁力变化剧烈,先迅速减小到34 kN,然后迅速增加到40 kN。因此,在磁浮间隙的控制中应限制轨道梁的转角,且注意轨道梁跨中和交界处的磁浮间隙控制。
5.3.2 磁浮车辆
第3个磁浮架和第1节车厢的加速度时程如图6所示。在评价车辆动力性能时,上海磁悬浮项目要求车辆竖向加速度限值[7]为0.4 m/s2。图6中,磁浮转向架的加速度最大值为1.2 m/s2,远大于规定的加速度。而车厢加速度值在0 m/s2上下波动,最大的加速度值为0.17 m/s2,远小于其限值,这充分说明如果不加二系悬挂系统而直接将电磁力作用在车厢上,难以满足车辆平稳性和舒适性的要求。车厢和悬浮架之间的空气弹簧起到了一个较好的隔振作用,有效减少磁浮列车过桥时车厢的振动作用,提高车辆的运行平稳性,保证旅客的乘坐舒 适性。

(a) 电磁力;(b) 磁浮间隙
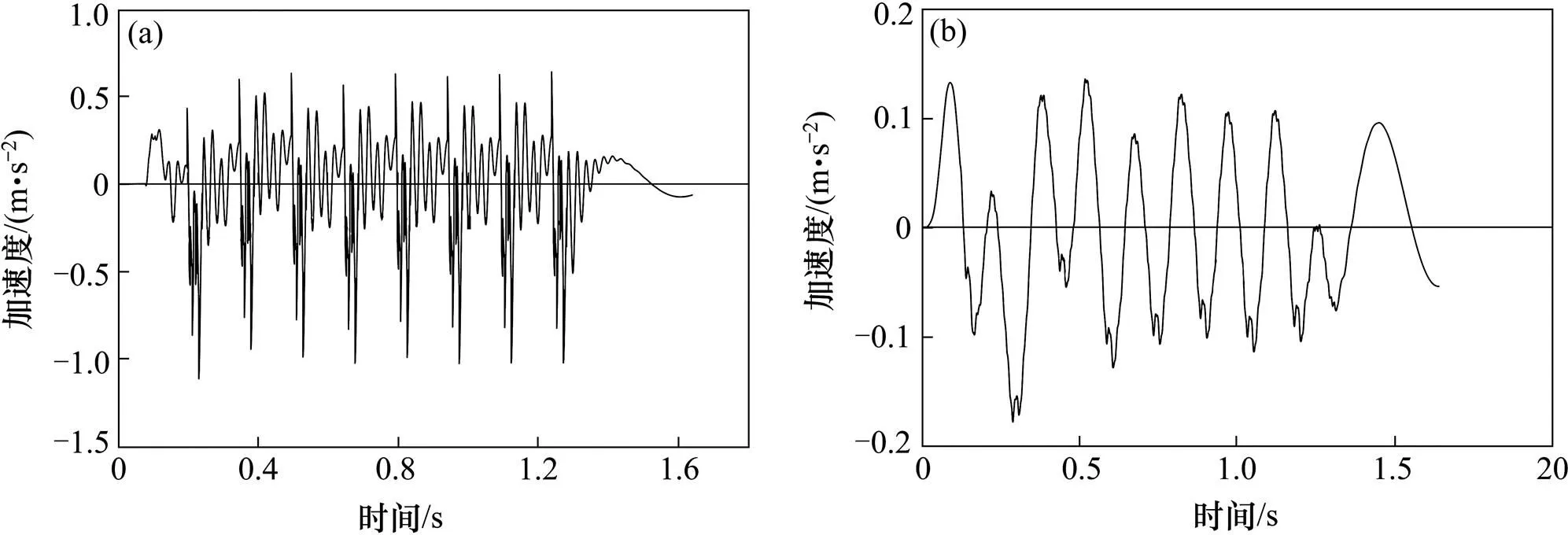
(a) 磁浮转向架;(b) 车厢
5.3.3 轨道梁
图7为轨道梁跨中的位移和加速度时程图。取其中的4跨轨道梁进行分析,图7(a)为第1,3,5和7跨轨道梁的跨中位移时程曲线,4跨轨道梁的变化类似,轨道梁跨中最大动位移约为1.30 mm,其跨中静位移为1.21 mm,动力放大系数为1.074,其竖向挠度主要由列车的重力荷载引起。简支梁的竖向刚度限值为/4 000(即6.192 mm),轨道梁跨中的最大位移值远小于轨道梁的竖向刚度限值。图7(b)为第3跨轨道梁跨中加速度时程图,轨道梁的加速度最大值为0.6 m/s2,跨中加速度最大值出现在车辆进入和离开轨道阶段,该结论与梁鑫等[17]研究结论一致。
5.4 不同参数下的仿真结果
为研究磁浮车辆运行速度对轨道梁振动的影响,探究不同速度下轨道梁跨中位移的变化规律,设置磁浮车辆速度从300~800 km/h变化,保持其他参数不变,建立仿真模型获得轨道梁跨中动力放大系数。如图8所示,当车辆运行速度不超过550 km/h时,动力放大系数对速度的变化不敏感,基本在1.01~1.04之间,而当运行速度大于550 km/h时,动力放大系数随速度的增加而迅速增大。600 km/h运行速度所对应的梁跨中动力放大系数为1.08,满足德国磁浮规范规定[18]竖向动力系数不超过1.4以及上海磁悬浮示范线的竖向动力放大系数不超过1.2的要求。
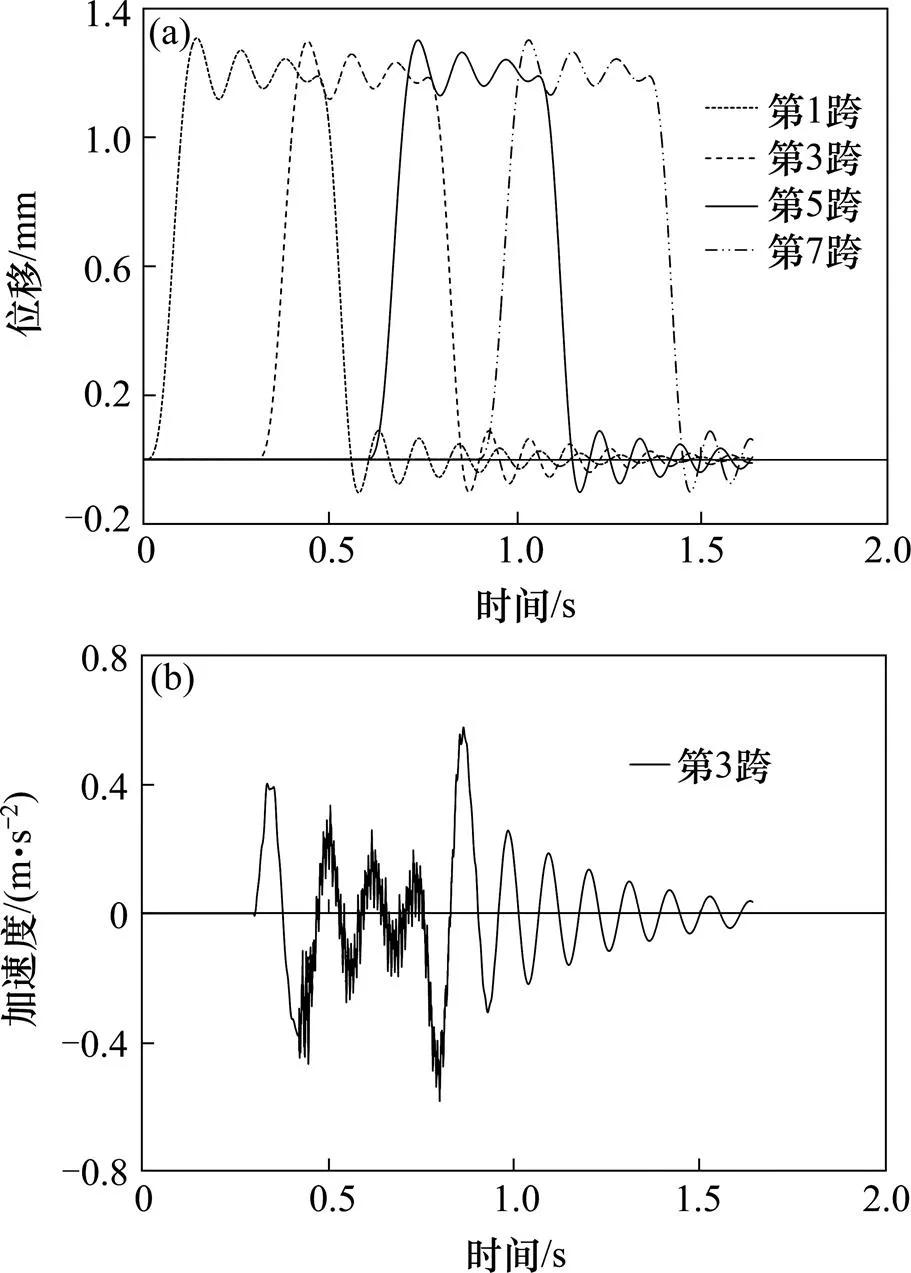
(a) 位移;(b) 加速度
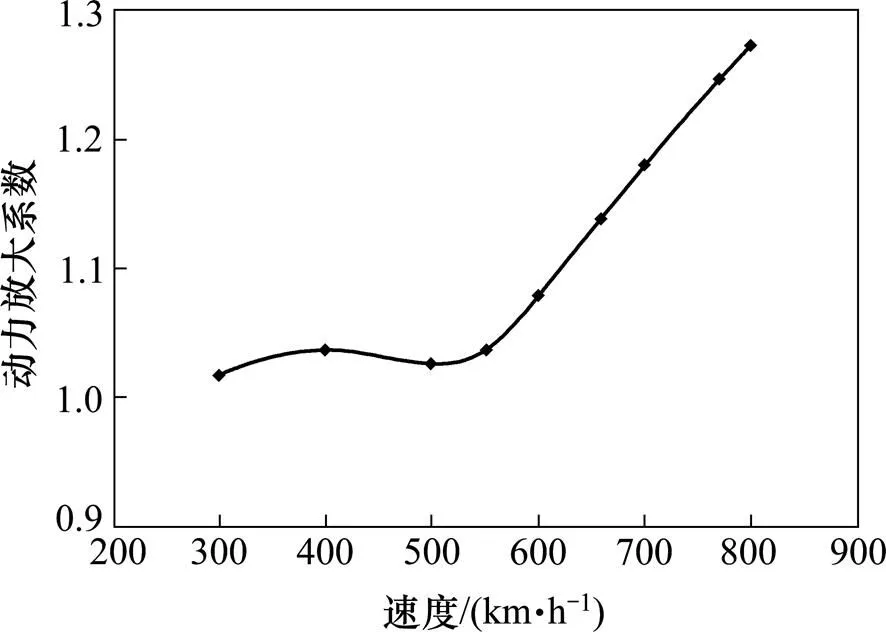
图8 不同速度下轨道梁跨中动力放大系数
以TR06列车总重量0为基础,仿真模拟总质量为0.9~1.50的磁浮车辆,得到磁浮车厢的加速度和轨道梁跨中位移的动力放大系数,结果如图9所示。图9(a)中,随着车体质量的增加,磁浮车厢加速度也随之增加,车厢加速度小于0.4 m/s2,满足车辆性能要求。图9(b)中,尽管轨道梁的跨中动力放大系数随着车体质量的增加而增大,但动力系数仍满足限制要求。

(a) 车厢加速度;(b) 轨道梁跨中动力放大系数
6 结论
1) 采用轨道梁和磁浮车辆分开建模,通过PID控制磁浮力实现车轨之间的振动耦合的分析方法,能完整反映出整个系统最本质的车轨主动电磁耦合关系,且有较高的计算效率。
2) 电磁力具有周期性,通过对电磁力的调节可以稳定磁浮间隙。磁浮间隙在轨道梁的交界和中点处分别出现最大和最小值。简支轨道梁支座处转角的不连续,导致了磁浮间隙的突变。在磁浮间隙的控制中,应注意轨道梁跨中和交界处的磁浮间隙控制。
3) 空气弹簧起到了较好的隔振作用,使得磁悬浮车厢加速度远小于磁浮转向架加速度,满足规定限值。
4) 与时速600 km高速磁浮配套的轨道结构的动力响应满足规范要求。轨道梁跨中加速度最大值出现在车辆进入和离开轨道阶段。
5) 通过改变车辆的运行速度以及质量,分析轨道梁和车厢的动力响应可知,轨道梁存在一个临界速度,在该速度之前轨道梁对速度的变化不敏感,超过该速度以后,轨道梁的动力放大系数会迅速增加。随着磁浮车辆质量的增加,轨道梁的竖向位移以及磁浮车厢的加速度都有所增加。
[1] 吴祥明. 磁浮列车[M]. 上海: 上海科学技术出版社, 2003. WU Xiangming. Maglev train[M]. Shanghai: Shanghai Scientific & Technical Press, 2003.
[2] 刘希军, 张昆仑. 中低速磁浮列车垂向动力学分析[J].铁道科学与工程学报, 2014, 11(1): 137−142. LIU Xijun, ZHANG Kunlun. Vertical dynamics analysis of middle and low speed maglev vehicle[J]. Journal of Railway Science and Engineering, 2014, 11(1): 137−142.
[3] 李小珍, 洪沁烨, 耿杰, 等. 中低速磁浮列车-轨道梁竖向耦合模型与验证[J]. 铁道工程学报, 2015, 32(9): 103−108. LI Xiaozhen, HONG Qinye, GENG Jie, et al. The medium and low speed maglev train-track beam coupling vibration model and verification[J]. Journal of Railway Engineering Society, 2015, 32(9): 103−108.
[4] 杨平, 刘德军, 李小珍. 中低速磁浮简支轨道梁动力系数研究[J]. 桥梁建设, 2016, 46(4): 79−84. YANG Ping, LIU Dejun, LI Xiaozhen. Investigation of dynamic factors of low and medium speed maglev simply-supported guideway beam[J]. Bridge Construction, 2016, 46(4): 79−84.
[5] 轨道交通装备关键技术产业化实施方案[J]. 中国战略新兴产业, 2018(5): 76−79. Implementation plan of industrialization of key technologies for rail transit equipment[J]. China Strategic Emerging Industry, 2018(5): 76−79.
[6] CAI Y, CHEN S S, Rote D M, et al. Vehicle/guideway interaction for high speed vehicles on a flexible guideway[J]. Journal of Sound and Vibration, 1994(5): 625−646.
[7] 时瑾, 魏庆朝, 吴范玉. 高速磁浮铁路轨道梁振动分析及控制研究[J]. 中国安全科学学报, 2003(10): 80−84. SHI Jin, WEI Qingchao, WU Fanyu. Study on vibration of the beam magnetic levitation express railway and its control[J]. China Safety Science Journal, 2003(10): 80−84.
[8] 詹旋裕. 高速磁悬浮中等跨度三跨刚构桥振动特性研究[D]. 上海: 上海交通大学, 2007. ZHAN Xuanyu. Vibration characters of middle length span rigid beam of high speed maglev transportation[D]. Shanghai: Shanghai Jiaotong University, 2007.
[9] 梁鑫, 马卫华. 2种磁轨关系的磁浮车桥相互作用比较分析[J]. 铁道科学与工程学报, 2017, 14(4): 845−851. LIANG Xin, MA Weihua. Comparative analysis of two kinds of magnet-track relationship of maglev vehicle and guideway interaction[J]. Journal of Railway Science and Engineering, 2017, 14(4): 845−851.
[10] SHI J, WANG Y J. Dynamic response analysis of single-span guideway caused by high speed maglev train[J]. Latin Am J Solids Struct, 2011, 8(4): 213−218.
[11] YAU J D. Vibration control of maglev vehicles traveling over a flexible guideway[J]. Journal of Sound and Vibration, 2008(321): 184−200.
[12] REN S B, Romeijn A, Klap K. Dynamic simulation of the maglev vehicle/guideway system[J]. Journal of Bridge Engineering, 2010, 15(3): 269−278.
[13] 赵春发, 翟婉明, 蔡成标. 磁浮车辆/高架桥垂向耦合动力学研究[J]. 铁道学报, 2001, 23(5): 27−33. ZHAO Chunfa, ZHAI Wanming, CAI Chengbiao. Maglev vehicle/elevated-beam guideway vertical coupling dynamics[J]. Journal of the China Railway Society, 2001, 23(5): 27−33.
[14] WANG S K. Levitation and guidance of a maglev vehicle using optimal preview control[D]. Pittsburgh: Carnegie Mellon University, 1995.
[15] 曹广忠, 潘剑飞, 黄苏丹, 等. 磁悬浮系统控制算法及实现[M]. 北京: 清华大学出版社, 2013. CAO Guangzhong, PAN Jianfei, HUANG Sudan, et al. Control algorithms and their realization in the magnetic levitation system[M]. Beijing: Tsinghua University Press, 2013.
[16] 滕延锋. 高速磁浮轨道梁在车辆荷载作用下的振动研究[D]. 上海: 上海交通大学, 2008. TENG Yanfeng. The study of vibration of high-speed maglev guideway interacting with vehicle[D]. Shanghai: Shanghai Jiaotong University, 2008.
[17] 梁鑫, 罗世辉, 马卫华. 基于相似原理的磁浮车桥耦合振动研究[J]. 铁道科学与工程学报, 2014, 11(3): 31−36. LIANG Xin, LUO Shihui, MA Weihua. Study on coupling vibration of maglev vehicle-bridge based on the similarity theory[J]. Journal of Railway Science and Engineering, 2014, 11(3): 31−36.
[18] 王理达. 中低速磁浮轨道梁关键技术研究[D]. 成都: 西南交通大学, 2014. WANG Lida. Research on key technology of low and medium speed maglev guideway girder[D]. Chengdu: Southwest Jiaotong University, 2014.
Vertical coupling vibration analysis of ultra high-speed maglev vehicle guideway
NI Ping, XU Chaochao, HE Jun, TENG Nianguan
(School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiaotong University, Shanghai 200240)
To analyze the vertical coupling vibration of ultra high-speed maglev vehicle guideway, an analysis method was developed based on finite element beam model and proportion-integration-differentiation (PID) controller-magnetic buoyancy model. To improve the computational efficiency of the method, the whole coupling system was divided into vehicle and guideway two subsystems at the place of magnetic buoyancy, and used magnetic buoyancy calculated by PID controller to accomplish the vibration coupling of maglev vehicle and guideway. The vibration response of each subsystem was calculated by the methods of the mode decomposition method and the four order Runge-Kutta method. To verify the effectiveness of the method and study the coupling vibration characteristics of the whole system, analyzing the vertical coupling vibration of the ultra high-speed maglev vehicle guideway system by using Mathematica software, obtaining the vibration response of guideway and maglev vehicle with the speed of 600 km/h. This research can provide a reference for the design and key technology research of the ultra high-speed maglev track structure.
maglev; ultra-high speed of 600 km/h; maglev vehicle guideway beam coupling vibration; magnetic buoyancy; PID-controller
U237
A
1672 − 7029(2019)06− 1361 − 08
10.19713/j.cnki.43−1423/u.2019.06.001
2018−08−16
国家重点研发计划项目(2016YFB1200602-28);上海市自然科学基金资助项目(16ZR1417300);
何军(1968−),男,河北唐山人,副教授,博士,从事结构振动和可靠性研究;E−mail:junhe@sjtu.edu.cn
(编辑 涂鹏)
