融合社会关系的机会网络有效数据转发策略*

严晔晴，陈志刚+，吴 嘉，王磊磊

1.中南大学 软件学院，长沙 410075

2.“移动医疗”教育部-中国移动联合实验室，长沙 410083

1 概述

机会网络是一种基于移动自组网[1]的延迟容忍网络。在机会网络中，由于节点的移动具有随机性，节点之间不存在端到端的稳定链路。在信息传递和数据转发时，节点将需要被发送的信息存储在自身缓存，再将信息转发给相遇节点。信息通过节点的运动不断地进行转发，直到目的节点接收到数据信息时转发过程结束。这种数据传输方式被称作“存储-携带-转发”机制，是机会网络中数据传递和路由选择的基本原则[2-3]。由于通信路径的不稳定性，传统的端到端的数据转发机制在机会网络中不再适用，怎样在机会网络中使用高效的路由算法成了目前面临的最大挑战[4]。

现今机会网络的应用场景越来越多，主要适用于没有固定基础设施的恶劣环境下的网络通信。由于贫富差距的存在，在偏远地区经常存在因网络基础设施不完善而不能接入互联网的情形，而使用机会网络技术能够提供非即时，但价格低廉、相对可用的网络服务。在不能覆盖无线信号的大范围区域内进行的野生动物追踪研究也是机会网络应用的一个重要领域。在现代社会使用车辆出行是一种普遍现象，随着配置无线智能设备的车辆不断增多，行驶在道路上的车辆也可以进行无线短距离通信，从而可以构成动态的、密度不均匀的、节点不定速移动的车载无线网络，这种车载无线网络也是机会网络的一个重要应用场景。

机会网络展示的是一种在不稳定状态下，通过节点移动带来的接触机会进行数据传输的移动自组织网络传播方式[5]，也是基于“存储-携带-转发”策略的数据转发模型。两种简单的路由选择算法在机会网络中开始普及使用。一种是Epidemic算法，是一种类似于疾病传播的数据转发机制，该算法中所有的节点简单地将信息传递给所有相遇节点，具有较高的消息传输成功率，但网络开销也较大。另一种是Direct Transmission算法，与Epidemic算法不同的是采用Direct Transmission算法时，节点只有在遇到目的节点时才传递信息，其余情况时不传递信息。和其他算法相比Direct Transmission算法网络开销非常小，但是传输成功率低。

然而，随着各种具有短距离通信功能的便携式移动设备的迅速普及，平板电脑、手机、车载感知设备等终端被人类在日常生活中所携带,且处于不断的运动之中。人们在社会生活中的活动不仅符合机会网络节点随机移动的特点[6]，而且出现了人类社会的某些社会特性。研究表明，节点间的社会关系对节点之间的相遇时间和持续时间具有重要的影响，可以提高网络的消息传输成功率，并减小路由开销[7]。然而，在这种应用场景内，普通的机会网络信息传输与数据转发机制不再占有优势，基于社区和社会性的机会网络算法更为适用和稳定。

本文研究了节点间的社会关系，提出了一种融合社区和社会性的机会网络有效数据转发策略（a transmission data forwarding strategy integrating social relationships in opportunistic networks，EFIS）。本文在一定时间周期内，对机会网络中的节点进行社区划分，利用网络的社会性对社团结构中的节点进行精简，缩小网络规模。实验结果证明本文提出的这种算法可以准确地减少网络中的低效或者无效节点，提高网络传输效率，减小资源消耗。

本文贡献如下：

（1）在机会网络中，提出一种融合社区和社会性的数据转发策略。将网络划分成社团之后，采用了一种方法来减少低效节点。

（2）在减少低效节点之后再次将社团结构进行收缩，以保持社团的紧密性和数据传递的高效性。

（3）在保证传输成功率的同时，减少了无效节点的耗能，降低了网络路由开销。

本文的结构划分如下：在第2章中，描述并分析了机会网络现有的研究成果和相关工作。在第3章中，提出了一种基于社区和社会性的数据转发方法。仿真实验的结果将在第4章给出。第5章对本文做的相关工作进行了总结。

2 相关工作

机会网络路由作为实现间歇式通信环境下节点通信的理论基础，具有十分重要的研究意义。基于“存储-携带-转发”的数据转发模式，现提出的多种数据转发方式和路由算法的目标均致力于减小数据转发造成的路由开销和提高数据传输成功率。在机会网络中，按照在数据转发时是否需要额外的辅助信息，可以将目前的机会网络路由算法分为直接型和辅助型。

直接型的机会网络路由算法可以分为扩散传播、被动等待、多拷贝三类。文献[8]提出了一种类似疾病传播的算法Epidemic算法。在Epidemic算法中，当两个节点相遇时，通过交换对方所缓存数据包的ID，判断对方节点具有哪些本节点所不具备的数据，并从对方节点获得这些数据，得到两个节点数据的一致。通过节点之间数据的两两交换，目的节点可以得到在它之前所有节点包含的信息。该算法在某些场景中具有很高的传输成功率，很小的传输延迟，但同时网络负载大，算法适应性和可扩展性差。

文献[9]提出了一种被动等待算法Direct Transmission，该算法是一种源节点直接等待的数据传播机制。在数据传输过程中，源节点在没有遇到目的节点之前一直将数据信息保存至自身缓存，直到遇到目的节点才进行转发。Direct Transmission在现有的算法中，具有最低的网络开销，但同样具有非常低的传输成功率。文献[10]提出了一种多拷贝的路由算法Spray and Wait算法。Spray and Wait算法将信息的转发分成两个步骤：在Spray过程中，源节点将要传递的数据信息拷贝N次，将这些数据副本传递给不同的相遇节点，然后进入Wait过程。在传输过程中，当前节点不停地将数据信息转发至相遇节点，直到目的节点接收到信息时算法才会停止。

辅助型的路由算法又根据在数据转发策略设计时辅助信息的来源，将现存的一些路由算法进一步划分为基于数据属性、历史接触记录、节点信息、节点社会地位四类。文献[11]提出了一种基于数据属性的机会网络路由策略。在多个数据进行传输时，数据具有多种优先级，使用优先级执行缓冲区管理可以改善机会网络路由的性能。该算法提出可以根据数据属性信息，给定一些数据的优先级。在数据转发时，节点比较缓存内所存储数据信息的优先级，按优先级高低顺序依次进行存储信息的转发。文献[12]利用节点的历史接触记录，提出了一种基于节点概率的路由算法PRoPHET。当两个节点相遇时，它们的接触概率增加，否则随着时间变长，接触概率变小。PRoPHET算法通过节点交互的历史记录计算转发概率并提出路由转发的可能路径，具有和Epidemic算法相差无几的传输成功率，但是具有更低的路由开销。

文献[13]提出了一种基于社团结构进行数据转发的标签策略算法Label算法。该算法利用了节点历史纪录中所属社团结构的信息为每个节点打上标签，表明其所在社区的信息。节点在数据转发过程中，只将消息传递给目的节点或者与目的节点相同标签的其他节点。该算法操作简便，但是传输时延大。文献[14]提出了一种基于社区的转发算法Bubble Rap。根据节点间交互信息的历史纪录可以得到节点的活跃度，该算法将所有节点按照活跃度进行排名，得到全局排名和在社区中的局部排名。在数据转发时，节点按照全局排名依次将数据转发给排名较高的节点，直到转发给与目的节点处于同一社区的节点；再按照局部排名，在社区中进行数据转发，直至目的节点收到数据信息。Bubble Rap算法采用单拷贝的策略，传输成功率较低，转发延迟高。

文献[15]提出了一种基于节点速度的移动机会网络路由算法。这种算法在保证平均速度的同时研究速度多样性对移动机会网络的影响。节点速度多样性意味着较长的平均通信时间，以及在持续的总通信时间内通信的数量较少。这种算法通过调整节点速度多样性可以提高网络节点对资源的利用率，减少网络开销。文献[16]提出了一种利用网络编码的数据转发策略。这种算法利用一些能发现节点相遇可能性、包工具和编码的机制，提高网络的吞吐量。该算法的主要目标是在资源有限的条件下增加发现最佳路径的可能性，通过精确的建模和评估方法提高路由算法的有效性。

本文提出了一种融合人社区和社会性的高效数据转发策略，将机会网络中的节点划分成若干个社区结构。社区划分之后根据社区结构中节点的特征删除一部分低效节点，并进行社团结构的再收缩。这种数据转发方式将社区结构进行了精简，利用了社区内部传输速度较快的特点，使数据转发过程快速和高效，且相对稳定和安全。

3 系统模型

3.1 社区划分策略

机会网络中，在一定时间范围内，网络中节点的分布具有社会性，可以被划分为不同的社区。本文周期性地对节点的连接状态进行统计，按一定的时间间隔动态地划分网络的结构。在实际网络中并不存在绝对的彼此独立的社团结构，网络由许多彼此重叠互相关联的社团构成[17]，并不能划分为若干个相互分离的社区。若可以在一个网络中缩减节点数量，减小网络规模，就能得到连接更为紧密的网络结构。

一个社团可以看作由多个相互连通的“小的全耦合网络”的集合，这些“全耦合网络”称为“派系”。在利用派系过滤算法进行社团划分的时候，只要找到网络中各部分最大的全耦合子图，就可以利用该子图来寻找派系的连通子图，从而根据派系划分将网络划分成许多个不重叠的社区。

定义1（全耦合网络可能的初始大小N）网络中可能存在的最大全耦合网络的大小N。

定义2（全耦合网络）若在一个网络中每个节点到其他任意节点都存在路径，则称这个网络为全耦合网络。

定义3（重叠矩阵）类似于邻接矩阵的结构，矩阵的每一列对应一个派系，对角线上的值对应相应派系的规模，非对角线上元素代表两个派系公共节点数。

已知网络G=(V,E)，其中V={V1,V2,…,Vn}为节点集，表示n个节点的集合；设置一个可能的全耦合网络的大小N。从某个节点Vi出发，找到所有包含节点Vi且大小为N的社团结构后，删除节点Vi及连接该节点的所有的边。在找到所有大小为N的派系后，令N=N-1，不断迭代直到N为2。至此，就找到了社团中所有的社团结构。本文使用10个节点图示说明基于派系过滤算法的社区划分，这里设置N值为4。

使用派系过滤算法时，通常采用从大到小、迭代回归的算法来寻找网络中的派系。若一个顶点v和派系K所有的顶点都邻接，则称顶点v为派系K的邻接顶点。若是派系的邻接顶点与此派系的其他邻接点不再邻接，则称此邻接节点为第一类邻接点；若是派系的邻接顶点与派系的其他邻接顶点有连接，则称此邻接顶点为第二类邻接顶点。

对于一个初始节点Vi，设置一个包含所有两两相连的节点的集合A和一个与A中所有节点都相连的节点的集合B。集合B包含第一类邻接节点和第二类邻接节点。对节点Vi进行遍历，初始集合A={Vi}，B=Neighbor[Vi]，从集合B中移出一个节点放置到集合A。检查B中现存的所有元素是否仍然与A中所有节点相连，并删除B中不再与A中所有节点均相连的节点。根据这种方式不断地进行节点移动与删除，以寻找网络中的所有派系。在这个过程中，若A的大小未达到N之前B已经为空，或A、B为一个之前遍历时就已经存在的派系的子集，则停止计算返回递归第一步，再寻找下一个初始节点进行迭代遍历。反之，就得到一个新的派系，记录该派系，然后返回递归第一步继续寻找新的派系。本文采用如图1所示的10节点网络，图示说明派系划分的过程。

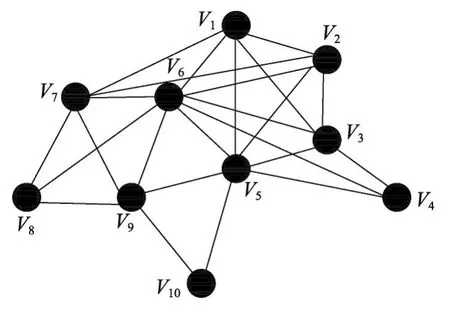
Fig.1 10-node network图1 某10节点网络结构

在这个10节点的网络结构中，目标是将网络划分为派系为4的社团结构。则假设初始节点V1，此时的集合B=Neighbor[V1]={V2,V3,V5,V6,V7}；若将节点V2移入集合A，集合B={V3,V5,V6,V7}，此时V3、V5、V6、V7与V1、V2均相连，不删除任何节点；再将节点V3移入集合A，集合B中仍然与A中节点均连接的节点只剩下V5、V6。因为集合A的大小未达到N且集合B不为空，故仍然可以进行遍历迭代。在遍历节点V2时，存在一个与遍历V1时相同的派系或派系的子集，此时该派系不保存。

找到了所有大小为设定全耦合网络大小4的派系后，将设定的初始派系大小N减1，再次进行派系的迭代寻找，直至N为2时停止。这样就得到了网络中的所有全耦合网络。

利用迭代回归的思想，对网络中所有节点进行遍历，得到该网络的6个派系如图2所示。

Fig.2 Result of clique partition图2 派系划分结果

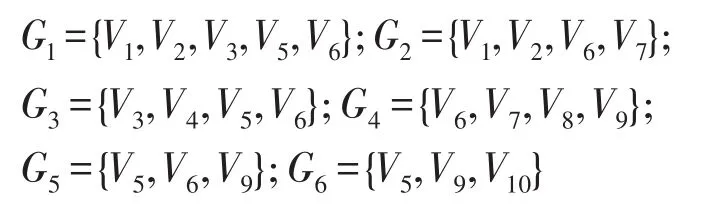
在找到网络中这些所有的派系后，可以得到这些派系的重叠矩阵。其中，矩阵的每一列对应一个派系，对角线上的值对应相应派系大小，非对角线上元素代表两个派系的公共节点数，如式（1）所示。

将派系重叠矩阵中对角线上小于N，而非对角线上小于N-1的元素置为0，其他元素置为1，就可以得到N派系社团结构的邻接矩阵式（2）。在这个矩阵中，各个连通部分代表各个N派系的社团。

根据式（2）的连通性分析，得到该网络的两个派系社团结构如图3所示。

Fig.3 Result of community partition图3 网络中的社团划分结果

在网络结构中，采用如上的社区划分策略可以将网络划分为若干个社团结构。

3.2 社团结构收缩策略

机会网络是一种不存在端到端连接路径的间歇性通信网络，但由于节点的移动，可以带来一定时间内相对稳定的通信机会。机会路由算法在进行信息传输与数据转发时，最重要的原则是寻找到能够将目标信息传达到目标节点的最佳路径。在能够保证最佳传输效率时，机会网络作为一种特殊延迟容忍网络，可以容忍适当的传输时延和消息丢弃。

由于机会网络的信息传播依赖于节点的运动，不同重要程度的节点对网络中信息流的影响大不相同，因此衡量节点的重要程度显得尤为重要[18]。若不对节点重要程度进行衡量，因为节点数目过多可能造成网络拥塞，将大大降低传输成功率且造成无法容忍的时延。

在将网络划分为若干个社团之后，机会网络中的节点从分散的节点结合成一个个的社团结构，但在社团结构中，各个节点的重要程度也有所差异。为了缩减社团结构，可以计算每个节点删除后网络效率的变化来衡量节点在社团结构中的重要程度。

对于具有S个节点的连通网络，dij(i,j=1,2,…,S)表示网络中节点Vi到节点Vj的最短距离，网络的平均距离表示为：

但若网络为非连通网络，网络的平均距离会成为无穷大。在这里引用网络效率来衡量节点重要性，网络的网络效率表示为：

dii=0，在一个社团结构中，若是删除节点Vi后，网络效率相对之前明显发生变化，则说明网络因为该节点产生了较大变化。在这里设置一个阈值衡量这个变化是否在可控范围内，若删除节点之后网络效率Kc变大且删除节点Vi前后Kc值差的绝对值大于阈值T，则直接从社团网络中删除该节点。

删除重要性不高的节点之后，社团结构较之前发生变化，此时再次对社团结构进行收缩以缩减网络规模。节点的凝聚度是衡量网络结构是否可以收缩的重要指标，表示为：

由式（5）和式（6），凝聚度φ[G]可以表示为：

其中,S≥2,D表示一个网络结构中所有节点的距离合积，当网络中只有一个节点时，φ[G]=1。G×Vi表示将节点Vi收缩得到的图结构，根据凝聚度可以算出节点在网络中的重要程度：

由式（7）和式（8）可以得出：

其中,ki表示与节点Vi的邻接节点的个数。计算出每个节点进行收缩后的重要度IM(vi)，若是进行收缩后的节点重要度IM(vi)大于控制参数ε，则用一个新的节点代替原本的节点及其所连的节点[19]。通过对社团结构中节点的属性进行分析，可以对社团结构的大小进行缩减，将社团结构进一步收缩，提高信息传播和数据转发的效率，伪代码如下：

算法1结构收缩策略

输入：子图Gn。

输出：缩减后的子图Gn′。

3.3 基于社会性的数据转发策略

节点收缩之后，网络规模减小，网络结构中的节点的社会性较强，在进行信息传播和数据转发时，通过社区进行转发。对于网络结构中的N个社团结构，通过对社会性的度量决定节点的转发方式。

社会性定义为节点通过网络到达其他节点的难易程度。社团结构的社会性定义为其社团中所有节点的社会性的平均值。

起始节点在信息传播与数据转发时，将所携带的数据复制若干份，发送给本节点的所有邻接节点，若邻接节点处于某社团结构，则将数据转发至自身所在的社团结构，否则传播给自己的所有邻接节点。

社区之间进行传播时，计算每个社区的社会性，已经得到数据副本的社团结构对自己能够到达的所有社区进行社会性的比较，将数据副本转发至社会性比自身社会性要高的副本。目的节点得到数据副本时，转发结束，发送反馈信息至起始节点。伪代码如下：

算法2数据转发机制

输入：缩减后的子图Gn′。

输出：传输路径。

3.4 算法优势及复杂度分析

当人类活动对网络结构产生影响时，移动节点的行为显示出某些社会特性。越来越多的用户利用具有短距离通信的便携设备相互联系和共享数据。在对机会网络的最新研究中，上下文信息、节点兴趣和节点社会属性经常被用作指标来度量机会网络路由的性能。在机会社会网络中，最大的问题是当大量的信息需要被转发时，传输延迟和路由开销极大。这是因为人们在数据传输过程中使用移动设备，而且周围没有合适的节点可以及时响应，最终导致传输延迟。许多现有的算法根据单个节点的社会特征进行路由选择，并没有考虑到机会网络中的节点聚集现象与人类生活中的社区非常相似，利用社区的概念可以减少大量的传输延迟和路由开销。

为了解决这些问题，该研究提出了一种融合社区和社会性的机会网络有效数据转发策略（EFIS）。由于单个节点的负载能力是有限的。本文采用基于社区的信息传输策略，因为通过社区进行的信息传输与数据转发具有稳定、高效且安全的特点，可以优化机会网络中的信息传递。

在本文算法中，采用派系的概念进行社区的划分，解决了真实社会场景中的重叠社区问题。由于在社区划分时单纯地使用历史社会连接属性，会造成社区内的节点重要程度差距迥异，故提出了一种社区结构缩减的策略。对复杂网络中多项节点重要程度指标进行了分析后，结合机会网络负载能力较差，节点移动带来的信息较少及传输不稳定等特征，本文采用了网络效率这一指标进行低效节点的删减，并使用节点凝聚度的概念对社区结构进行了再收缩。实验证明这种社团缩减方式可以有效收缩社区结构，使社区结构紧密。

在这个算法中，EFIS算法的时间复杂度是O(n)。信息通过社区结构进行传输，算法具有较高的传输速度及较高的传输效率。在Spray and Wait算法中，节点不断地复制数据并将数据分配给它的邻居，时间复杂度是O(n2)，PRoPHET算法的时间复杂度也是O(n2)。SCR（effective social relationship measurement and cluster based routing in mobile opportunistic networks）算法中节点通过社会关系进行选择，形成一个本地聚类，算法复杂度为O(n)，但是与EFIS算法相比路由开销较大。

4 仿真实验与结果分析

4.1 仿真场景及算法参数

本文使用ONE[20]仿真模拟环境模拟持有移动通信设备的行人在真实城市步行的场景,实现EFIS算法的仿真并与Spray and Wait算法、ProPHET算法和SCR算法进行性能比较。仿真场景的参数具体设置如表1所示，EFIS算法模型参数的设定如表2所示。

本文比较了相同场景下不同的路由算法的性能与表现并且分析了参数对EFIS算法的影响。在本文中，将EFIS算法与Spray and Wait算法[10]、PRoPHET算法[12]以及SCR算法[21]进行了比较。前两种算法是机会网络路由研究中两种经典的算法，SCR算法是一种最新的算法，其基于社会关系进行集群路由的选择。选用传输成功率、传输延迟、路由开销[22]三个性能指标对算法进行性能分析。通过实验表明，当N=14，t=0.15，ε=0.43时，EFIS算法性能综合最优。

Table 1 Simulation settings表1 仿真场景设置

Table 2 Parameter settings of algorithm表2 算法参数设置

4.2 实验结果分析

4.2.1 社区划分周期对消息传输成功率的影响

在社会联系较为紧密的机会网络中，应该采用融合社区和社会性的路由转发策略，社区划分周期对路由算法的影响十分重要。在一个周期内，可以认为网络中的节点状态和社区结构不发生改变，可以稳定地进行数据传播。如图4所示，当选取的社区划分周期较小时，由于社区结构不够稳定，造成社区划分对路由算法的指导效果不佳，传输成功率较低。随着划分周期增大，数据传输效率相应地提高。周期选取为900 s时，取得最佳传输成功率84%。随着划分周期继续增大，传输成功率下降，2 700 s时，传输成功率是72%，算法性能较900 s时要差。这是因为社区划分周期过长时，与实际情况不符。真实的节点分布状态与假定的稳定状态不一致，之前的社区划分结果不能很好地表示最新的社区结构。

Fig.4 Influence of community partition cycle on packet delivery rate图4 社区划分周期对消息传输成功率的影响

4.2.2 节点缓存和节点数目对路由算法的影响

在进行仿真实验时，将EFIS算法的性能与两种传统算法及一种最新算法进行比较。其中PRoPHET算法是基于概率的算法，Spray and Wait算法是基于多拷贝的算法，SCR是基于社会关系的聚集算法。

Spray and Wait算法、PRoPHET算法、SCR算法和EFIS算法在不同节点缓存大小和节点数目下对传输成功率的影响如图5所示。在节点缓存较小，节点数目较少时，存在消息丢弃，路由算法的传输成功率较低。随着节点缓存增大，节点数目增多，传输成功率相应提高。EFIS算法通过网络中的社会性，将网络中的节点划分成社团，对社团结构进行精简，去除低效节点后再进行数据转发。相对于Spray and Wait算法被动等待的特征，PRoPHET算法利用传输概率选择性复制并转发的策略，EFIS算法的传输成功率要更高。SCR算法是基于社会关系的算法，但是SCR算法中的本地聚类过程需要时间，在只能维持一段时间稳定性的机会网络中，消息传输成功率较EFIS算法差。

在Spray and Wait算法、PRoPHET算法、SCR算法和EFIS算法中，节点缓存和节点数目对于消息传输延迟的影响如图6所示。随着节点缓存增大，节点数目增多，算法的传输延迟增大。PRoPHET算法基于传输概率，在节点数目较多时需要进行大量运算，传输延迟最大。Spray and Wait算法进行多拷贝后，被动等待目的节点接收到消息，传输延迟也较大。SCR算法由于需要进行聚集过程，前期时延较大，随着节点缓存变大，节点数目增多，传输时延较为改善，但仍然比EFIS算法要大。综上所述，EFIS算法较其他三种算法传输时延较小。

Fig.5 Packet delivery ratio图5 消息传输成功率

Fig.6 Transmission delay图6 消息传输时延

Fig.7 Routing overhead图7 路由开销

在Spray and Wait算法、PRoPHET算法、SCR算法和EFIS算法中，节点缓存、节点数目对路由开销的影响如图7所示。Spray and Wait算法基于多拷贝，被动等待目的节点，路由开销相对稳定且较小。PRoPHET和EFIS算法随着节点缓存增大，节点数目增多，路由开销呈变小的趋势。由于EFIS算法在社区划分后，需要对结构进行收缩需要一定的路由开销，但与PROPHET算法需要不断地计算传输效率相比较，路由开销相对较小。SCR算法不仅需要分析节点的社会属性，而且需要进行集聚，路由开销较EFIS算法大。因此，相对其他三种算法，EFIS算法在具有社会联系的机会网络中路由开销最小。

5 总结与展望

在机会网络中，采用“存储-携带-转发”进行数据信息的转发。随着大量具有短距离通信功能的移动设备的出现，机会网络呈现了非常强的社会性，节点间的社会关系对节点之间消息传播具有重要影响，这些影响可以提高网络的消息传输成功率，并减小路由开销。在这种应用场景内，普通的机会网络信息传输与数据转发机制不再占有优势。

本文提出了一种融合社区和社会性的机会网络数据转发策略，通过派系过滤的思想对网络中的节点进行社团划分，根据节点对于网络的影响判断节点的重要性，删除低效节点，并对社团再次进行结构收缩。通过社会性，EFIS算法将数据转发至社会性较高的节点和社区，具有较高的传输成功率和较低的传输延迟。

在未来的工作中，将根据更多的社交行为来改进本文的数据转发算法，并研究机会社会路由中的安全性和隐私性。