改进K-Means算法在油水界面测量中的应用

宋安玲，任喜伟，姚 斌，何立风

(1.西安交通大学城市学院，陕西西安，710018；2.陕西科技大学电气与信息工程学院，陕西西安 710021)

0 引言

在油田联合站原油储罐中，由于流体的分异调整作用，石油占据油罐的高部位，水体则位于油罐的底部，石油与水体之间的接触面，称为油水界面。为了准确获取油水界面位置，需要借助某种油水界面测量装置对原油储罐内油水介质进行测量[1-3]，如图1所示。目前，多数油水界面测量装置内部呈现矩阵式分布的传感探极结构，物位传感器通过与油罐内介质接触获取油水界面数据，油水界面数据一般表现为有明显聚类特征的线性数据[4]。

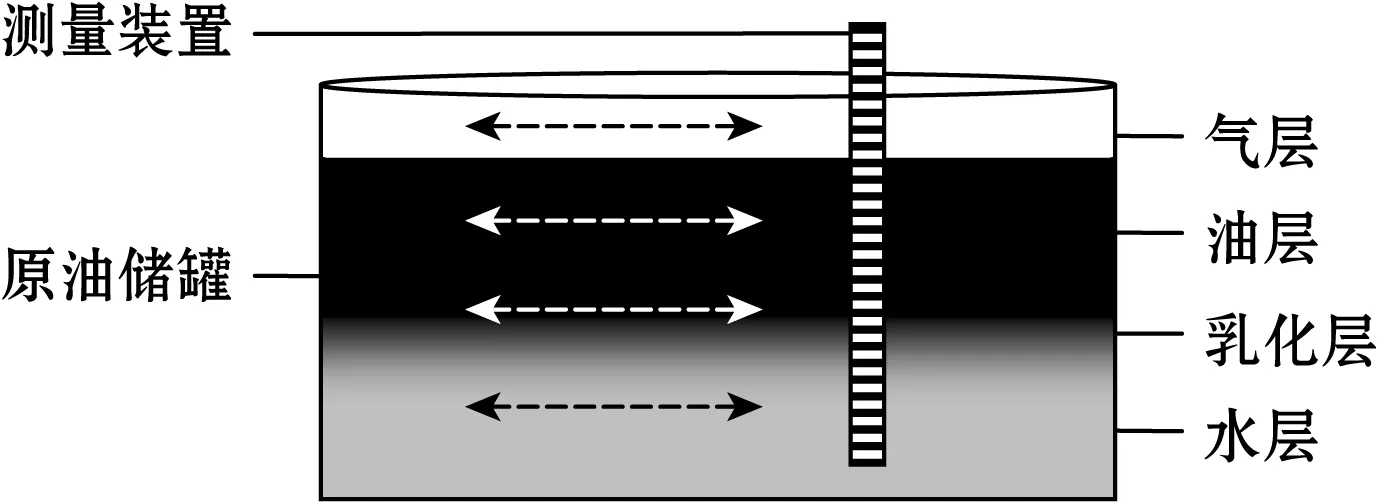
图1 原油储罐油水界面测量示意图

对油水界面数据进行分析、统计时，通常需要采取某种油水界面测量计算方法，才能获得油水界面位置及介质液位高度等结果。然而，油水界面传统计算方法在计算油水界面及液位高度时，完全依赖人工选取油水界面数据典型值。即，如果人工所选典型值在合理范围内，则油水界面及液位高度计算结果准确，否则，计算结果误差较大[5]。

1967年，MacQueen提出了K-means算法，很多学者对该算法进行了深入研究，因其易于描述和实现，且具有高效处理大规模数据的优点[6-9]，该算法已经被广泛应用到自然语言处理、医学、土壤和石油等众多领域[10-15]。张宜浩等将改进的K-means算法用于汉语词语归纳，提出用同义词词林中词的分类编号来降低特征维度[10]；刘海峰等将优化的K-means算法用于文本特征选择，通过优化初始类中心的选择模式及对孤立点的剔除改善了文本特征聚类的效果[11]；董侠等将K-means算法用于脑部医学图像研究[12]；郝智慧等将K-means算法用于分割含有噪声及灰度非同质的医学图像[13]；代希君等利用K-means算法为大样本光谱数据建立大尺度区域的盐分等土壤属性预测模型提供一种新的思路和方法[14]。刘远红等将K-means算法直接应用于油水界面检测，获得较好的计算结果[15]。鉴于K-means算法的优点和应用价值，本文针对原油储罐内油水界面数据具有数据规模较大、聚类特征明显和数据易于优化等特点，将K-means算法应用于油水界面测量计算过程中，提出基于K-means的油水界面测量聚类算法，通过算法改进，提高油水界面测量计算结果精度。

1 油水界面数据

本文以开发陕北延长油田某采油厂油水界面监控系统为例，说明测量过程及其油水界面数据。油水界面监测系统整体框架如图2所示。

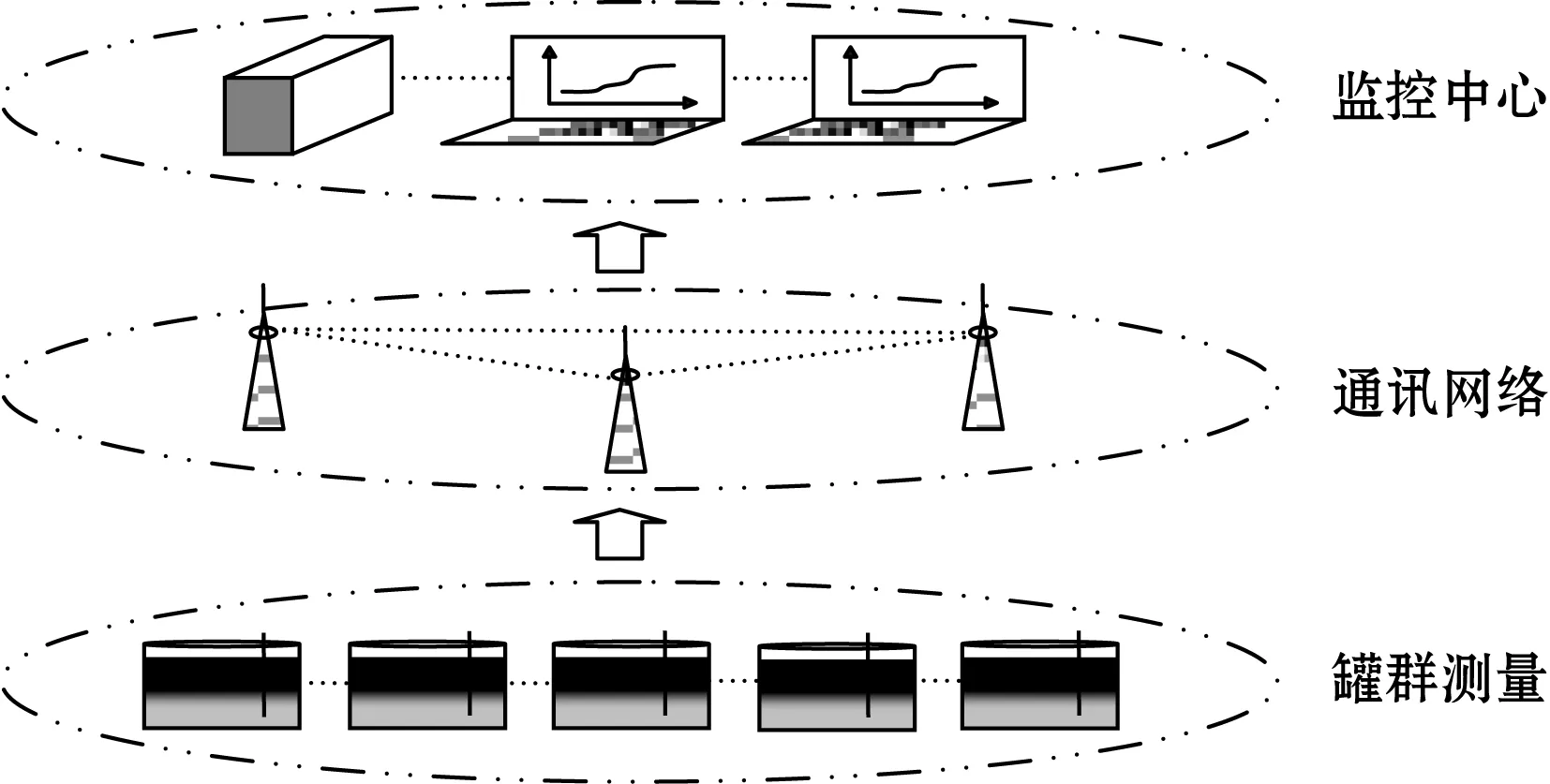
图2 油水界面检测系统整体框架

原油储罐中含有气层、油层、乳化层和水层。油水界面测量装置被安装在原油储罐中，采用矩阵式分布的传感探极结构，并与介质或罐壁之间构成N个层面检测横断面；在CPU的控制下，根据被测介质介电常数的不同，电磁微波式测量装置感应获得不同强弱的回波信号，经过信号过滤、解调、模数转换变为数字信号，生成油水界面数据；油水界面数据通过通信网络，上传给监控中心保存、统计、计算和展示数据，最终获得油水界面液位高度、体积、含水率等相关信息。

采油厂某原油储罐高为12 m，直径为12 m，测量装置上分布了100个接收传感器，传感器间距10 cm。测量装置工作后，可得到如图3所示的油水界面数据曲线图。从数据分析可知，原油储罐内宏观上处于同一层面的介质，其油水界面数据表征基本相近，有利于辨别原油储罐内不同介质，计算油水界面及液位高度。

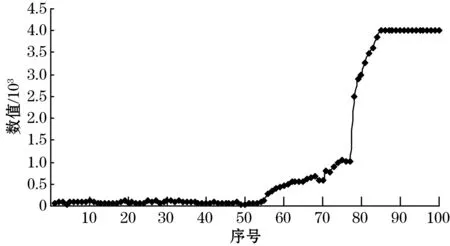
图3 油水界面数据曲线图

2 K-means算法

2.1 K-means算法描述

K-means算法是基于数据划分的无监督聚类算法，是典型的基于原型的目标函数聚类方法的代表，它是数据点到原型的某种距离作为优化的目标函数，利用函数求极值的方法得到迭代运算的调整规则。K-means算法以欧式距离作为相似度测度，在评价指标J最小时，求对应某一初始聚类中心向量的最优分类。J的数学表达如下：

(1)

式中：xi(i=1，2，3，…，N)为第i个二维向量样板元素，即被分类对象；uj(j=1，2，3，…，K)为第Sj(j=1，2，3，…，K)类的质心，K≤N；Sj为xi所属的第j个类别；rij为数据点xi被归类到Sj的时候为1，否则为0。

K-means算法的基本思想如下：

(1)从N个样本xi中选择K个对象uj作为初始聚类质心；

(2)根据欧氏距离计算方法对xi进行第一次分类，得到K个聚类Sj；

(3)计算每个聚类对象Sj的均值，作为新的聚类质心uj，并根据欧式距离计算每个对象xi与每个新质心uj的距离，对xi重新划分，重新得到Sj；

(4)重复步骤(3)，直到式(1)中J值最小，新质心uj不发生改变为止，即K-means算法收敛。

(5)统计K个聚类Sj数据个数，根据物位传感器间距，计算油罐内各层介质高度，获得油水界面。

2.2 K-means算法应用

按照上述油水界面K-means聚类算法基本描述，对图3油水界面数据进行计算。分别取4个数据u1=50、u2=334、u3=793、u4=2 506作为初始聚类质心，也可选取u1=238、u2=630、u3=793、u4=3 255作为初始聚类质心。区别在于2组数据聚类质心的变化，如表1所示，数据1需要进行3次聚类质心变化，可确定聚类质心为u1=81、u2=535、u3=932、u4=3 762，而数据2则需要进行5次聚类质心变化，才能确定。

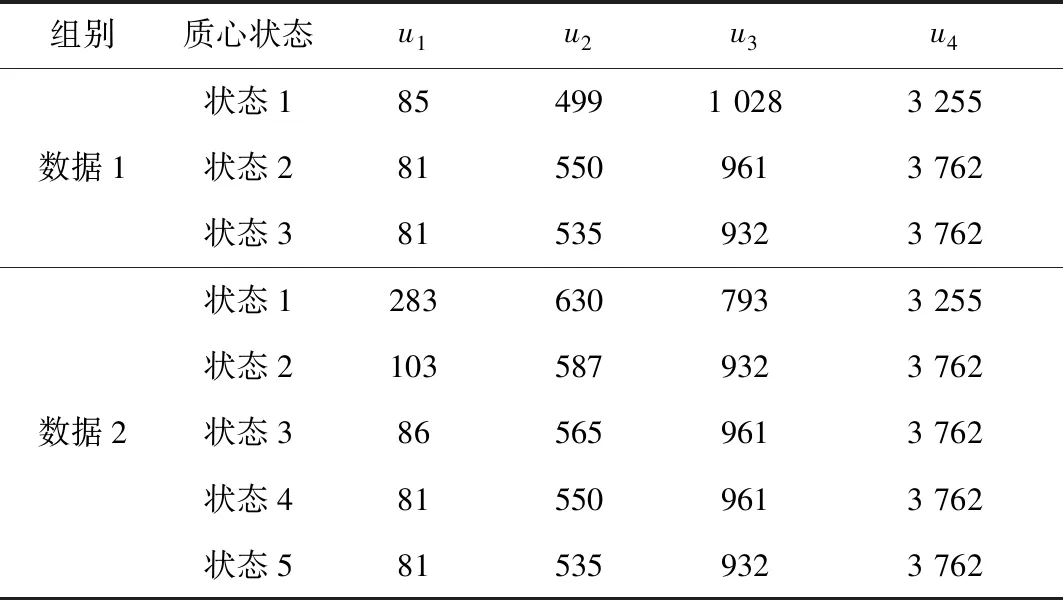
表1 K-means算法聚类质心变化过程

进一步确定数据集合S1、S2、S3、S4分别为{x1，x2，x3,… ，x56}、{x57，x58，x59,… ，x70}、{x71，x72，x73,… ，x77}、{x78，x79，x80,… ，x100}，统计得到m1=56、m2=14、m3=7、m4=23，计算得到H1=5.6 m、H2=1.4 m、H3=0.7 m、H4=2.3 m，计算结果与油水液位实际测量结果一致，K-means算法应用于油水界面测量的准确率得到验证。

2.3 K-means算法应用分析

在测量过程中因测量装置与原油储罐形状之间存在的某种客观因素，或是测量装置传感器本身存在的某种主观因素导致油水界面数据中存在错误数据，称之为伪数据。伪数据具体表现在油水界面数据存在前一个数据表征第一种介质特性，后一个数据表示第二种介质特性，而第三个数据又表示第一种介质特性的可能性，完全不符合原油储罐内介质数据的分布规律，这种情况被认为油水界面数据xi中存在伪数据。如图4所示的xi曲线分布，就是一组存在伪数据的界面数据，其中11号数据为1115，88号数据为50、91号数据为50，均属于伪数据。如果直接应用K-means聚类算法进行油水界面计算，计算结果为H1=5.7 m、H2=1.5 m、H3=0.7 m、H4=2.1 m，计算结果与实际不符。因此，需要对油水界面数据进行预处理，先消除伪数据，再进行聚类划分和计算。

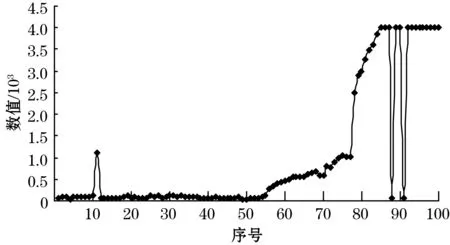
图4 包含伪数据的油水界面数据曲线图

3 改进K-means算法

3.1 改进K-means算法描述

针对油水界面存在伪数据的问题，本文提出改进K-means算法——中值预处理K-means算法计算油水界面，该算法结合中值过滤算法和K-means聚类算法的设计思想，一方面可对油水界面数据进行去伪预处理，另一方面可对油水界面数据进行合理聚类划分。改进K-means算法的基本思想如下。

(1)按照如图5所示的中值预处理模板遍历向量样本油水界面数据xi，获得一组新的向量样本。模板数据满足xj≤xj+1≤xj+2≤…≤xj+d/2≤…≤xj+d，其中，d为模板中数据个数(取值应小于油水界面数据介质临界处数据个数)，xj+d/2为模板中间位置取值。进行模板运算时，始终将模板内数据xj+d/2赋给模板起始位置所在变量，以此类推，直至N个油水界面数据xi遍历完毕为止，即获得一组新的向量样本。

图5 中值模板遍历油水界面数据示意图

(2)对中值预处理过的向量样本油水界面数据xi，选取4个数据值u1、u2、u3、u4分别作为气层、油层、乳化层和水层初始聚类质心；

(3)按照式(2)，分别统计油水界面各层介质聚类集合，即气层、油层、乳化层和水层对应的聚类集合S1、S2、S3、S4；

Sj={x∈xix=arg min‖x-uj‖2}

(2)

(4)按照式(3)对S1、S2、S3、S44组聚类集合求取平均值，作为油水界面新的聚类质心。其中，mj为每个聚类集合Sj的数据个数。

(3)

(5)递归(2)、(3)步，直至u1、u2、u3、u4数值不发生改变为止；

(6)统计最终确定的聚类集合S1、S2、S3、S4，统计m1、m2、m3、m4，并按照式(4)计算油水界面各层介质高度H1、H2、H3、H4。

Hj=hmj

(4)

改进K-means算法伪代码如下列程序所示。其中，dataArr为获取xi的数组，GetOWData()为获取xi的函数，dataMod为模板数组，sort()为排序函数，select()为获取有序数组中间值函数。模板长度为d，u为聚类质心数组，min()为判断(dataArr[i] - u[j])是否最小函数，dataS为记录聚类数组，n为统计聚类内数据个数数组，aveData为求聚类平均值函数，isConver()为判断u是否收敛的函数。

∥改进K-means算法伪代码

dataArr←GetOWData()

for i←1 to i <= N do

| for j←1 to j <= d do

‖ dataMod[j]←dataArr[i++ j]

‖ j←j++ 1

| end of for

| dataMod←sort(dataArr)

| mid←select(dataMod)

| dataArr[i]←mid

| i←i++ 1

end of for

for i←1 to i <= N do

| for j←1 to j <= K do

‖ if min(dataArr[i] ，u[j])

||| dataS[i]←dataArr[i]

||| n[j]←n[j]++ 1

‖ end of if

‖j←j++ 1

| end of for

| i←i++ 1

end of for

for j←1 to j <= K do

| for i←1 to i <= N do

‖ aveData[i]←aveData[i]++dataS[i]

‖ i←i++ 1

| end of for

| u[j]←aveData[i] / n[j]

| if isConver(u[j])

‖ return u[j]

| else

‖ return Kmeans()

| end of if

| j←j++ 1

end of for

3.2 改进K-means算法应用

针对图4所示存在伪数据的油水界面数据，采用改进K-means算法计算油水界及液位高度。首先进行中值预处理优化伪数据，根据油水界面数据介质临界区域数据个数大小，选择模板d取值为5，遍历整个油水界面数据，得到如图6所示的油水界面数据。其中11号数据由原来的1 115优化为115，88号、91号数据由原来的50优化为3 996。预处理后的油水界面数据反映了实际油罐内介质的特性，且数据整体趋于平滑，有利于各层介质聚类划分。

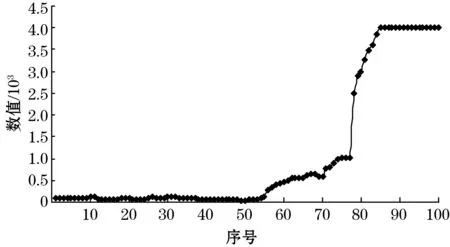
图6 中值预处理后的油水界面数据曲线图

之后分别取4个数据u1=85、u2=499、u3=1 028、u4=3 255为初始聚类质心，也可选取u1=238、u2=630、u3=793、u4=3 255为初始聚类质心。区别在于中值预处理聚类质心的变化，如表2所示，数据1需要进行3次聚类质心变化，可确定聚类质心为u1=81、u2=534、u3=932、u4=3 762，而数据2则需要进行4次聚类质心变化，才能确定。

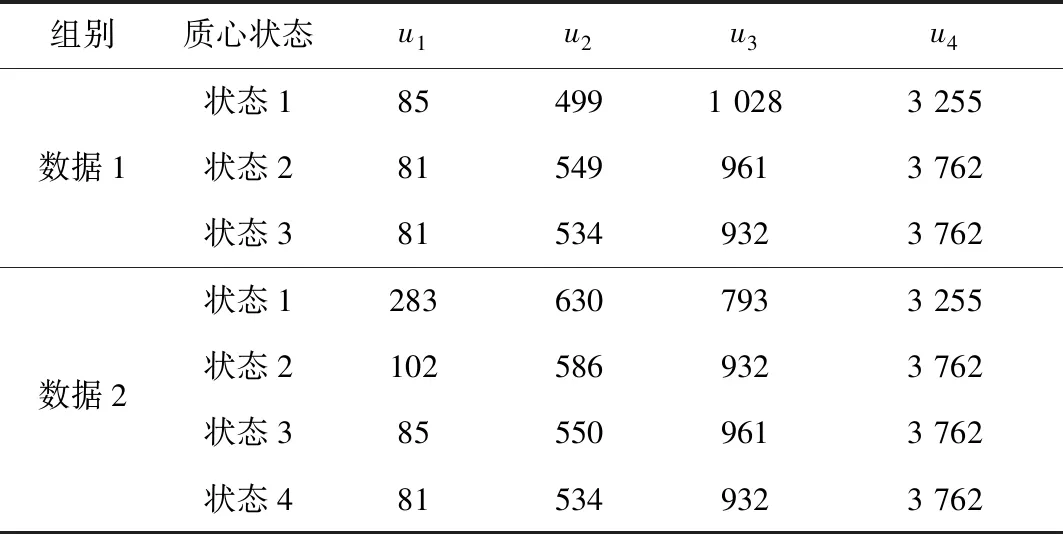
表2 预处理K-means算法聚类质心变化过程

进而确定数据集合S1、S2、S3、S4分别为{x1，x2，x3,… ，x56}、{x57，x58，x59,… ，x70}、{x71，x72，x73,… ，x77}、{x78，x79，x80,… ，x100}，统计得到m1=56、m2=14、m3=7、m4=23；最后计算获得H1=5.6 m、H2=1.4 m、H3=0.7 m、H4=2.3 m，计算结果与油水液位实际测量结果一致，改进K-means算法应用于油水界面测量的准确率得到验证。

4 算法对比分析

4.1 对比结果

为了对比K-means算法和改进K-means算法的性能优劣，以图3提供的样本油水界面数据和图4提供的伪数据作为实验数据，实验在ThinkPad R400电脑(Intel(R)Core(TM)2 Duo CPU P7570，2.26 GHz，RAM 2GB)上进行。选择不同油水界面数据作为K-means算法和改进K-means算法的聚类质心。u1在{x1，x2，x3,… ，x56}内任意取值，u2在{x57，x58，x59,… ，x70}内任意取值，u3在{x71，x72，x73,…，x77}，u4在{x78，x79，x80,…，x100}内任意取值。按照上述聚类质心取值范围可知，K-means算法和改进K-means算法分别运行126 224次。两种算法运行结果如表3所示。

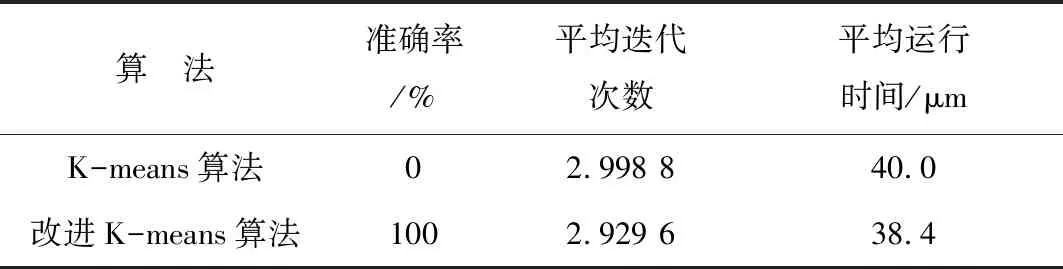
表3 算法运行结果对比

4.2 算法准确率分析

由2.3小节的伪数据分析，以及K-means算法和改进K-means算法的验证结果分析可知，K-means算法直接应用于存在伪数据的油水界面数据，得到的结果受到伪数据的影响，结果出现较大偏差，计算结果不准确；而将改进K-means算法应用存在伪数据的油水界面数据中，可以有效屏蔽其中的伪数据，得到的计算结果与实际测量结果一致，计算结果准确。

4.3 算法迭代次数分析

K-means算法处理油水界面数据时，对于油水界面数据呈现较大的波动数据，算法的执行过程复杂，需反复递归，实验结果总迭代次数需378 521次，迭代次数较多；而改进K-means算法处理油水界面数据时，油水界面数据已经得到优化，优化后的数据呈现大幅波动的情况较少，数据相对平滑，算法的执行过程简单，实验结果总迭代次数需369 781次，迭代次数较少。

4.4 算法运行时间分析

统计2种算法运行时间，实验结果为K-means算法平均耗时5.048 ms，改进K-means算法平均耗时4.851 ms。由此可知，K-means算法和改进K-means算法在运行时间上差距不大，改进K-means算法略优于K-means算法。因K-means算法缺少对油水界面数据的预处理环节，运行时间应快于改进K-means算法，但改进K-means算法总的迭代次数要少于K-means算法。因此，结果表明改进K-means算法运行时间小于K-means算法。

5 结论

本文通过分析油水界面数据来源及其数据特性，提出应用K-means算法计算油水界面。然而发现油水界面中存在伪数据，直接应用K-means算法进行油水界面数据分类统计，结果会存在较大误差。又提出改进K-means的油水界面测量预处理聚类算法，并将其应用于可能存在伪数据的油水界面测量中。通过改进K-means算法描述、算法结果准确率验证和算法对比结果分析，可知预处理K-means算法能够有效处理油水界面伪数据问题，获得正确结果，且算法在算法准确率、算法迭代次数和算法运行时间上均优于K-means算法。