基于压电复合材料的梳状柔性宽带表面波传感器有限元设计

2019-07-17赵华民何存富

仪表技术与传感器 2019年6期

赵华民，何存富，吕炎

(北京工业大学机械工程与应用电子技术学院，北京 100124)

0 引言

厚壁管道作为热电机组不可或缺的关键部件之一，其安全性对于电厂的正常运行具有重要意义。由于制作工艺不完善和使用过程中的腐蚀等原因，厚壁管道内外壁常存在各种缺陷，给电厂的安全运行带来隐患。传统的无损检测技术采用逐点检测，效率低，难以满足实际检测需求。而超声导波技术，作为一种新型的无损检测技术，具有检测距离远，检测效率高等优点，特别适合管道和板结构的检测[1]。作为超声导波是一种，表面波具有在光滑曲面上远距离传播而不出现反射的优点，特别适合管道内外壁缺陷检测[2-4]。

压电梳状传感器是导波激励的常用传感器，通过调整传感器的阵元间距，可以实现不同模态导波的激励。Rose[5]等在理论和实验方面研究了通过改变不同的参数来应用梳状传感器激励导波进行无损检测。Kannajosyula[6]等在波数域内得出了要激励特定模态导波时激励信号的最小相位和时延值，并且得到了模态波长和压电环宽度的对应关系。Glushkov[7]等通过在一系列同轴的环形压电片上施加特定周期和幅值的正弦脉冲波，实现板上导波模态选择。Koduru[8-9]开发了环状PVDF时延技术进行模态的控制，向四周均匀激发Lamb波进行板上的缺陷检测。梳状传感器管道检测方面，Li[10]建立了8通道时延系统来控制不同压电片的激励能量、时间延迟和信号相位，用来增大需要的模态，抑制不需要的模态。Bareille[11]等在管道一端布置16片压电材料，利用压电片剪切振动，激励T模态进行管道缺陷检测。Chang[12]等通过使用PZT和较软的环氧树脂制作了等间距柔性梳状传感器，实现了测量聚苯乙烯试块圆孔的功能。但是以上等间距梳状传感器的某一间距只能激励某一波长的导波。由于单一波长的导波只对某一尺寸范围内缺陷敏感[13]，所以无法满足实际检测的需求。为此需要研制一种宽带传感器，能够激励多种不同频率的导波，以检测不同尺寸的缺陷。所以本文研制一种宽带非等间距梳状表面波传感器，以检测厚板和厚壁管道内外壁缺陷。

一般来说，宽带与窄带没有严格的标准，是相对的概念。如图1所示，定义信号的-3 dB带宽为B=f2-f1,信号中心频率为f0，如果B/f0<0.1为窄带信号，反之为宽带信号。

图1 宽带信号示意图

传统的等间距SAW滤波器要实现宽带滤波效果，常采用倾斜型叉指的形式[14-15]，称为SFIT。其结构如图2(a)所示。其叉指电极采用倾斜形式，在带宽区间内形成n个频带fn,每个频带都满足pi=c/fi。利用多个频带的耦合实现了宽带滤波效果。本传感器为了达到宽频带的设计目标，采用相似形式。通过调整传感器阵元外形和尺寸，采用非矩形阵元的方式，让阵元的多个谐振频率出现在需要的频带范围内，通过多个频带的耦合实现传感器的宽频带激励。传感器阵元形状如图2(b)所示。本研究团队在前期的工作中已经研究了等间距梳状表面波传感器的参数[16]，得出压电阵元采用厚度振动型式，阵元个数等于5，阵元间距等于λR，阵元宽度等于λR/2。所以设置非等间距传感器阵元从左向右分别编号为1-5号。传感器阵元宽度和间距采用由上到下逐渐变化的型式。以3号阵元中线为y轴，以阵元长底边为x轴建立笛卡尔坐标系。传感器阵元以y轴为对称轴。梯形下底边和上底边宽度分别为a1和a2，间距为p1和p2，阵元长度为l。阵元宽度和间距从下底边到上底边逐渐变化，分别对应最低频带和最高频带。中间不同阵元宽度对应不同传感器频带fi，同样任意频带都满足pi=c/fi。当传感器激励频带在500 kHz～1 MHz之间时，计算得到a1=3 mm，a2=1.5 mm，p1=6 mm，p2=3 mm。本文选择1-3型压电复合材料作为传感器阵元材料，通过采用变化阵元的厚度和长度，实现传感器的宽频带激励。

(a)SFIT

(b)非等间距梳状传感器图2 非等间距梳状传感器示意图

1-3型压电复合材料具有高压电性，低阻抗，较高的厚度机电耦合系数Kt和较低的机械品质因子等优点，利于制作宽带传感器。国内外许多学者已经对压电复合材料的宽带传感器进行了研究[17-19],取得了良好的效果。

1-3型压电复合材料的压电相比例和阵元宽高比会对复合材料的振动模式产生影响，为了使传感器阵元只产生厚度振动模态，需要对复合材料的压电相比例和宽高比进行优化。所以本文首先采用有限元建模研究压电复合材料参数。

1 压电复合材料参数的确定

1.1 宽高比和体积百分比的确定

为节省有限元计算时间，Hayward教授[20]提出了周期型模型算法，只计算复合材料一个周期的1/4结构就可以得到与完整结构相同的结果。本文采用相同的方法，用PZflex软件建立如图3所示1/4模型，研究压电复合材料的宽高比和体积百分数对压电复合材料的影响，压电相采用PZT-5H，树脂相采用环氧树脂，材料参数如表1所示。

图3 1-3型压电复合材料的1/4周期有限元模型

表1 聚合物相材料参数

本传感器采用压电材料的厚度震动型式激励表面波，所以1-3型压电复合材料的厚度机电耦合系数Kt越大越好。为加强传感器和钢制管道表面的耦合，需要传感器声阻抗尽可能大，根据式(1)，声阻抗与材料的密度相关，密度越大，声阻抗越大。而1-3型压电复合材料的密度与压电相体积百分比成正比[21]，压电相体积百分数越高，密度越大，为提高压电材料的声阻抗，需要高的压电相体积百分数。

(1)

当谐振频率为500 kHz时，压电柱长度可以根据公式t=Nt/f计算，为4 mm。当压电柱宽度为0.5 mm时，仿真计算不同压电相体积分数V1的压电复合材料的机电耦合系数Kt。因为压电复合材料的聚合物相对压电相的夹持作用，导致压电相谐振频率降低。所以当PZT-5H压电柱长度为4 mm，体积百分比为60%时，压电复合材料的谐振频率为367.8 kHz，低于设计的频率，所以为提高频率，需要缩短压电柱长度，当压电柱长度等于2.9 mm时谐振频率为511.7 kHz，满足设计要求。同样的方法研究得出1 MHz时对应压电片长度为1.45 mm。

当PZT-5H压电柱高度为2.9 mm时，其组成压电复合材料的阻抗与压电相体积百分数的关系如图4所示。从图4可以得出，当宽高比不变时，随着压电相体积百分数增加，压电复合材料谐振频率增高，但其阻抗值变化不大，说明聚合物相的存在会降低材料的谐振频率。

图4 宽高比为0.17时不同压电相体积分数的阻抗曲线

将计算得到的谐振频率值带入式(2)。

(2)

式中：fs为串联谐振频率，Hz；fp为并联谐振频率，Hz。

计算宽高比固定为0.17时不同体积分数V1的压电复合材料的机电耦合系数，如图5所示。可得，机电耦合系数随着压电相体积分数的增加先增大，后减小，在V1等于50%～70%之间时最大，此时机电耦合性能最好。

图5 宽高比为0.17时不同压电相体积分数的Kt

压电相体积百分数不同，在50%、60%、70%时，不同的压电宽高比时的厚度机电耦合系数如图6所示。由图6可以看出，其厚度机电耦合系数Kt在压电宽高比小于0.6时，基本不随压电柱的宽高比变化而变化。当体积百分比等于50%和60%时，Kt值从宽高比0.6开始变小，体积百分比70%时，Kt值在宽高比0.8时还没有明显的减小，利于增加压电相宽度，减低加工难度。为了得到较高的声阻抗并提高激励性能，所以选择压电相体积百分比为70%。

图6 不同压电相体积百分比时厚度模态机电耦合系数随压电相宽高比的变化图

由于压电相在不同的频率处厚度不同，并且由图2(b)可知，不同频带处的阵元宽度也不同。所以在不同的频带上采取不同的压电柱宽度，以保证宽高比小于0.6。宽高比太小虽然能够保证Kt，但是后期加工困难，并且仿真也会需要更多的计算资源。综合体积比和宽高比2个因素，所以选择压电柱宽度在500 kHz处为0.8 mm。体积比70%时对应每周期宽度等于0.956 mm，1 MHz处压电柱宽度等于0.4 mm，对应周期宽度为0.478 mm，中间各频带的压电相宽度每0.01 mm变化1次，一直变化到0.4 mm。

1.2 1-3型压电复合材料横向模态的频率计算

当压电相宽度等于0.8 mm，压电相体积百分比为70%时，压电复合材料的一个周期宽度d等于0.956 mm。因为传感器主要应用压电复合材料的厚度振动模态，为了避免横向模态的影响，需要对横向模态进行计算。

横向模态的频率计算公式可以通过以下计算方式得到：一阶横向模态的频率公式的表达式如式(3)[22]：

fL1=vphase/d

(3)

式中：fL1为一阶横向模态频率，Hz；vphase为压电复合材料相速度，m/s。

二阶横向模态的频率公式的表达式为式(4)：

(4)

vphase=vRp+VF2·(vRC-vRP)

(5)

(6)

式中：vR为均匀各向同性介质的Rayleigh波速，m/s；vRp为聚合物材料的Rayleigh波速，m/s；vRc压电相材料的Rayleigh波速，m/s；VF为压电相材料的体积百分数；vt为横波波速，m/s；

通过式(6)可以得到复合材料中VRp=1 065.7 m/s，VRc=2 029 m/s，所以当VF=70%时带入式(5)得到vphase=1 537.7 m/s。带入式(3)和式(4)得到一阶横向模态频率fL1=1.6085 MHz，一阶横向模态频率fL2=2.274 4 MHz。因为传感器设计激励频率在500 kHz～1 MHz之间，所以当压电复合材料体积百分比为70%，d=0.956 mm时，不会受到横向模态影响。当1 MHz时，d=0.478 mm，同样不会受到横向模态的影响。所以周期宽度d满足要求。

2 压电传感器模型建立

根据上文计算得到的压电复合材料参数，结合图2(b)设计传感器阵元如图7所示。

图7 传感器阵元模型

图7为4号阵元的3D模型图,其余阵元模型类似。图中阵元宽端为500 kHz对应的宽度，其中压电相宽度为0.8 mm,周期宽度为0.956 mm。最窄处对应1 MHz宽度，其中压电相周期宽度为0.4 mm，周期宽度为0.478 mm。中间压电相宽度和周期宽度都逐渐过渡，以保证体积比等于70%。阵元总长度l=30 mm。采用非等间距阵元设计的传感器渲染图如图8所示。压电阵元放入3D打印得到的柔性环氧支架中，在阵元上层为背衬材料，厚度为3 mm，压电阵元与被检测工件之间采用铜片做保护层，厚度为150 μm，保护层兼具保护和阻抗匹配的作用。铜的声阻抗介于压电片和钢之间，适合作为保护层。影响保护层层内损失的因素主要是保护层的厚度，保护层的厚度越大，层内能量损失就越多，因此希望保护层的厚度尽可能地小。工程上，保护层的厚度常采取1/4波长，但是要设计出性能比较好的探头，保护层的厚度将不是理论值。而且，本文设计的传感器为宽带传感器，随着频率的变化，波长也在变化，所以最后综合考虑各种影响因素，选择厚度在150 μm厚铜箔作为保护层。

(a)组装图

(b)爆炸图1—背衬；2—磁铁；3—柔性支架；4—压电复合材料；5—保护层图8 非等间距传感器渲染图

3 传感器性能测试

宽带传感器最重要的指标为频率响应和指向性，频率响应直接关系到传感器的带宽，指向性越好，越利于缺陷检测。下面通过建立3D仿真模型，测试传感器的频率响应和指向性。

3.1 仿真模型建立

在PZflex中建立如图9所示模型，钢板尺寸如图9所示。图9中信号接收点距离传感器中心距离为100 mm，图中圆点为测量传感器频率响应的信号接收点。材料参数如表1所示。背衬采用软件内置Back25材料，为环氧树脂与钨粉的混合材料，25代表钨粉占比为25%。激励信号采用五周期汉宁窗调制正弦波。

图9 梳状传感器仿真模型

3.2 传感器频率响应测试

在500 kHz～1 MHz之间，每隔50 kHz对传感器进行激励，在图9中的信号接收点接收时域信号，比较不同激励频率时传感器激励信号的幅值大小，绘制频率响应曲线。如图10所示，-3 dB带宽约为420 kHz。带宽达到设计要求。

图10 梳状传感器频率响应图

3.3 传感器指向性测试

传感器形成指向性的条件是在发射空间的远场区。传感器的远场区一般定义为rλ>(L/2)2的区域，L代表阵元长度，λ为表面波波长。所以在r=100 mm处，属于远场区域。定义指向性函数为式(7)：

(7)

式中Ur(θ)为r=100 mm处与阵元中线夹角为θ处质点的位移。

如图11所示。在圆周上每隔10°提取表面波信号然后归一化，做传感器指向性图，如图12所示。由图12可以看出，非等间距传感器指向性发生了偏转，表面波能量在-90°方向大于90°方向，传感器Θ-3 dB波束宽度约为30°，能够满足缺陷检测需要。

表面波能量最大值出现在-10°方向的原因为，梯形下底边的宽度相比上底边大，与钢板的接触面积大，能够产生更大的能量，所以产生指向性偏转。

图11 传感器指向性研究模型

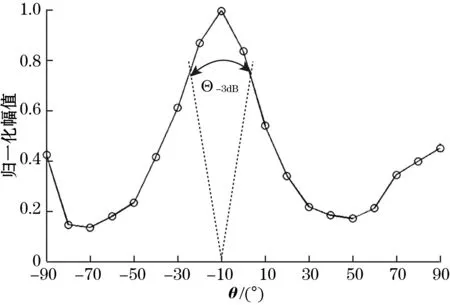
图12 传感器指向性图

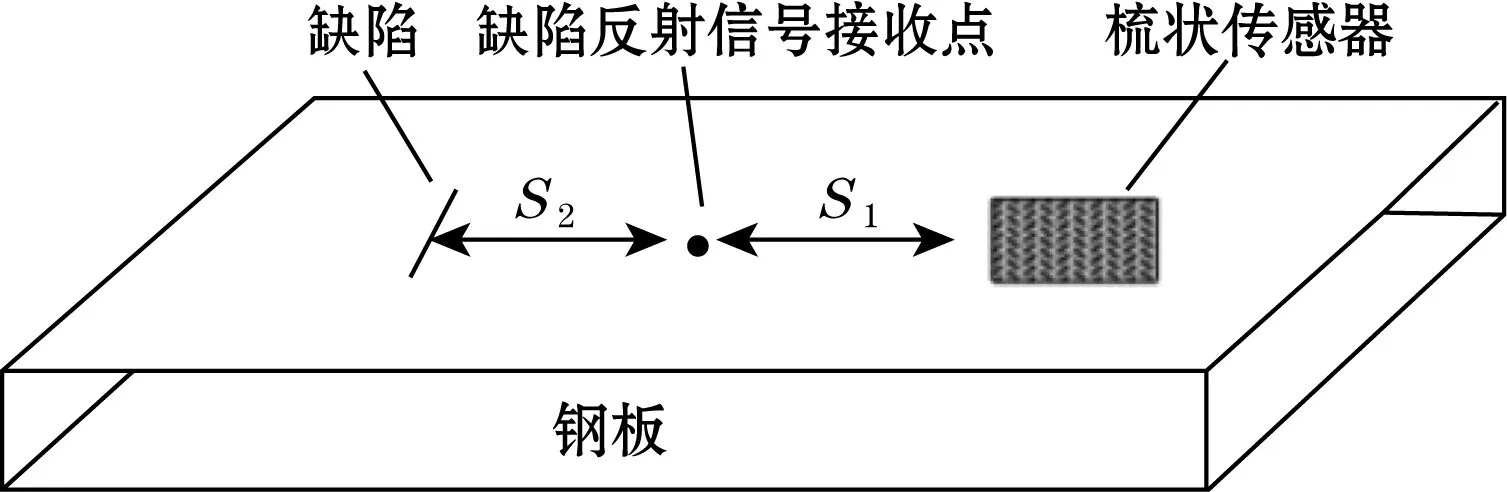
图13 钢板缺陷检测仿真设置图

3.4 传感器缺陷检测

采用仿真得到的最佳传感器参数，进行板上缺陷检测仿真研究。缺陷检测模型如图13所示。缺陷尺寸(长×宽×深)为25 mm×1 mm×1 mm。图中S1为激励传感器与缺陷回波信号接收点的距离设置为50 mm，S2为缺陷回波信号接收点到缺陷的距离同样设置为50 mm。分别用梳状传感器激励500、750 kHz和1 MHz的表面波信号。

分析接收到的缺陷回波如图14所示。通过时间计算，可得波包1为直达波信号，波包2为缺陷回波信号。

由图14可以看出，在不同频率下都可以得到明显的缺陷回波信号。表面传感器具备在多频带下检测缺陷的能力。