基于BA优化核参数的非线性Volterra滤波方法研究

赵 玮，王 强，何晓晖，袁 媛

(1.陆军工程大学国防工程学院，江苏南京 210007；2.陆军工程大学野战工程学院，江苏南京 210007)

0 引言

由于机械振动、传感器数据传输误差以及环境等因素的影响，在实际信号获取、传输与处理过程中常常受到噪声的污染，因此信号降噪在机械状态监测领域内受到众多学者的关注[1]。在信号降噪滤波的方法中，中值滤波、均值滤波、小波滤波以及维纳滤波等方法均得到了广泛的应用[2]。均值滤波作为一种线性滤波方法，对含高斯噪声的信号具有很好地降噪效果，但对冲击噪声无法进行有效的滤除[3]；中值滤波作为一种非线性滤波方法，能够很好地滤除含脉冲干扰的噪声，但对高斯噪声的滤除效果不明显[4]；小波滤波本质是具有多通道带通滤波器，其优势在于分离目标信号与噪声的频带相互分离时的确定性噪声情况，当目标信号与噪声频带重叠情况下，降噪效果不佳[5-6]；维纳滤波为一种线性滤波器，主要用于提取滤除平稳噪声所污染的信号[7]。

在工程实践中，噪声具有相互叠加与影响的特点，含有多种噪声信号，如高斯噪声和冲击噪声等，单一的滤波方法无法对噪声实现有效的滤波[8]。针对混合噪声的滤波方法，多采用将噪声分类后结合不同滤波算法分别对分类后的噪声进行滤除，在信号降噪过程中取得了较单一滤波算法更好的效果，但对噪声的分类与检测导致算法计算量的增加，在需要实时降噪的场合无法得到有效应用。Volterra级数模型具有的线性和非线性项的特性，使得Volterra滤波器综合了线性滤波器、非线性滤波器以及预测的功能，具有很好的同时滤除高斯噪声与冲击噪声的功能，同时还可以满足系统实时性的要求[9-10]。Volterra级数的核参数是描述非线性系统的关键，其辨识精度直接影响滤波器的性能。在核参数辨识研究方面，群智能优化算法在Volterra级数的时域核参数辨识方面受到广泛的关注，甘慧萍[11]等提出一种基于遗传算法辨识Volterra滤波器核参数的机械振动信号消噪方法，在获得最优的核参数的同时对含高斯噪声和脉冲干扰的机械振动信号进行消噪处理，具有很好的滤波性能和鲁棒性。李宁洲[12]等提出一种动态随机局部搜索生物地理优化算法(DRLBBO)优化求解模型的核参数的非线性Volterra滤波方法，有效滤除了车轮转速信号所含混合噪声；同时提出了动态多子群引力搜索算法和灰聚类多子群自适应粒子群算法，实现了非线性Volterra滤波器模型结构和参数的确认及优化求解[13]。冯晓云[14]等提出了一种基于组合混沌策略自适应量子微粒群算法(CCSAQPSO算法)的Volterra时域核辨识方法，其核参数辨识精度高，同时在全局优化能力和快速收敛能力上都有较大提高。本文提出一种基于蝙蝠算法(BA)的核参数优化的非线性Volterra滤波方法，在建立能够定量反映待辨识模型输出与理想输出之间的偏差程度的适应度函数的基础上，获得优化核参数的同时对含有混合高斯噪声与脉冲噪声的信号进行降噪处理，通过仿真实验验证，该方法在针对混合噪声的滤除方面具有很好的效果。

1 非线性Volterra滤波器模型

Volterra级数模型一种用输入u(t)与输出y(t)表示的非线性系统模型，其关系可以表示为

(1)

式中：

式中hn(τ1,τ2,…,τn)为非线性Volterra滤波器模型的n阶时域核。

在信号滤波过程中，首先需要将式(1)所示的无穷阶Volterra级数模型进行离散化处理，获得离散化n阶Volterra滤波器模型：

(2)

式中：N为最高阶次；k为Volterra级数阶次，取值为正整数；e(k)为截断误差。

yn(k)可以表示为

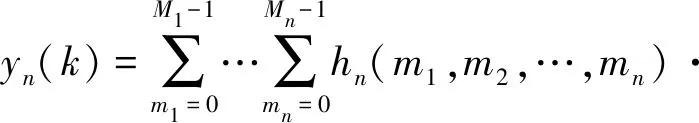
(3)

式中：mi为记忆长度；hn(m1,m2,…,mn)为n阶Volterra时域核函数。

在滤波过程中，式(2)无穷级数的特点导致其无法精确的计算，通常进行阶段处理，即确定无穷级数的阶数k与记忆长度mi，通常利用前3阶Volterra 级数模型即可近似描述很多实际非线性系统，满足非线性滤波器的要求，因此最高阶次N=3，则式(2)可化简为

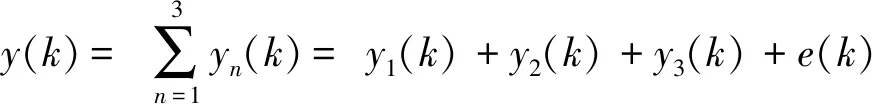
(4)

由于Volterra 级数的时域核具有对称性，即：

(5)

式中i1,i2,…，in为1，2，…，n中的任一排列。

(6)

式中ai为考虑时域核对称性后引入的权系，且

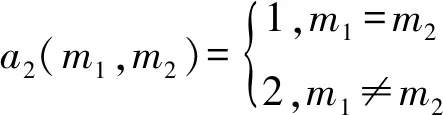
三阶滤波器的模型可以表示为

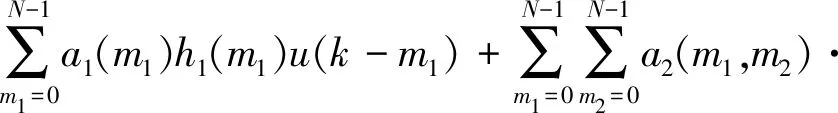
h2(m1,m2)u(k-m1)u(k-m2)+

u(k-m1)u(k-m2)u(k-m3)+e(k)

(7)

式中，记忆长度mi取适当值时，在误差允许范围内，e(k)取值可以忽略不计。

2 信号非线性Volterra 滤波器模型核参数优化

非线性Volterra 滤波器模型的核参数优化实质上是一个多维参数空间上的寻优问题，蝙蝠算法(BA)作为一种常用的群智能优化算法[15]，本文研究一种用BA 算法对非线性Volterra滤波器模型的核参数进行优化。基于蝙蝠算法的Volterra 滤波器的方法：将Volterra滤波器的模型结构与参数辨识看作优化问题，将核参数作为优化变量，将输入实际信号向量与核参数向量的乘积与理想信号向量的均方差作为BA算法的适应度函数，利用BA算法通过迭代寻优使待辨识模型输出逼近实际信号输出，求解待辨识模型的核参数。

2.1 BA算法

蝙蝠算法是由Yang提出的一种利用蝙蝠在觅食时所发出的脉冲的频率、响度、脉冲发射率的变化，模拟蝙蝠回声定位行为的群智能算法[16]。蝙蝠算法是通过频率的调整引起波长的变化，波长的大小与蝙蝠所捕食的昆虫的大小相一致，从而可定位目标。蝙蝠按脉冲发射率和响度发出声波脉冲，当发现目标时会增加脉冲的发射率，减小响度，从而逼近目标捕食猎物。在求解优化问题时，将待优化问题的目标函数值衡量蝙蝠所处位置的优劣，则蝙蝠的空间位置以及速度更新公式为

(8)

式中：t为迭代次数；Xi(t)为t时刻蝙蝠位置向量；Vi(t)为蝙蝠的t时刻飞行速度向量；Xbest(t)为当前群体中所有蝙蝠中最优位置；fi为蝙蝠i搜索猎物时使用的脉冲频率，fi∈[fmin,fmax]；[fmin,fmax]为搜索脉冲频率范围；β∈[0，1]为均匀分布的随机变量。

(9)

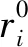
(10)

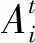
蝙蝠算法流程如下：

(1)初始化算法基本参数。确定蝙蝠数目m，搜索脉冲频率范围[fmin，fmax]，最大脉冲音强A,音强衰减系数α,最大脉冲频度r0，脉冲频度增加系数γ，最大迭代次数MaxT；

(2)初始化第i只蝙蝠的位置Xi和速度Vi，初始化蝙蝠搜索脉冲频率fi和音强Ai，计算每只蝙蝠的初始适应度值；

(3)通过调整频率运用式(8)更新蝙蝠速度Vi与位置Xi；

(4)生成随机数rand1，若rand1>ri，选择当前个体的最优个体Xbest(t)，并对最优位置蝙蝠进行随机扰动，通过随机扰动产生一个局部个体Xnew(t)，并计算适应度值；

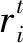
(6)对蝙蝠群体进行评估，找出当前最佳蝙蝠以及所处空间位置。当满足搜索精度或达到最大搜索次数，输出全局最优个体值；否则返回(3)进行循环。

2.2 基于BA算法核参数优化

采用BA算法进行非线性Volterra 滤波器模型核参数优化，待优化的核参数向量表示为

H=[h1(0),h1(1),…,h1(M1-1),h2(0,0),h2(0,1), …,H2(M2-1,M2-1),h3(0,0,0),h3(0,0,1)， …,h3(M3-1,M3-1,M3-1)]

(11)

作为蝙蝠算法的个体位置，蝙蝠搜索空间维度D表示为

(12)

输入矩阵U=[u(k),u(k+1),…,u(k+L-1)]T，其中L为数据长度，u(k)为k时刻输入向量，u(k)如式(13)所示：

u(k)={u(k),u(k-1),…,u(k-M1+1),

[u(k)]2,u(k)u(k-1),…,[u(k-M3+1)]2}T

(13)

则寻优的目标函数

HIS(Xi)=f[u(k)-ud(k)]

(14)

式中ud(k)为理想信号。

采用BA算法使式(14)取得最小值的最优蝙蝠位置即非线性Volterra滤波器模型的最优核参数，其优化流程如图1所示。

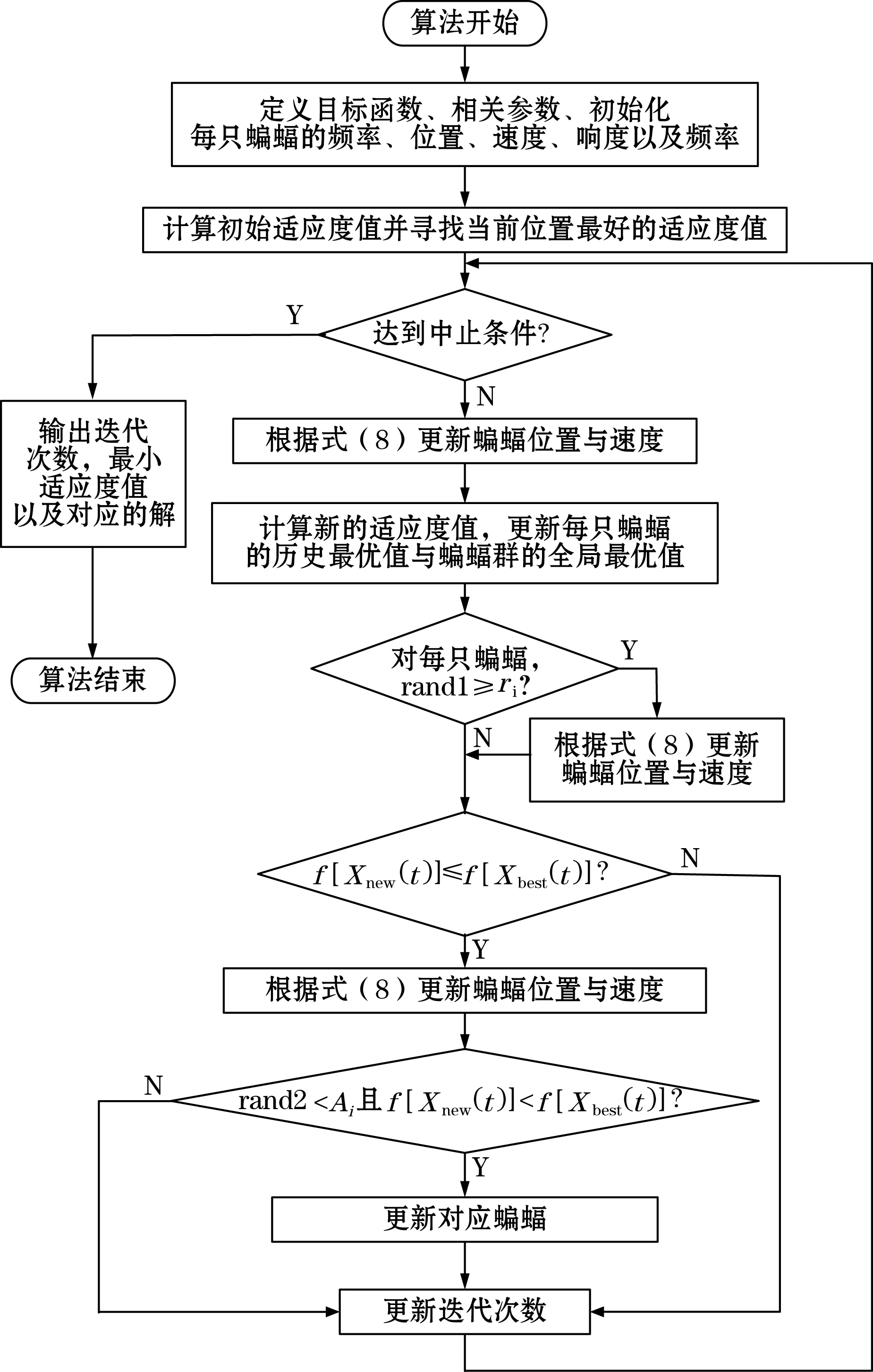
图1 基于BA算法的Volterra滤波器模型核参数优化流程

3 仿真与实验验证与结果分析

为了验证基于BA优化核参数的Volterra滤波器在消除噪声方面的有效性，分别对基于中值滤波器、均值滤波器、维纳滤波器以及基于BA算法优化核参数的Volterra滤波器的降噪效果的进行仿真实验验证。仿真实验中，采用式(15)所示的数学模型模拟机械振动信号，其原始不含噪声信号和加噪声信号分别如图2(a)、图2(b)所示。

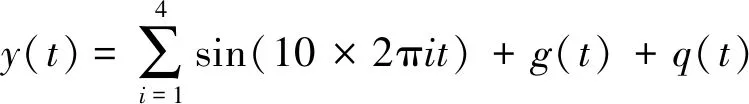
(15)

式中：g(t)为模拟信号添加的信噪比为10 dB的高斯白噪声；q(t)为5 dB冲击噪声信号。

含添加噪声的信号如图2(b)所示，采样周期为0.1 ms，蝙蝠算法中蝙蝠种群个数为20，搜索脉冲频率范围为fi∈[0,10]，最大脉冲频度r0=1，最大脉冲音强A0=0.4，脉冲音强衰减系数α=0.95，脉冲频度增加系数γ=0.1，迭代次数为900。

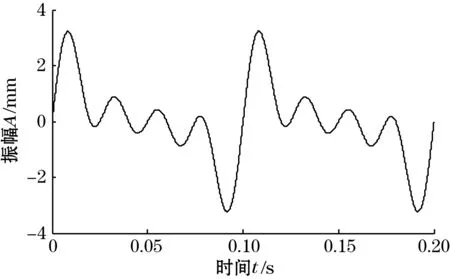
(a)不含噪声信号

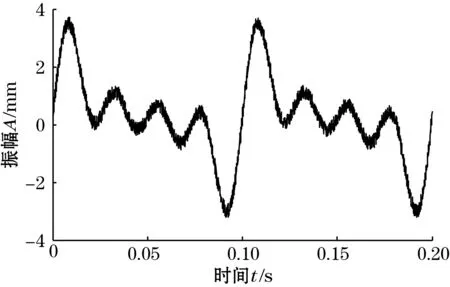
(b)含噪声信号图2 原始信号与含噪声信号

分别采用中值滤波、均值滤波、维纳滤波以及基于BA算法的优化核参数的Volterra滤波对含噪声的信号进行滤波仿真实验，其结果如图3所示。

由图3(a)可以看出，运用中值滤波的方法，能很好地滤除脉冲噪声，但是高斯噪声的滤除效果不明显；由图3(b)可知，运用均值滤波的方法进行信号降噪，较中值滤波对高斯白噪声滤除效果较好，但对于冲击噪声滤除效果较差；由图3(c)可知，用维纳滤波器滤波后进行消噪，滤波结果不能很好地反映原始信号特征，信号存在失真现象；由图3(d)可知，运用基于BA优化核参数的非线性Volterra滤波器进行信号降噪，能够很好地滤除高斯白噪声与冲击噪声，比传统的滤波方法在滤除组合噪声方面效果好，滤波结果更接近原始信号，信号失真小，特别是针对振动信号降噪方面具有一定的优势。

4 结论

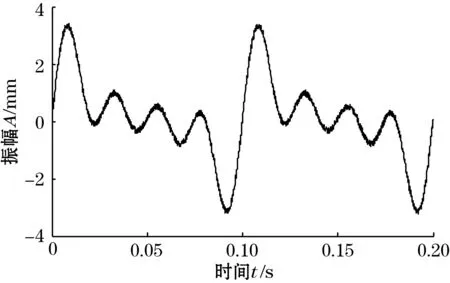
(a)中值滤波后的信号

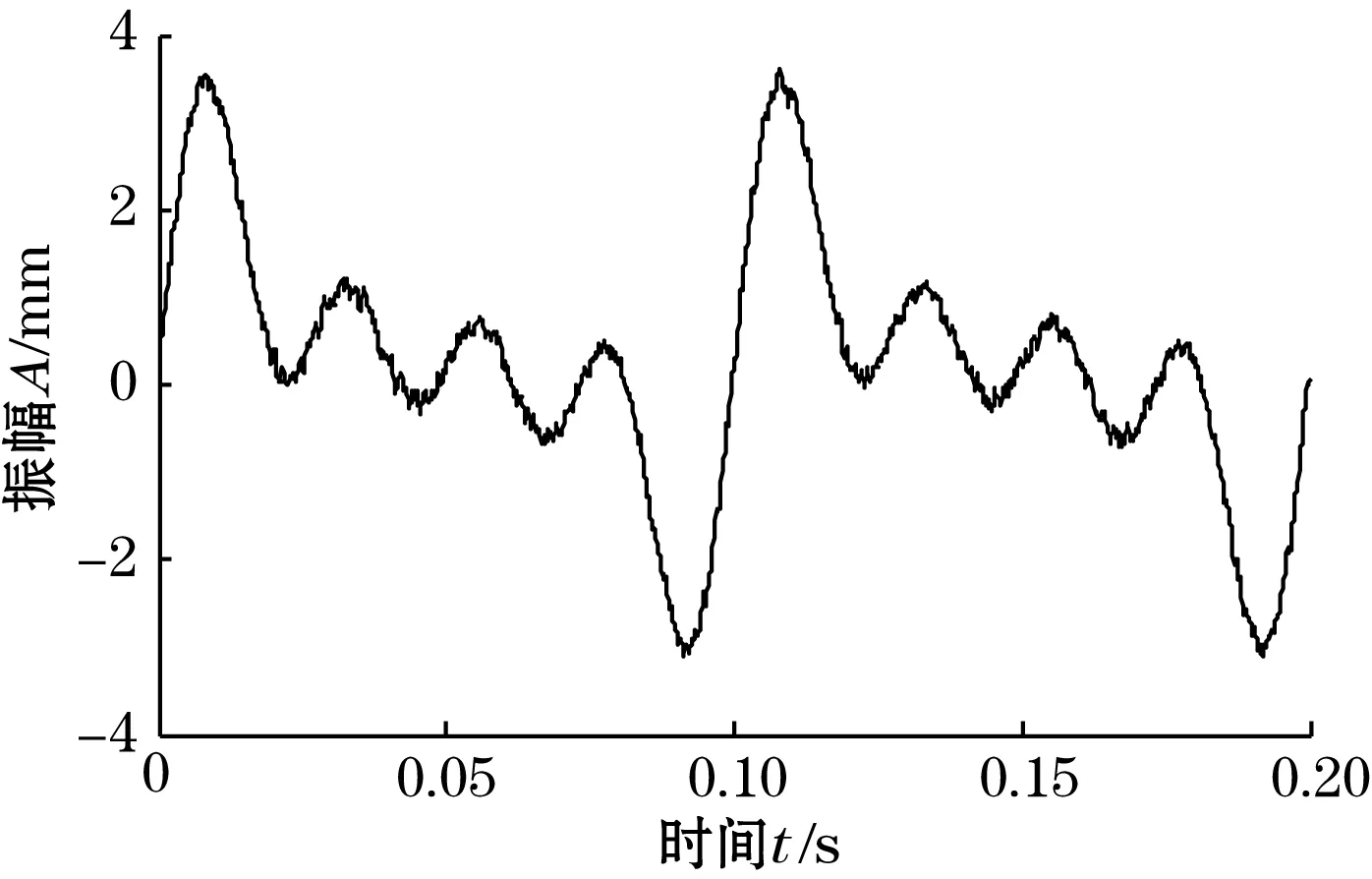
(b)均值滤波后的信号

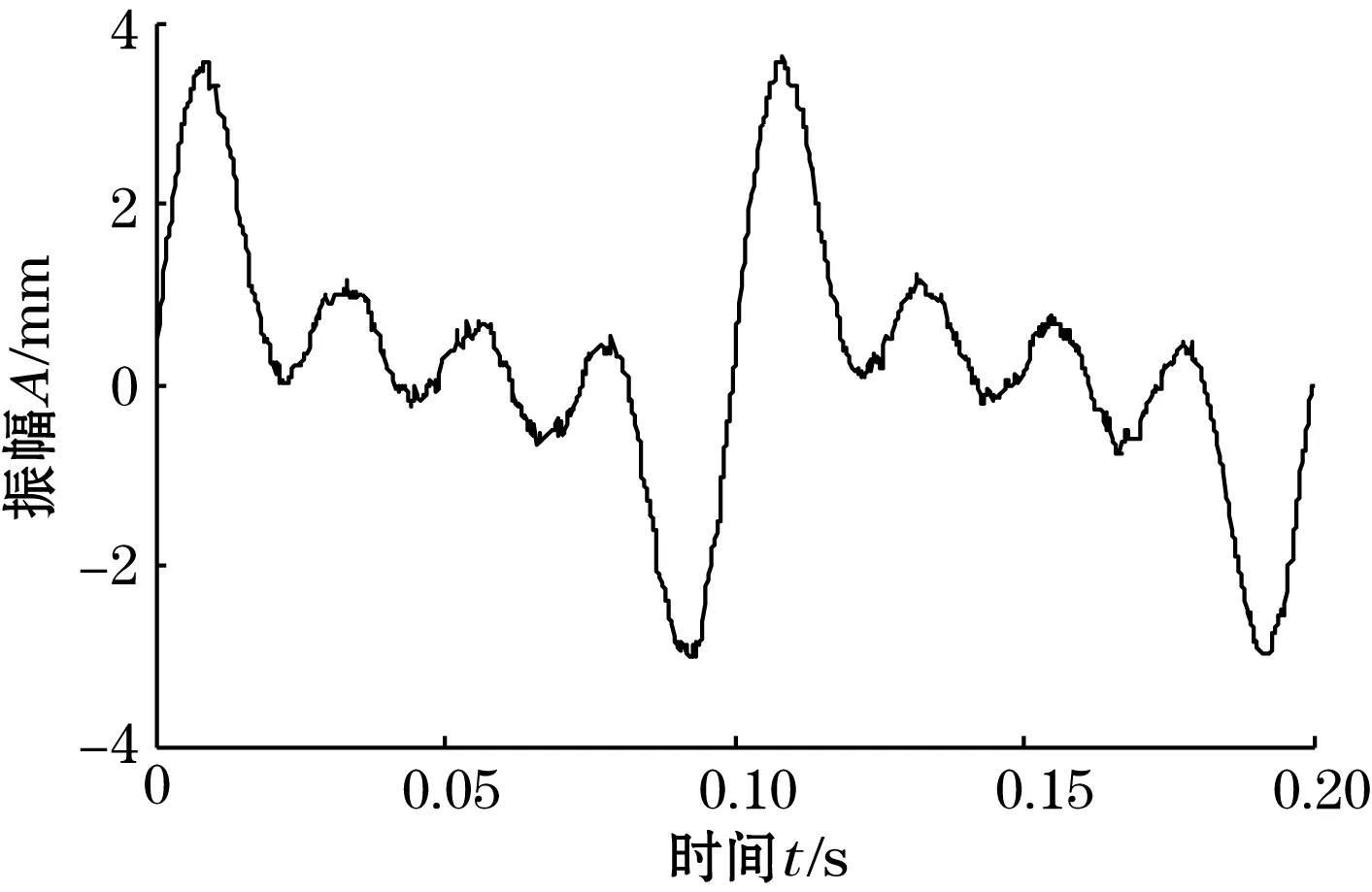
(c)维纳滤波后的信号

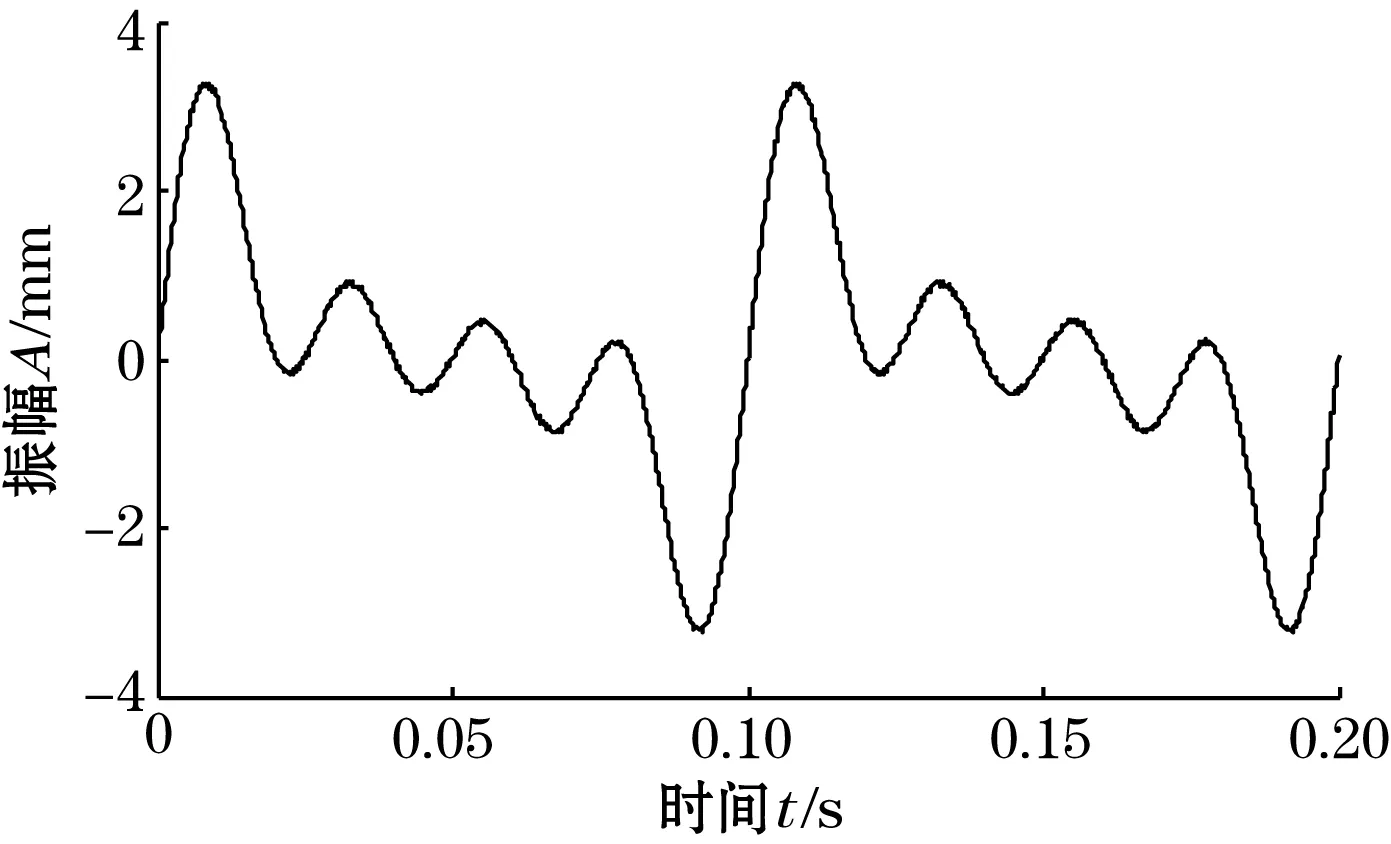
(d)基于BA优化核参数的Volterra滤波后的信号图3 经滤波后信号

本文针对含有混合噪声的信号降噪的问题，提出了一种基于蝙蝠算法优化核参数的非线性Volterra方法，在满足适应度函数取得最小值的情况下，运用BA算法迭代求解相应的最优非线性Volterra滤波器模型核参数。仿真结果表明，基于BA优化核参数的非线性Volterra滤波器兼具线性与非线性滤波器的优势，较单一的传统滤波算法如中值滤波、均值滤波、维纳滤波等具有对含高斯噪声与冲击噪声的混合噪声更好的滤波性能，且信号失真现象不明显，同时较组合滤波方法具有运算量小的特点，可以用于对信号处理有实时性要求的场合。