模糊PID在逆变电源功率控制上的应用

王俊仃　邱秀荣　侯严严

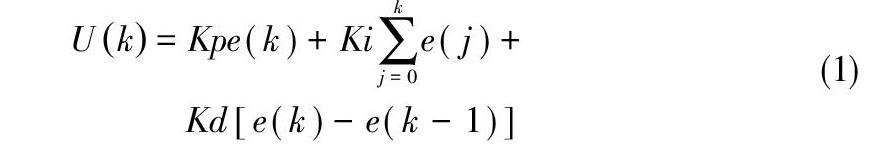
摘要：针对常规PID在逆变电源调节中的不足，提出了一种在高频逆变电源控制中把模糊控制理论与传统PID相结合的模糊PID控制。对模糊PID理论推导，并把模糊PID与传统PID在MATLAB/Simlink环境下仿真对比。最后把模糊PID模块应用在逆变电源系统中，在Simlink仿真环境下完成了输出逆变功率的控制。证明模糊PID有效地提高了输出波形的稳态精度和动态响应。

关键词：逆变电源;PID;模糊控制;模糊PID

中图分类号：TM74          文献标识码：A

文章编号：1009-3044（2019）15-0274-03

Abstract： Aiming at the deficiency of conventional PID in the regulation of inverter， a fuzzy PID control method combining fuzzy control theory with traditional PID is proposed in the control of high frequency inverter. By inferring the theory of fuzzy PID and simulating in the MATLAB/Simlink environment， fuzzy PID is compared with traditional PID. Finally， by using fuzzy PID module in the inverter system， the inverter power control is completed in the Simlink simulation environment. It turns out that the fuzzy PID effectively improves the output waveform on the steady-state accuracy and dynamic response.

Key words： inverter; PID; fuzzy control; fuzzy PID

为了高效地使用电能，许多行业的用电设备都不是直接使用交流电网提供电能，而是根据用电设备的要求采用电力电子技术对电能进行逆变，得到所需的电能形式。这就要求逆变电源要对输出功率，输出电压或电流进行有效的控制。目前国内外使用的主要的控制方法[1]有：无差拍控制、重复控制技术、滞环电流控制、PID控制[2]。其中PID控制结构简单，鲁棒性好，控制精度高，能满足大多数工业要求。

常规的PID控制是为满足一些参数的要求用一组固定的[Kp]、[Ki]、[Kd]调节，它要求被控制对象要有精确的数学模型，其自身又存在超调量大，稳态精度差，而且对于非线性因素引起的参量变化不能做出准确调整的缺点。当逆变电源发生非线性负载引起的参数变化时，常规的PID控制方法就无法做出调节了。随着模糊理论的不断发展，它逐渐表现出对于非线性系统的优越的跟踪能力和对被控制系统不要求有精确的数学模型等优点。把模糊理论与PID相结合的控制系统很好地解决了以上难题[3]。本文在MATLAB/Simlink环境下仿真对比了模糊PID在动静态上的优点。搭建逆变系统，并把模糊PID应用在逆变系统中，证明了其可行性。

1模糊PID

1.1 PID算法与模糊理论

离散后的PID算式如下：

其中[e（k）]是实际值与期望值的差，[U（k）]为第[k]次采样后控制量，[Kp]、[Ki]、[Kd]分别为比例系数、积分系数、微分系数。

[Kp]：通过直接调节偏差的方法减少偏差;[Ki]：为了提高系统的稳态精度加入积分项;[Kd]：代表了偏差的变化趋势，根据该趋势提前引入一个校正信号，加快了系统动作响应。如何找到一个给定系统的三个参数是一个比较烦琐的过程。

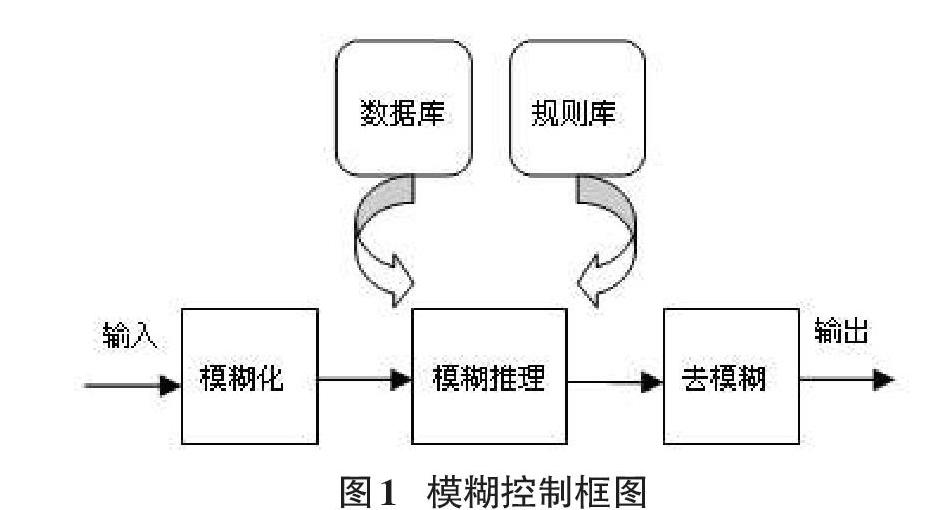
模糊控制理论[4]是以模糊逻辑和模糊数学为基础的，常用来实现非线性、时变系統控制的重要手段，其控制过程示意图如图1。

模糊化，把在某个范围内的输入量先归一化到模糊论域内，如输入量的精确值变化范围是[-20，20]，模糊论域是[-1，1]，那么当输入为10的时候对应的模糊值是0.5。再根据隶属度函数判断0.5属于哪个模糊变量如（PM）。数据库里存放的是模糊变量，规则库里存放的是模糊推理规则。模糊推理则是把输入模糊变量在规则库的规则下推导得到一个对应的输出模糊变量。去模糊是把推导出来的模糊变量经模糊决策转换成具体的输出值的过程。

1.2 控制器设计

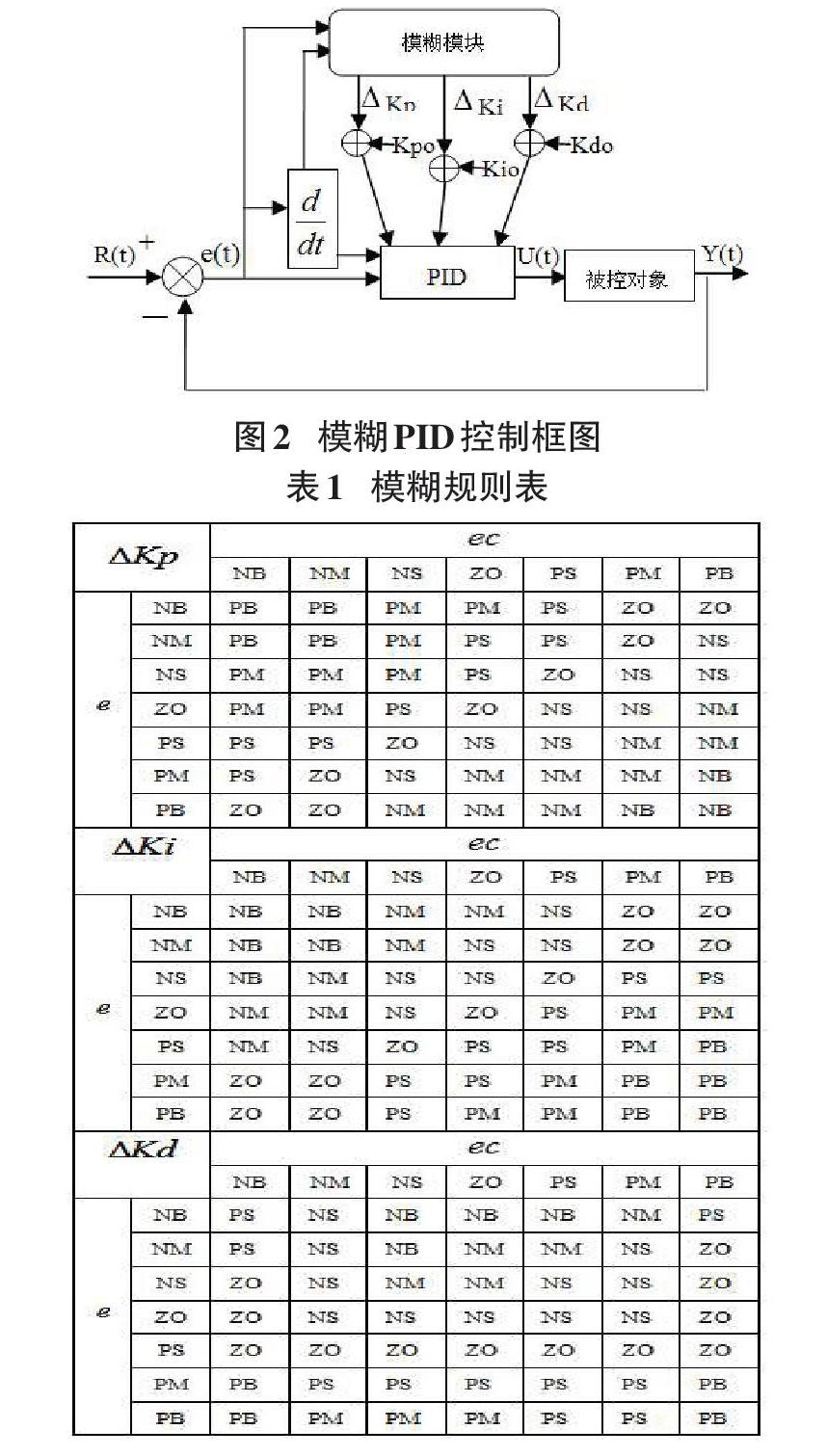
模糊PID控制器是把PID算法和模糊理论相结合，在上一次产生的控制量的基础上，找出PID参数增量（[ΔKp]、[ΔKi]、[ΔKd]）与误差[e]和误差变化率[ec]之间的模糊关系，查询模糊矩阵表1，利用模糊规则进行模糊推理，进而得到不同时刻的[e]和[ec]对应的PID参数增量，把得到的增量与初始[Kpo]、[Kio]、[Kdo]相加得到[Kp]、[Ki]、[Kd]，其框图如图2。

把[e]、[ec]作为输入变量其对应的模糊论域为（-6，6），模糊语言变量分别用负大（NB）、负中（NM）、负小（NS）、零（ZO）、正小（PS）、正中（PM）、正大（PB）表示。[ΔKp]、[ΔKi]、[ΔKd]的模糊论域设为（-3，3），模糊语言变量也用负大、负中、负小、零、正小、正中、正大表示，隶属度函数全选trimf。由于不同的系统[e]、[ec]的具体值是不同的，为了充分的利用模糊论域需要把[e]、[ec]的值乘以一个系数归一化到模糊论域里，同理也需要把去模糊化后的数乘以一个量化因子，得到应调节的实际数值。如图4 为[ΔKp]的隶属度函数编辑器。

根据模糊规则表分别编辑[ΔKp]、[ΔKi]、[ΔKd]的49条模糊规则，如下图5为[ΔKp]的模糊规则编辑器。

2模糊PID建模与仿真

在Simlink下搭建模型仿真，对比模糊PID与常规PID在阶跃信号下的响应波形。设逆变器的负载为LLC负载，等效为电阻与电感串联。谐振负载的传递函数为：

图6中，模糊PID模块中[e]和[ec]经过增益Gain0、Gain1归一到模糊论域里，分别经[ΔKp]、[ΔKi]、[ΔKd]的模糊模块后再经Gain2、Gain3 、Gain4量化输出。经量化后的实际值再与[Kpo]、[Kio]、[Kdo]相加得到[Kp]、[Ki]、[Kd]在线调整的值，进而调节传递函数。仿真波形如图7所示。

从图7仿真波形的输出结果可以看出，模糊PID在超调量，稳定时间，稳态精度上都优于传统PID。当加入干扰后，可以看出模糊PID使系统更快地进入稳定状态。

3逆变系统建模与仿真

采用电压型逆变系统[5]，系统建模如图8所示，交流电压经过D0-D3和C0整流，变成直流电压。该电压经IGBT与D4、L0、C1组成的直流斩波电路变为大小可调的直流电压。Mos0-Mos3组成全桥逆变器， 再经模糊PID模块控制。设逆变器输出的方波电压、输出有功功率分别为Us、P， Us一定，当[Re[1/Z（w）]]取最大时逆变器输出有功功率最大，此时逆变器输出电压频率[f]等于负载谐振频率[fo]。S-Function模块以等腰三角波为载波，改变逆变器输出方波幅值，仿真模型如图8。

当给定某一功率时，系统输出波形如图9所示。

从仿真结果看出本系统比传统PID控制器更快的稳定在给定功率上。

4结论

模糊PID调功不仅继承了传统直流斩波调功易于控制、开关损耗小、成本低的优点，还有动态响应快、输出功率波动小的优点。对于一些非线性、时变因素引起的功率变动，模糊PID能够很好地实现实际输出功率对给定功率的跟踪，表明了模糊PID在逆变器功率控制上的优越性。

参考文献：

[1] 彭传彪，王少坤，王晓锋，等.自适应滞环电流控制逆变器复合控制策略[J].电力自动化设备，2011，31（7）：42-47.

[2] Bao gang Hu ， George K. I. Mann， and Raymond G. Gosine. New Methodology for Analytical and Optimal Design of Fuzzy PID Controllers[J]. IEEE TRANSACTIONS ON FUZZY SYSTEMS，5（7）：521-539.

[3] 張智娟，李丹丹.模糊自适应PID控制电压型逆变器的研究[J].电源技术，2013，37（12）：2217-2220.

[4] 章卫国，杨向忠.模糊控制理论与应用[M].西北工业大学出版社， 1999.

[5] 韩思亮.基于直流变换器的逆变器拓扑和滑模控制技术研究[D].浙江大学，2005.

【通联编辑：梁书】