一种改进Delaunay三角剖分的辅助节点算法研究

摘要：以无线传感器网络辅助节点为主要研究对象，利用Delaunay 三角剖分技术获得网络节点的基础上，在传感器网络检测的目标区域内含有一些覆盖盲点的情况下，提出了一种能量有效的传感器网络辅助节点配置算法。利用模拟仿真试验表明，与原算法相比，该算法在网络覆盖率及算法运行时间等方面更具一定的优势。

关键词：辅助节点;无线传感器网络;Delaunay三角剖分;覆盖盲点

中图分类号：TP393        文献标识码：A

文章编号：1009-3044（2019）14-0025-02

1 引言

无线传感器网络由大量传感器节点组成，通常它们被密集地布置在要测量的环境中来获取所需的数据信息。传感器节点配置是无线传感器网络研究的核心问题之一。无线传感器节点被广泛应用于一些场景信息监测中，为了提高无线传感器网络的灵活性，延长网络的生命周期，文献[1]运用 Delaunay三角剖分的策略定义了节点之间的邻接关系，并且可以通过 Delaunay三角剖分快速获取节点的邻接节点。文献[2]和文献[3]使用启发式连通支配集算法思想来选择活跃节点。文献[4]使用Voronic划分的减量构造将部分覆盖冗余节点转入能耗较低的睡眠状态，在能量效率、网络声明周期等方面得到了改进。

本文在Delaunay三角剖分的连通算法基础上，提出了一种改进的辅助节点算法（CCV），该算法选择一些节点辅助覆盖构成连通网络，其中覆盖节点和辅助节点都为活跃节点。改进算法在网络覆盖率及算法运行时间优于原算法。

2 輔助节点构造

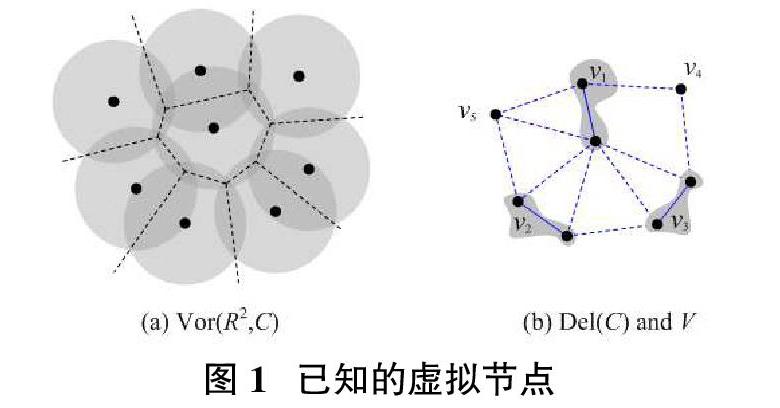
改进算法的Voronoi划分Vor（R2，C）（如图1（a）），构造覆盖集C的Delaunay三角剖分Del（C）（如图1 （b））。使用算法BFS遍历图Del（C）中所有长度不超过Rt的边，获得覆盖集C所有的连通覆盖子集，即每个连通覆盖子集内的任意两节点之间存在一条由覆盖节点组成的连通路径，如图1 （b）的实线所示;用Ci表示第i个连通覆盖子集，每个覆盖子集Ci抽象为虚拟节点vi，将覆盖集C转换为一个虚拟节点集V。如图1（b）所示的图Del（C），转换后的虚拟节点集V为{v1，v2，v3，v4，v5}。

若V仅有一个虚拟节点，则覆盖集C构成连通网络;否则，按照如下步骤选择辅助节点。

第一步：依据CCV算法的Voronoi划分Vor（R2，S）和通信半径Rt，构造初始网络的Unit Delaunay三角剖分UDel（S），如图 2 所示。对图UDel（S）的任意边uv，按照公式cost（u，v）=||uv||a/max（eu，ev）b计算通信代价，其中max（eu，ev）表示节点u和v中剩余能量最大值，指数a和b为非负整数。

第二步：若UDG图为连通图，则UDel图为UDG图的连通子图。将图UDel（S）的每个连通覆盖子集Ci抽象为虚拟节点vi，删除连接节点集Ci中两节点的边;当节点u?Ci与节点集Ci的m（?1）个节点连接时，保留通信代价最小的边连接节点u和虚拟节点vi。经过上述操作后，图UDel（S）变换为一个连通加权图，记为wUDel（S）。

第三步：Del图一个连通图，但一些边的长度超过Rt。将图Del（C）的每个连通覆盖子集Ci抽象为虚拟节点vi，删除连接节点集Ci中两节点的边（即长度不超过Rt的边）;任意虚拟节点vi和vj，图Del（C）存在m（?1）条边连接覆盖集Ci和Cj，保留一条边连接虚拟节点vi和vj，将节点vi和vj在图wUDel（S）中的最短路径Path（vi，vj）上的通信代价作为该边的权值。经过上述操作后，图Del（C）变换为一个连通加权图Del（V），如图3（a）所示。

第四步：使用Kruskal算法构造Del（V）的最小生成树Tree（V），每条边对应的最短路径上的节点即为辅助覆盖集C构成网络的节点，如图 3（b） 所示。

3实验仿真分析

为了评估算法性能，本文用C++实现算法与文献CVT+MST，其中算法CVT求解CVT覆盖节点、算法MST求解MST网关节点。运行环境为P2.0GHz CPU与2G内存;实验场景如下：给定感知半径Rs，在目标区域1000×1000内随机部署n个互不重叠的传感器节点。

理论上，覆盖节点数量将与传感半径Rs有关，辅助覆盖节点构成连通网络的节点数量将与通信半径Rt有关;为此，本文将针对不同的Rt/Rs值，统计评估活跃节点的数量、剩余能量和发射功率以及算法执行时间等指标。

3.1活跃节点的数量

1） 网络覆盖率是指所有网络覆盖目标区域的面积比率。在目标区域内随机部署1000～2000个节点，初始网络的覆盖率如图×所示;当Rs=50时，初始网络的覆盖率超过99.86%，但不会收敛到100%;当Rs=100时，覆盖率将近似收敛于100%;因此，在目标区域内含有一些覆盖盲点的假设下，研究传感器网络的最小连通覆盖具有很强的现实意义。

2） 改进算法CCV求解覆盖集时仅涉及传感半径Rs，即覆盖集的大小由感知半径Rs决定，如图4所示;其中，Rs=50的覆盖节点约为282，Rs=10的覆盖节点约为72。当Rs=100时，网络可以覆盖整个目标区域时，算法CVT求解的覆盖节点稍微大于CCV，但差值不到1;当Rs=50时，网络只能覆盖部分目标区域，算法CVT只能将所有节点设为覆盖节点，其覆盖节点明显大于CCV。

3） 针对Rs=100的情况，分析Rc=50、100、150三种情况下的网关节点，如图5所示。当Rc=50，能够相互通信的覆盖节点不多。

当Rs=100时，实验场景Rc=50、100、150的LCD网关节点分别约为155、33、0.4个，网络部署密度基本上不影响LCD网关节点的大小，如图5（a）所示。

随着通信半径Rc的增大，活跃节点中网关节点的比率RGS逐步减少，特别是Rc/Rs?1.5后的网关节点比率接近0，如图5（b）所示。总的来说， Rc/Rs<0.9时的MST网关节点小于LCD，而Rc/Rs?0.9后的LCD网关节点小于MST，其网关节点比率差<3%。

综合图5可知，给定感知半径Rs与通信半径Rc时，完全覆盖目标区域的活跃节点保持在一定的数量，与网络部署密度无关，为此分析活跃节点的平均能量与平均度时将不考虑网络部署密度。

3.2 算法运行时间

随着节点数量n的增加，CCV运行时间将近似线性增长，而CVT运行时间将近似指数增长，其中CCV运行时间要低于CVT运行时间将近102数量级，如图6（a）所示。

4 展望

本文基于无线传感器网络配置辅助节点问题，利用Delaunay 三角剖分获得网络节点，使用UDel图的连通策略解决活跃节点的连通问题。通过设置辅助节点，提升了节点的覆盖质量，在算法运行时间方面得到了改善。以后的工作将综合考虑传感器网络在选择活跃节点时的网络时延、通信干扰等问题。

参考文献：

[1] Yu X， Huang W， Lan J， et al. A Novel Virtual Force Approach for Node Deployment in Wireless Sensor Network[C] //IEEE， International Conference on Distributed Computing in Sensor Systems. IEEE Computer Society， 2012：359-363.

[2] Torkestani J A. An adaptive energy-efficient area coverage algorithm for wireless sensor networks[J].Ad Hoc Network，2013，11（6）：1655-1666.

[3] 张涛， 余翔宇， 蓝俊健，等. 改进的无线传感器网络节點虚拟力部署方法[J]. 计算机应用研究， 2015 （11） ：3356-3358.

[4] 徐鹏飞，廖明华，张华. 能量有效的传感器网络连通覆盖控制算法[J].小型微型计算机系统，2015，36（10）.

【通联编辑：唐一东】