冰箱压缩机曲柄连杆机构振动分析

(山东科技大学 机械电子工程学院，山东 青岛 266590)

近年来，冰箱制冷压缩机市场发展迅速[1]，在全球范围内，约有99%家用冰箱使用活塞式制冷压缩机[2]。活塞式压缩机具有结构简单、易批量生产和成本低等优点，然而也存在一些尚未解决的问题，比如运行过程中会产生较大的噪声和机械振动[3]。压缩机的核心部件之一是曲柄连杆机构，其不平衡力是产生振动噪声的根源。很多学者对曲柄连杆机构产生的不平衡惯性力进行了研究，如康献民等[4]利用主轴倾角和不平衡率的研究来调整最大惯性力。王秋晓等[5]通过分析偏转角度来研究不平衡率和一阶、二阶惯性力。Pont等[6]探讨了曲轴质量偏心角对曲轴稳定性的影响和偏移对压缩机行为的影响，闵剑青等[7]对曲轴质心的位置对惯性力平衡的影响进行研究。

很多学者运用多体动力学软件Adams来研究曲柄连杆机构。吴迪等[8]和王金友等[9]通过该软件建立了曲柄连杆机构的动力学仿真模型，分析曲柄连杆机构的运行情况。张小明等[10]和张冬香等[11]运用Adams软件得到惯性力与平衡重参数的变化曲线，通过优化平衡重的参数，可以减小干扰力，实现惯性力的平衡。蒋立军[12]运用该软件研究了偏心距和曲柄连杆机构产生的干扰力和力矩的关系，表明改变偏心距可以减小往复惯性力。夏江敏等[13]对曲柄连杆机构进行振动分析，得到加速度频率响应曲线。这些研究运用多体动力学软件，通过对影响参数的优化，减小了惯性力。

上述研究以减少曲柄连杆机构受到的惯性力为目的来调整机构和优化参数，但这些参数对压缩机振动的影响尚未有进一步研究。本研究以某型号压缩机为研究对象，运用理论分析和多体动力学仿真方法，研究曲柄连杆结构参数对压缩机振动的影响。实验验证了优化后的参数能够降低压缩机的振动。

1 偏心式曲柄连杆机构惯性力理论分析

某型号压缩机为单缸卧式压缩机，其曲柄连杆机构的主轴为直立布置，采用偏心轴形式，气体只在活塞一侧进行压缩，简化后的物理模型[14]如图1所示。

图1 曲柄连杆机构动力学模型Fig.1 Dynamic model of crank-connecting rod mechanism

设曲柄OA绕曲轴中心线O以角速度ω作逆时针转动，曲柄半径OB=r，连杆长L，曲轴偏置e，平衡块的质心到曲轴中心线O的距离为ρ，连杆与气缸中心线的夹角为连杆摆动角β，曲柄转角α。

设曲柄连杆机构旋转质量为mr，其包括连杆大头等效质量和曲轴销质量，旋转惯性力Fr，质径积为Pr=mrr；往复质量为mj，其包括连杆小头等效质量、活塞销质量和活塞质量，一阶往复惯性力Fj，质径积为Pj=mjr；平衡块的质量为mw，质径积为Pw=mwρ。

根据牛顿第二定律，在x,y轴上建立平衡方程[15-16]，有

(1)

带入质径积得

(2)

简化后得

(3)

合成后，剩余惯性力为

(4)

根据对曲柄连杆机构的受力分析，曲柄连杆机构所受的往复惯性力Fj通过连杆和曲柄传递到压缩机的主轴承座上，使压缩机产生垂向振动，而且在传递过程中，会产生倾覆力矩Mj，使压缩机产生扭转振动。

Mj=Fjtanβ(lcosβ+rcosα)=Pjω2tanβ(lcosβ+rcosα)。

(5)

压缩机的旋转惯性力Fr由曲柄传至主轴承座，使压缩机产生垂向和横向振动。因此，当压缩机运转时，这些惯性力是引起压缩机振动的根源[17-18]。减少惯性力是降低压缩机振动的重要途径，从式(4)可以看出，剩余惯性力会随着曲轴的旋转而周期性变化，所以通过改变影响参数，可以减少剩余惯性力。

2 剩余惯性力F影响因素分析

该压缩机曲柄半径r=10.3 mm，连杆长L=41 mm，曲轴偏置e=2.95 mm，旋转质径积Pr=623.665 g·mm，往复质径积Pj=474.83 g·mm，平衡块质径积Pw=906.93 g·mm。考虑到压缩机的空间尺寸，从式(4)可以看出，在影响剩余惯性力的参数中，曲轴和连杆的尺寸难以改变，因此对平衡块质径积Pw和曲轴偏置e进行分析。

2.1 剩余惯性力F与平衡块质径积Pw的关系

根据式(1)分析可得，平衡块能够完全平衡旋转惯性力和部分往复惯性力，所以平衡块的质径积在旋转惯性质径积与旋转、往复质径积的和之间，即Pw在Pr到Pr+Pj之间。对Pw进行赋值，在Matlab软件上进行分析[19]，得到剩余惯性力F和Pw的关系，如图2所示。

由图2可以看出，给定平衡块的参数后，剩余惯性力随着曲轴转角的变化呈正弦曲线变化。但是，当Pw取值范围在750～950 g·mm时，剩余惯性力变化较小。因此在这一区间，可以通过仿真分析，取得Pw最优值。

2.2 剩余惯性力F与曲轴偏置e的关系

该型号压缩机的曲轴回转中心线与气缸中心线不相交，因此为偏心曲柄连杆机构。根据偏心方向不同，分为正偏心机构和负偏心机构。该压缩机采用正偏心机构，在活塞下行时连杆摆角较小，使得做功行程中活塞侧推力有所减小。

根据式(1)，对曲轴偏置e进行赋值，运用Matlab软件进行数值计算，得到剩余惯性力和曲轴偏置e的关系，如图3所示。

图2 剩余惯性力F与Pw的关系Fig.2 Relationship between residual inertial forceFandPw

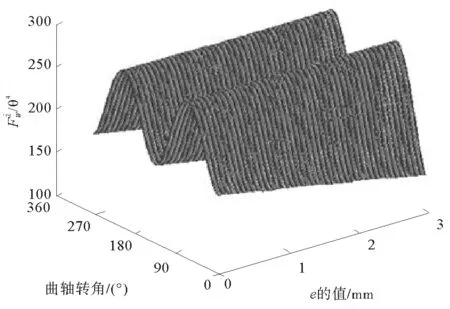
图3 剩余惯性力F与e的关系Fig.3 Relationship between residual inertia forceFande

从图3中可以看出，给定曲轴偏置的数值后，剩余惯性力随着曲轴转角的变化呈正弦曲线，在曲轴偏置数值缓慢增大过程中，正弦曲线的峰值也在逐渐增大，即剩余惯性力也随之增大。

图4 压缩机三维实体模型Fig.4 3D solid model of compressor

3 仿真分析

3.1 模型建立

利用Pro/Engineer三维造型软件建立压缩机实体三维模型[20]，将模型导入到ADAMS/VIEW中。底座的弹簧与大地连接，曲轴与电机同步转动，添加固定副，平衡块用固定副安装在曲轴上，曲轴和连杆大头用点-线副连接，连杆大头和活塞销以及活塞销和活塞的连接处添加旋转副，活塞和气缸之间用滑移副连接[21]，仿真模型如图4所示。

对压缩机多体动力学模型进行仿真，在活塞运动一侧添加一个最大振幅为10，相位角为0，水平方向的正弦激振力作为输入。在压缩机底部电机与外界连接的4个弹簧处添加4个垂直方向的输出通道，通过4个输出通道的频率响应，分析剩余惯性力参数对压缩机振动的影响。

3.2 平衡块质径积Pw参数分析

对压缩机的平衡块质径积参数的理论分析可知，当Pw在750～950 g·mm之间取值时，剩余惯性力变化较小。因此，对Pw间隔10 g·mm进行取值，分别进行振动仿真分析，得到压缩机内部的振动传递到壳体的频率响应。图5为Pw影响的加速度幅频响应曲线。

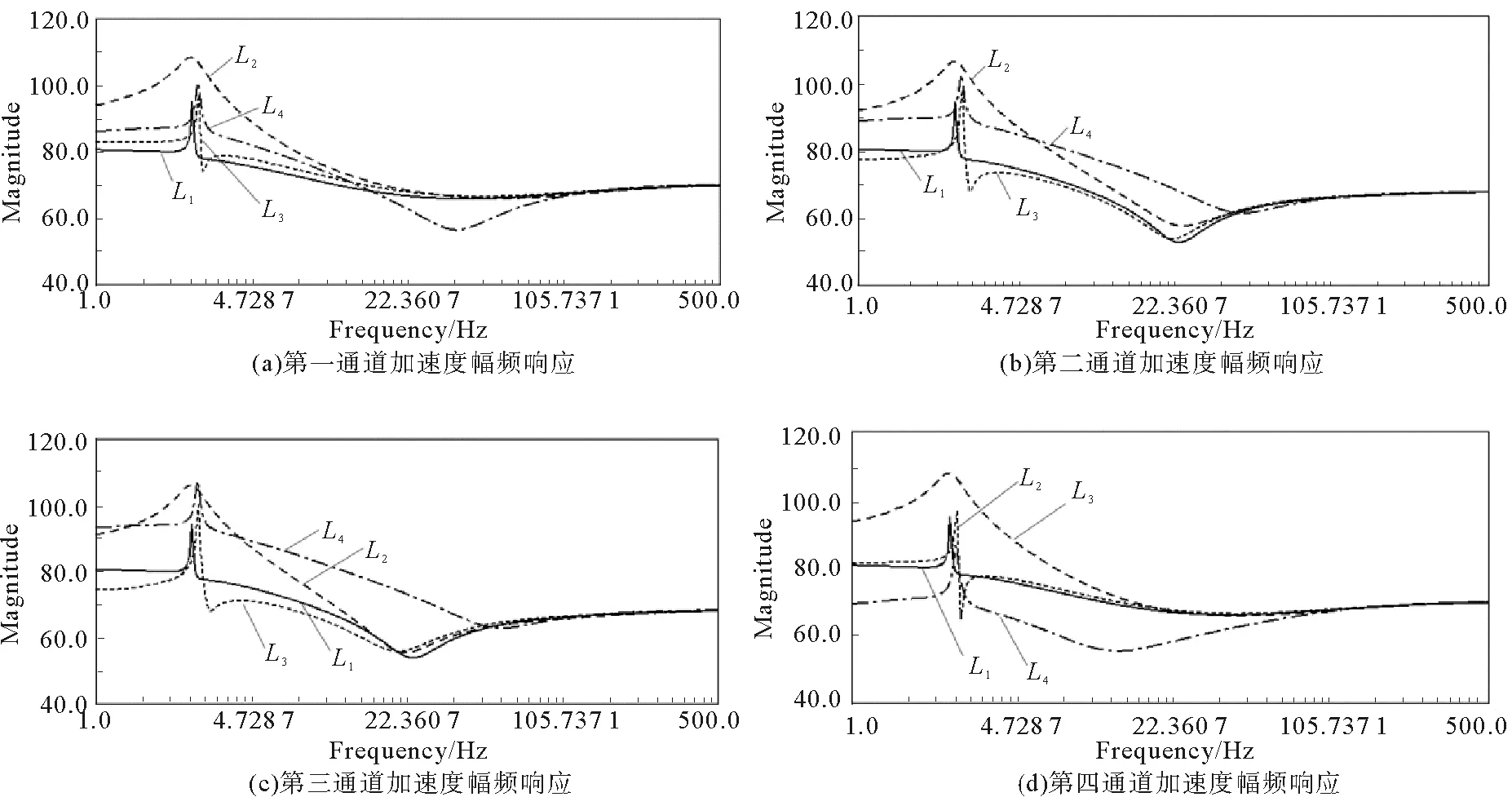
图5 Pw影响的加速度幅频响应曲线Fig.5 Acceleration amplitude-frequency response curve affected byPw

图5每个通道加速度幅频曲线的4条曲线分别是:当平衡块质径积Pw的取值为当前参数906 g·mm时，频率响应的曲线为l1;当Pw的取值为740、770、790、870和940 g·mm时，频率响应的曲线均为l2；当Pw的取值为760、780、820、840、860、920和930 g·mm，频率响应的曲线均为l3；当取Pw其余值时，频率响应的曲线为l4。

从图5可以看出，平衡块质径积Pw对压缩机的振动产生较大影响，改变平衡块质径积参数可以改变压缩机的加速度频率响应。当平衡块质径积为曲线l3代表的参数时，在第二和第三通道比原有参数产生的加速度幅值有明显降低。但在Pw取值范围750～950 g·mm中，有些参数取值可以减小剩余惯性力，但压缩机的振动并未降低。因此，通过振动仿真分析，优化平衡块质径积参数，可以更有效地降低压缩机振动。

3.3 曲轴偏置e参数分析

通过对压缩机实际测量，得到曲轴偏置为2.95 mm。为分析曲轴偏置对振动的影响，在0～3.5 mm选取7个参数，e1=0.45 mm，e2=0.95 mm，e3=1.45 mm，e4=1.95 mm，e5=2.45 mm，e6=2.95 mm，e7=3.45 mm，分别对每个参数进行振动仿真分析。压缩机底部的加速度幅频响应曲线如图6所示。

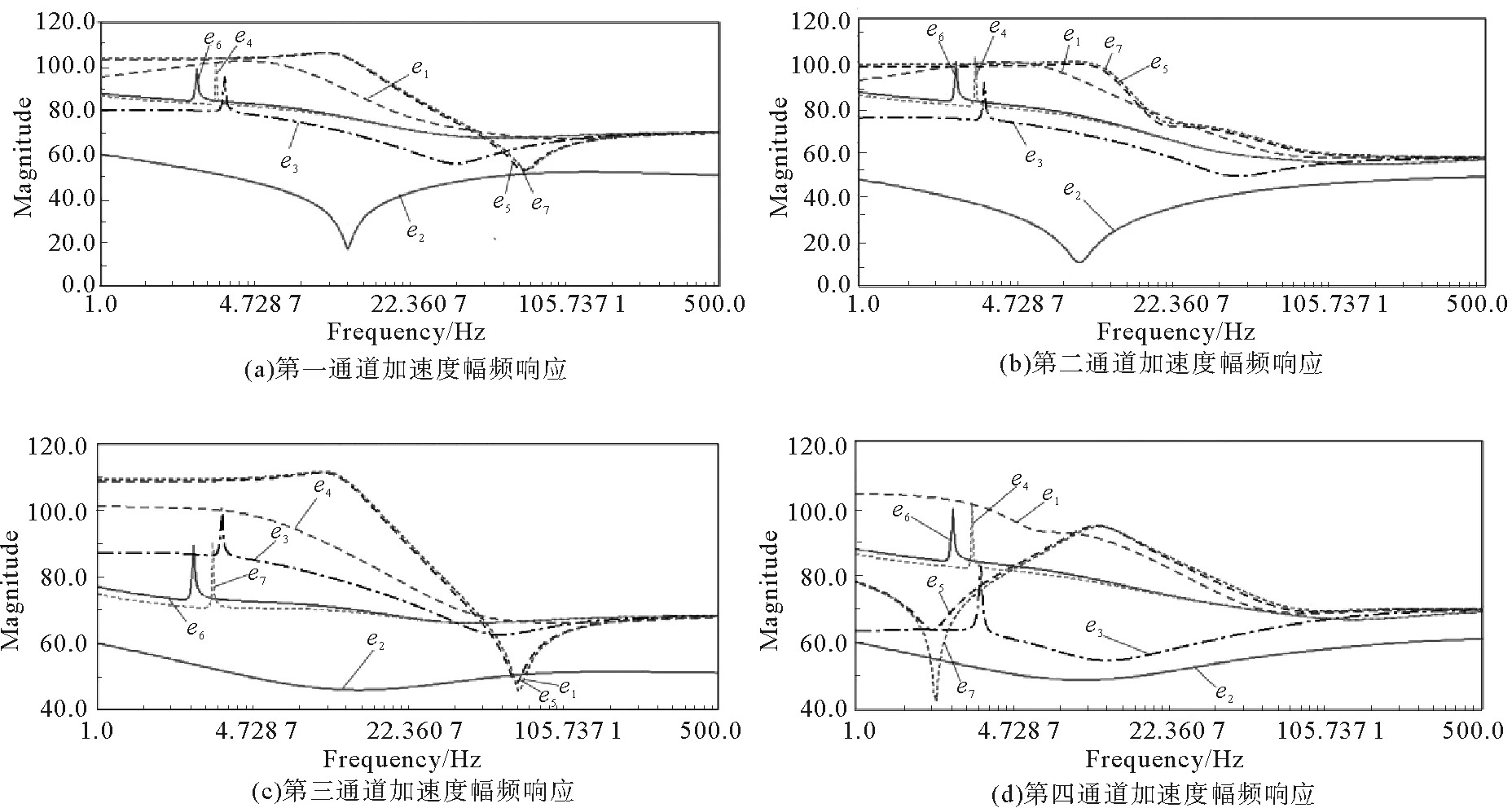
图6 曲轴偏置e影响的加速度幅频响应曲线Fig.6 Acceleration amplitude-frequency response curve affected by crankshaft offsete

从图6中可以看出，曲轴偏置对压缩机的振动影响较大。当曲轴偏置为e2时，加速度幅值最小。当曲轴偏置为e4时，压缩机的加速度幅值与原偏置e6接近相同。当曲轴偏置为e3时，除在第3个通道产生的加速度比原来的偏置稍大外，在其他输出通道，加速度幅值均有较大幅度降低。当曲轴偏置1.95和1.45 mm时，加速度幅值可以降至50 dB，在第一通道降到20 dB，有效减小了压缩机的振动。

4 实验分析

为验证仿真结果，在半消声室内对压缩机振动进行测试，如图7所示。进气阀口、排气阀口分别与进气管道、出气管道连接，3个加速度传感器分别放置在压缩机的X、Y和Z轴，压缩机正常运转，测量压缩机壳体的振动。

图8(a)为平衡块质径积对压缩机振动影响的加速度幅频响应曲线，L1为3.2中仿真优化后的平衡块质径积参数，L2为压缩机原有平衡块质径积参数。图8(b)为曲轴偏置对压缩机振动影响的幅频响应曲线，e1为3.3中仿真优化后的曲轴偏置参数，e2为压缩机原有的曲轴偏置参数。

图7 压缩机壳体振动实验Fig.7 Compressor shell vibration experiment

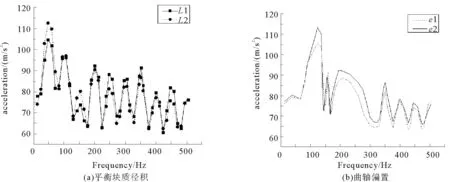
图8 实验测得加速度幅频响应曲线Fig.8 Experimentally measured acceleration amplitude-frequency response curve

从图8(a)可以看出，优化后的幅频响应曲线更趋平缓，加速度幅值降低。在频率为50 Hz时，加速度幅值由112 dB减小为105 dB。从图8(b)可以看出，曲轴偏置经优化后，加速度幅值明显降低，平均降幅约为5 dB。

5 结论

本研究采用多体动力学仿真和实验相结合的方法，以减小压缩机振动加速度幅频响应为目标，对压缩机曲柄连杆机构的平衡块质径积和曲轴偏置参数进行了分析。与单纯依靠减小不平衡惯性力来降低压缩机振动噪声的传统方法相比，该方法通过优化曲柄连杆机构的结构参数，能够更加有效地降低压缩机的振动与噪声，实验结果验证了该方法的可行性。该方法为冰箱压缩机曲柄连杆结构的参数设计，降低压缩机的振动噪声，提供了可行性的途径。