面向报警根源分析的历史相似数据段查找

(山东科技大学 电气与自动化工程学院，山东 青岛 266590)

报警系统对于工业生产的安全性、高效性和有序性起着至关重要的作用[1-2]。工业报警系统的主要功能是帮助现场操作员监测工业运行的状态，当设备运行异常时产生报警，现场操作员需要分析报警根源，并采取相应的措施消除报警。工业报警系统的研究已经受到业界和学术界越来越多的关注[3-6]。

报警根源分析是工业报警系统的一个重要课题。Wen等[7]和Chang等[8]通过建立描述异常情况与报警变量之间关系的先验知识，进而分析报警原因，提出的算法需要进行复杂的数学运算，适用于复杂的报警处理问题。Dashlstrand[9]和Souza等[10]分别通过使用多级流模型或模糊神经网络进行报警根源分析，多级流模型使得数据建模工作相对容易，模糊神经网络使得系统故障的定位有较强的容错性，但给出的算法过度依赖专家经验。Simeu-Abazi等[11]利用动态故障树来定位报警中的故障，该算法可以过滤掉大量的误报警，提高报警诊断效率，但是其中所用到的参数难以确定。Guo等[12]基于原因假设和报警之间的时间约束网络确定故障原因，并确定误报警和漏报警原因。Wee等[13]从数据中得到贝叶斯信念网络和模糊认知图，以推断出报警的根本原因，消除了寻找领域专家困难、专家意见不一致以及知识学习过程中的人为错误等问题，但该方法需要丰富的数据才能有效地工作。雅斯太等[14]建立因果网络模型，提出了一套基于可调参考范围传递熵的报警根源分析方案，所设计的算法优化了传统的传递熵算法在参考变量预报范围时存在的不足，使传递熵的计算结果更加合理，但算法准确度过度依赖数据概率密度估计的精度，且需要较长的计算时间，导致无法应用于在线建模。陈忠圣等[15]结合过程的单元划分方法和变量的层次划分方法，利用概率图网络模型建立了变量间的因果关系，形成了一套基于概率图网络模型的报警根源识别方法，虽然考虑了变量之间的相关性，但是在确定因果关系网络模型时没有包含异常操作下的数据，导致模型并不完善。马小梅等[16]通过改进布谷鸟算法并应用于贝叶斯网络结构学习中，结合偏相关性分析及贝叶斯网络推理进行报警根源分析，改进之后的算法与传统算法相比具有收敛速度快、精度高的特点，但是该算法不适用于更大规模的网络结构。本研究所提出的算法从多个变量之间的物理关系出发，通过对传统相关系数算法的优化，能更快速地帮助操作员进行报警根源分析，贴合实际工业应用。

由于历史数据段的时间跨度大，记录的数据量大，可以帮助现场操作员根据已出现过的异常历史数据进行异常状况分析，本研究通过在历史数据中查找与当前异常数据相似的数据段，帮助操作员进行报警根源分析。本研究在文献[17]描述的Distance Profile基础上，改进了其中的单变量相似数据段查找算法，消除了其在计算样本间距离时存在的误差；提出一种新的基于距离分布的时间窗口确定方法；形成一套多变量相似数据段查找的方法，最终提出一种新的报警根源分析方法。

1 问题描述

2 相似数据段查找方法

2.1 单变量的相似数据段查找

文献[17]中的计算距离公式为：

(1)

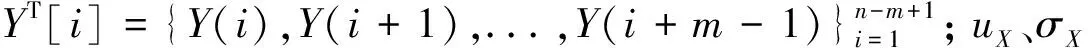
(2)

对于两段完全相同的数据段，相关系数应为1，距离应为0。综合公式(1)和(2)得到计算距离

(3)

其中，XY[i]是X和Y[i]的卷积。本研究采用快速傅里叶变换的方法来计算卷积XY[i]。卷积定理可以简化卷积的运算量，利用傅里叶变换的快速算法之后，总的计算复杂度为O(nlogn)。由公式(3)计算出两段完全相同数据段的距离值为0，表明公式(1)存在的误差被消除，因此本研究将公式(3)作为计算距离的公式。

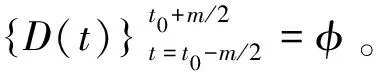
2.2 时间窗口m的确定

历史相似数据段查找的目标是在历史数据中找到相似度较高的相似数据段，体现在距离矩阵上就是得到较多的较小值(接近于0)，如图1圆点所示。

图1 窗口宽度合适的距离分布图Fig.1 Distance distribution map with appropriate window width

若给定数据段的时间窗口宽度过小，会找到很多相似数据段，但是这些相似数据段几乎不包含数据特征，对于报警根源分析没有意义。若给定数据段的时间窗口宽度过大，则几乎找不到相似数据段，即查找结果距离均值较大，相似度很低。因此，确定合适的时间窗口宽度非常重要。

由于不同的窗口宽度m可以确定不同的距离矩阵D(m)，取D(m)的局部极小值的平均值作为求解窗口宽度的指标，指标最小时的窗口宽度就是合适的。若两个窗口的指标相等，则取较大的窗口宽度。如公式(4)所示：

(4)

输入:窗口宽度m输出:窗口宽度指标Fmin[D(m)]n1 将m代入公式(3),得到距离向量D(m)2 找到D(m)的所有极小值并从小到大排序,得到向量fmin[D(m)]3 为fmin[D(m)]中的元素找到在D(m)中对应的位置,形成位置向量Q4 fori←1tolength(Q)do5 j←Q(i)6 删除Q中位于(j-m/2,j+m/2)且不等于j的元素7 更新length(Q)8 ifi=length(Q)9 then break10 end if11 end for 12 得到排序后的D(m)的局部极小值,形成Fmin[D(m)]13 根据用户需求确定n,取D(m)中最小的n个局部极小值的均值,得到Fmin[D(m)]n

2.3 多变量的相似数据段查找

在实际工业生产中往往存在较多的相关变量，因此本节在单变量相似数据段查找的基础上，将算法扩展到多变量的情况。通过公式(3)已得到每一个单变量的距离矩阵

其中i=1,2,…,I，I为变量个数。将每一个变量的距离矩阵Di标准化到同一范围[0,2]，然后相加得到所有变量总的距离矩阵

(5)

其中：Wi为各变量所占权重，该权重值可由用户确定；I为变量个数。D中就包含所有变量综合之后的距离，距离越小，这些变量的综合相似度就越高。相似度S与距离之间的关系为：

(6)

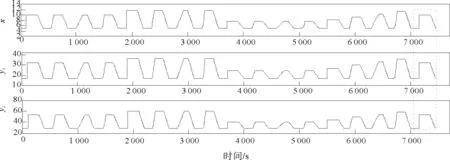
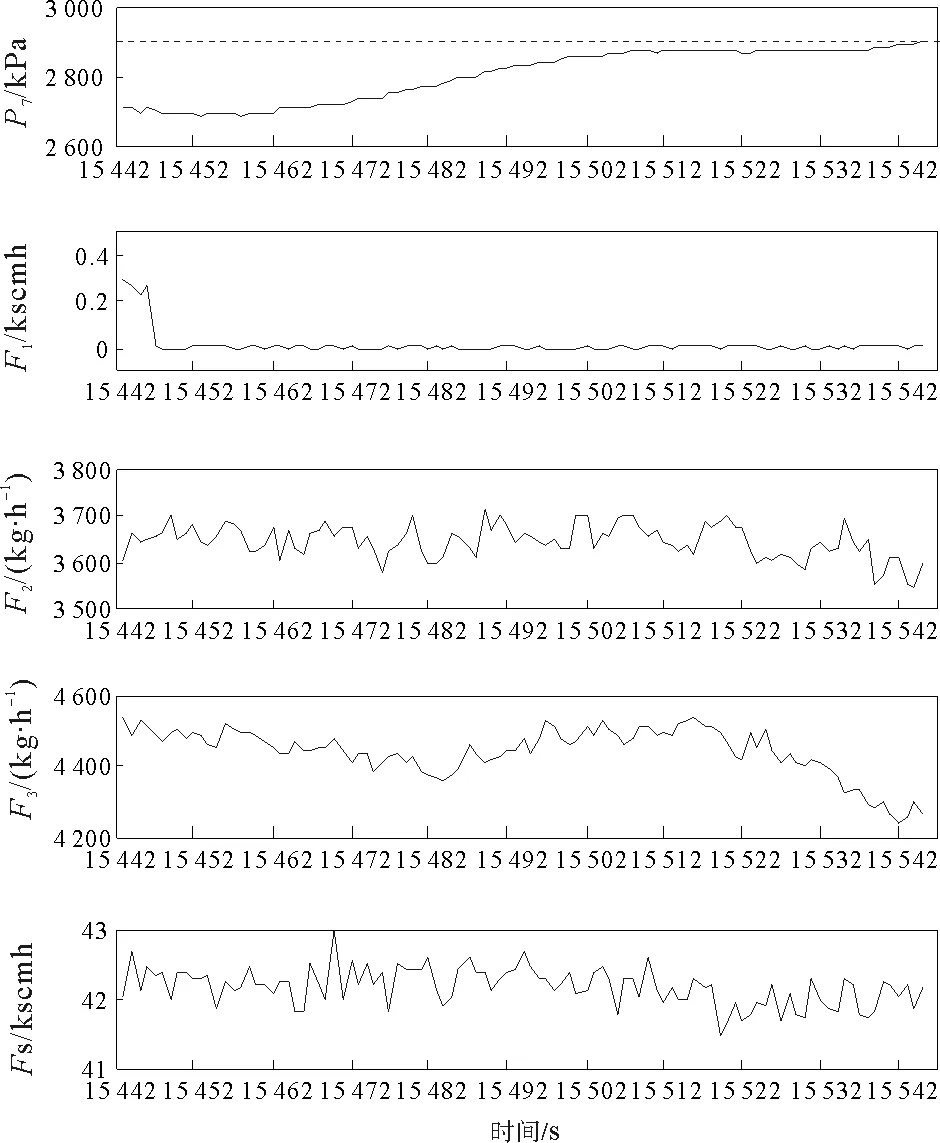
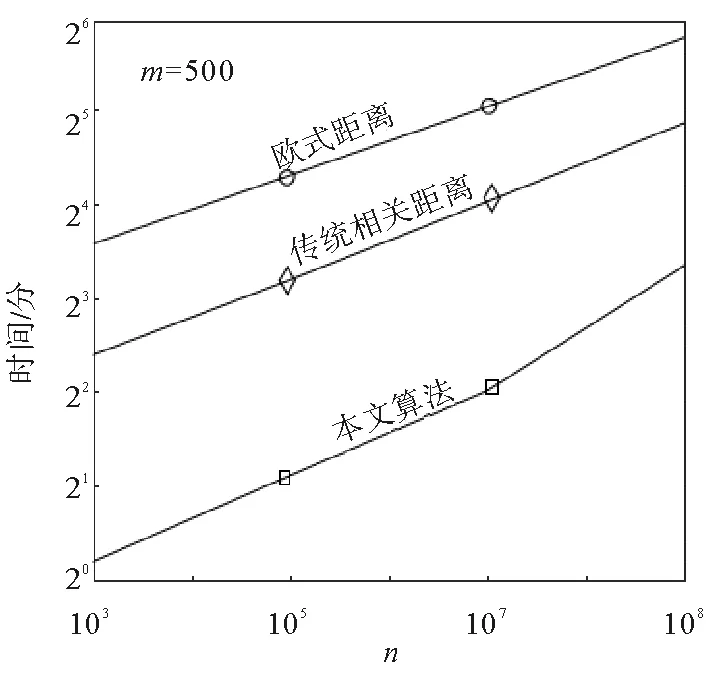
其中I为变量个数。若D中元素出现距离相等即D[i]=D[j]的情况，则进一步比较主变量距离D1[i]与D1[j]的大小，若D1[i]

综上，进行多变量相似数据段查找的步骤为：

1) 通过公式(4)确定合适的时间窗口宽度m，即确定要查找的数据段X；

2) 由公式(3)计算出每一个变量的距离矩阵Di；

3) 通过公式(5)得到所有变量的总距离矩阵D;

4) 去除矩阵D中的“灰色区域”，具体过程的伪代码为：

输入:总距离向量D输出:相似数据段所在的位置向量Q 1 对D从小到大进行排序,得到向量D′2 为D′中的元素找到在D中对应的位置,形成为位置向量Q3 fori←1tolength(Q)do4 j←Q(i)5 删除Q中位于(j-m/2,j+m/2)且不等于j的元素6 更新length(Q)7 ifi=length(Q)8 then break9 end if10 end for

5)Q中的元素值即为相似数据段在原数据中的位置。

3 仿真案例

本节通过数据仿真和TE过程验证所提方法的有效性。

3.1 数据仿真

构造多变量数据过程如下：首先构造一组数据x=[x1,x2,…,xn]，将其代入

y1=3x+[2,2,…,2]
y2=5x+[3,2,…,3]

得到相关变量的仿真数据如图2所示。

图2 三个相关变量的仿真数据Fig.2 Simulation data of three related variables

通过步骤1)确定时间窗口宽度，取n=16，m∈[300,600]，得到指标分布如图3，可见在m=403时指标值最小，即取窗口宽度为403。通过步骤2)～5)得到相似数据段查找的结果如图4所示。图4中虚线框内为当前时刻要查找的数据段(与标号1数据段相同)，长度为403。数字标出了16段相似数据段并对相似程度进行了排序。相似度前16段数据的距离D以及经过公式(6)得到的相似度S分别为：

图3 窗口指标图Fig.3 Window index map

图4中标号1、2、3、4的数据段与被查找的数据段形状完全相同，但幅值不同，标号5～16的数据段与被查找的数据段形状相似，但幅值不完全相同，并且幅值也不同。本文相似数据段查找的算法是计算两段数据段的线性相关距离，所以标号1、2、3、4的数据段与被查找的数据段的距离应为0，相似度应为1，剩下的数据段与被查找的数据段的距离应逐渐增大，相似度逐渐降低。综上，仿真结果与真实结果一致。

图4 多变量相似数据段查找的仿真结果Fig.4 Simulation results of multivariate similar data segment search

3.2 TE过程

TE过程是一个实际化工过程的仿真模拟，主要由4种气态物料A、C、D和E参与反应，生产出2种产品G和H，并伴有1种副产品F，此外在产品的进料中含有少量的惰性气体B。整个过程主要由4种反应组成，反应方程式为[18]：

A(g)+C(g)+D(g)→G(l)
A(g)+C(g)+E(g)→H(l)
A(g)+E(g)→F(l)
3D(g)→2F(l)

TE过程由搅拌反应器、冷凝器、产物分离器、汽提塔和压缩机5个主要设备所组成，每个设备完成不同的工作。TE过程中有22个过程变量，同时，TE过程模型还预设21种扰动来体现系统发生的不同故障。

选取搅拌反应器部分的5个相关过程变量进行试验，即物料A的流量(F1)、物料D的流量(F2)、物料E的流量(F3)、反应器进料的流量(F6)、搅拌反应器的压力(P7)以及设定d6故障(物料A流量发生损耗)。共取15 544个采样点，采样间隔为1 s，其中设置了3次故障，第三次故障导致当前时刻的报警。这里对搅拌反应器的压力进行监测，报警线为2 895 kPa。TE过程数据如图5所示。

图5 TE过程数据Fig.5 TE process data

首先通过步骤1)确定时间窗口宽度，取n=2，m∈[50,300]，通过公式(4)得到m=103。图6为当前数据段(被查找数据段)，然后通过步骤2)～5)得到相似数据段查找的结果(如图7)。

图6 当前数据段Fig.6 Current data segment

图7 相似数据段查找结果Fig.7 Similar data segment search results

图8 3种算法的计算速度对比Fig.8 Comparison of calculationspeeds of three algorithms

图7(a)为找到的相似度第一的数据段，相似度为94.37%，7(b)为找到的相似度第二的数据段，相似度为89.97%，横坐标为三段数据分别在历史数据中的位置。已知在历史中图7(a)(b)发生报警的原因，通过操作员的对比分析，可以准确得到当前数据段的报警根源。

图8将本算法与采用欧氏距离、传统相关系数算法进行相似数据段查找速度对比，可见本算法不仅可以准确地找到当前数据的相似数据段，而且大幅度提高了计算速度。图8中n代表时间序列长度，m代表时间窗口宽度，可以看到在窗口宽度为500且时间序列足够长时，本算法可以大大提高计算速度，更快地帮助操作员进行报警根源分析。

4 结论

本研究改进了一种单变量相似数据段查找的算法，消除其在计算样本距离时存在的误差，然后提出一种新的基于距离分布的窗口宽度确定方法，最后形成一种可以用于多变量相似数据段查找的方法，并对数据段的相似程度进行排序。通过该方法可以找到当前报警变量及其相关变量的历史相似数据段，以辅助操作员进行报警根源分析。最后，通过数据仿真和TE过程验证了本方法的有效性。