三次均匀B样条在求解轨道曲率中的应用

蔡文豪 黄 玲 高 聪

（广东省建筑科学研究院集团股份有限公司，广东 广州 510500）

随着大型城市的经济稳步增长和科技高速发展，越来越多的人口流向了这些大型城市，拥挤的人口给城市交通带了巨大的压力和挑战。城市轨道交通成为应对这一挑战的首选。城市轨道交通是特大型隐蔽性的系统工程，一项工程投资将达上百亿，涉及十几个专业，地铁施工具有难度大、复杂程度高、项目周期长，周边环境影响大、风险等级高的特点。为了充分保障城市轨道交通完成每天安全运送数百万人次的任务，其质量控制也是尤为严苛，这其中之一就是对地铁隧道的各项参数进行检测。

运营期间的地铁隧道关注重点之一在于其轨道的位移监测。地铁隧道的沉降控制值、沉降速率控制值均已在相关规范中作出规定。为了保障列车行驶安全，《上海市地铁沿线建筑施工保护地铁技术管理暂行规定》规定了地铁轨道的最小曲率半径不得小于15 000 m，这一限值在工程界被广泛采用[1-3]。对于具体的隧道区间，通常只按照指定的间隔监测其沉降值，如何根据这一系列离散的沉降监测值求整个隧道的曲率值是一个重要的问题。文章将采用三次均匀B样条曲线拟合的方法进行求解。

1 三次均匀B样条

在数值分析领域中，B样条或基本样条是这样的样条函数——其对给定的自由度、平滑度和域区划分具有最小的支集（support）。给定自由度的任何样条函数都可以表示为该自由度的B样条的线性组合[4]。基本B样条具有彼此等距的结点，可很好地应用于曲线拟合和数值差分中。

本质上，n阶样条是一个变量为x的n-1阶分段多项式函数。各分段多项式“接头”处的变量值称之为节点，用…,t0, t1, t2, …表示，并且将这些节点在数值上按照非递减顺序排列。若上述节点各异时，多项式部分的前n-1个导数在每个节点连续；若上述节点中有个节点重合，则只有样条的前n-r个导数在该节点连续。此外，若上述节点各异并且等间距，称之为均匀样条，否则称之为非均匀样条。本研究是基于均匀样条展开的。

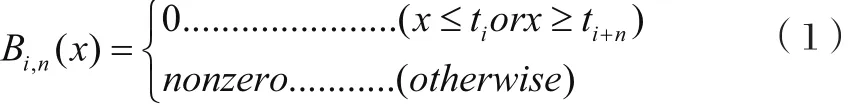
或者，可以通过Cox-de Boor递归公式[5]来构造B样条。对于给定的结点序列…, t0, t1, t2, …，一阶B样条可以如此定义：

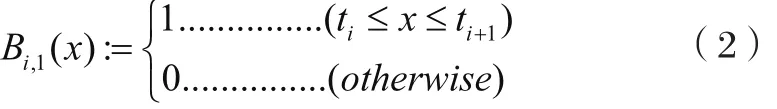
而更高阶的B样条通过如下递归公式定义：

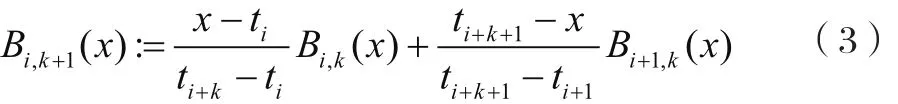
2 曲率的求解

按照上述方式可根据原始监测数据进行三次均匀B样条拟合，从而求出整个隧道区间的沉降曲线，理论上，该曲线是一条二阶连续可导的平滑曲线。由于计算过程均采用计算机编程的方式完成，实际上最终的曲线由一系列间距很小的离散点表示。沉降后的轨道曲率正是基于这一系列离散的光滑散点，并采用数值计算的方式完成。笔者将介绍在曲率求解中遇到的问题，以启发读者。

曲线的曲率（curvature）就是针对曲线上某个点的切线方向角对弧长的转动率，通过微分来定义，表明曲线偏离直线的程度（如图1所示），数学上表明曲线在某一点的弯曲程度的数值[6]。曲率的另一个定义是，在曲线任一点作一个与该曲线相切的圆（密切圆），该圆半径的倒数即为该曲线在该点的曲率，而该圆的半径则称之为该点处的曲率半径，如图2所示。

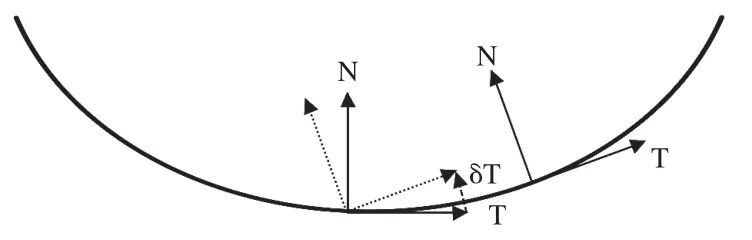
图1 曲率的数学定义

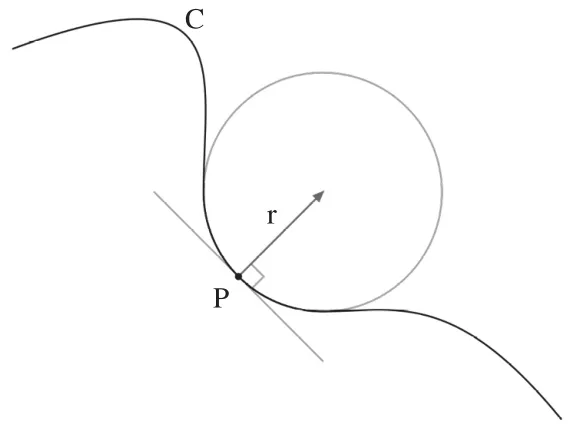
图2 曲率与密切圆的关系

对于曲率的求解，最先想到的就是定义法。即对于任何一个光滑曲线 y=f(x)，其曲率可根据定义推导出如下公式：

上式中关于一阶导数和二阶导数的求解，可以对曲线横坐标做尽可能小的细分，并采用差分近似微分的方法（即在图像上表现出割线近似代替切线的方法）来进行数值计算。即第j点的一阶导数可由如下差分格式求得：

课堂1：老师声音清晰，但是紧张，后稍好。准备教学材料充分，讲故事学习单词，较好，但是节奏缓慢。问题太难，提示较少，没有介绍强调具体的事例或语言点，给学生做笔记。(2006年10月9日)

通常，在计算过程中取均匀步长，即h=x( j)-x( j-1)为一定值，则上式为：

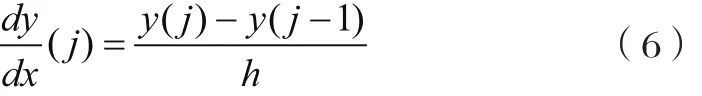
同理，即第j点的二阶导数可由如下差分格式求得：

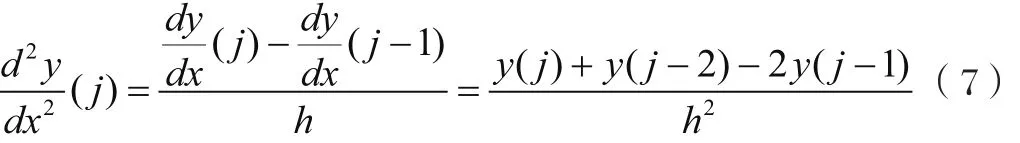
需要注意的是，对于讨论的轨道曲率半径的求解问题，由于所讨论区间隧道的长度方向量级通常都在数十米至数百米之间，而隧道的沉降都是毫米量级，因此上述差分数值都非常小，再加之差分格式稳定性问题[7]，导致用曲率公式方法求解轨道曲率的结果很不理想，极易出现数值震荡、发散、无法计算结果等问题。因此，对于轨道曲率的求解需要另辟蹊径。

根据隧道沉降量相对于长度方向极小的特点以及数值计算过程对里程区间纵向充分划分的前提条件，可采用三点定圆法近似求解轨道曲率[8]。其求解过程如下。

对于轨道曲线上的任意三点A，B，C，总能确定一个外接圆（若这三点在一条直线上，则可认为该外接圆半径无穷大），若这三点无限接近，则该外接圆与轨道曲线相切，此时外接圆的半径的倒数即为曲线在该点的曲率，如图3所示。正如前文所述，轨道沉降量相对于轨道纵向方向极小，且里程区间纵向充分划分，即A，B，C三点充分接近彼此。这时可由A，B，C三点确定的外接圆来近似替代曲线的密切圆，换言之，该圆的半径倒数即为要求的曲率。

图3 三点定圆法求取率示意图

上述三角形ABC的三边长度分别为BC=a，CA=b，AB=c则根据正弦公式很容易推出三角形外接圆半径的表达式，其倒数即为曲率：

注意到在求解轨道曲率过程中，上述三角形ABC实际上是一个“极狭长”的钝角三角形，换言之，a+c-b≈0，甚至对于平直的轨道段有a+c-b=0。因此，曲率的求解变成了一个如何求“极狭长”的钝角三角形面积的问题。

思路一：海伦公式法。记三角形的半周长为p=(a+b+c)/2，则三角形面积公式为：

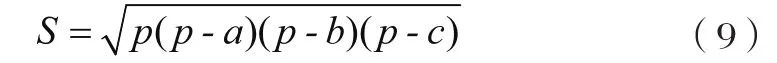
思路二：行列式法。设A，B，C三点的坐标分别为(x1,y1)，(x2, y2)，(x3, y3)，则三角形面积可由顶点坐标表示的行列式求得（式中双竖线表示行列式求绝对值）：

由于海伦公式中p-b≈0，为了避免计算中出现“大数吃小数”的数值现象，因此用三顶点的坐标建立行列式的方法求“极狭长”的钝角三角形的面积。

综上所述，一共提出了三种求解曲率的方法。由于轨道沉降值相对于其纵向里程量级特别小这一特殊原因，为了避免数值计算过程中的“大数吃小数”和其他数值发散现象，采用了三点定圆法结合坐标顶点行列式求三角形面积方法求解轨道曲率。这种做法的最主要优点是在数值计算过程中避免开根号的计算，从而有效避免数值发散。

3 应用

案例一：某地铁线路的某一区间为明挖段，隧道主要位于强风化泥质粉砂岩、中风化泥质粉砂岩、微风化泥质粉砂岩中。该区间位于珠江三角洲中西部，地形平坦，勘察期间测得钻孔地下水位埋深一般0.7～2.9 m，地下水受季节暴雨和河水水位的影响。该区间左线约3.26 km，监测点间距约40 m；右线约2.34 km，监测点间距约60 m。其最后一次沉降监测值如图4中散点所示，根据散点进行三次均匀B样条拟合得到整个区间的沉降曲线，如图4中实线所示。

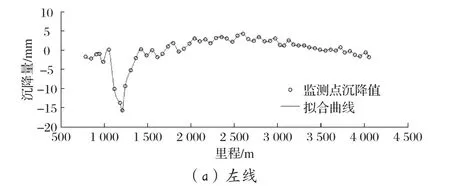
图4 案例一的监测点沉降值和拟合曲线

采用前文所述的三点定圆法结合坐标顶点行列式求三角形面积方法求解轨道曲率，如图5所示。注意，为了清晰反映轨道沉降变形后的性质，应用实例中求解“极狭长”的钝角三角形面积时并未取绝对值，导致曲率值有正有负。其中正值表示曲线是凹函数，即轨道在该微段下凹；负值则表示曲线是凸函数，即轨道在该微段上凸。下同。由图可见，轨道的曲率均不超过6.67×10-5m-1，即轨道半径均不小于15 000 m。由此表明该隧道的曲率满足安全要求。

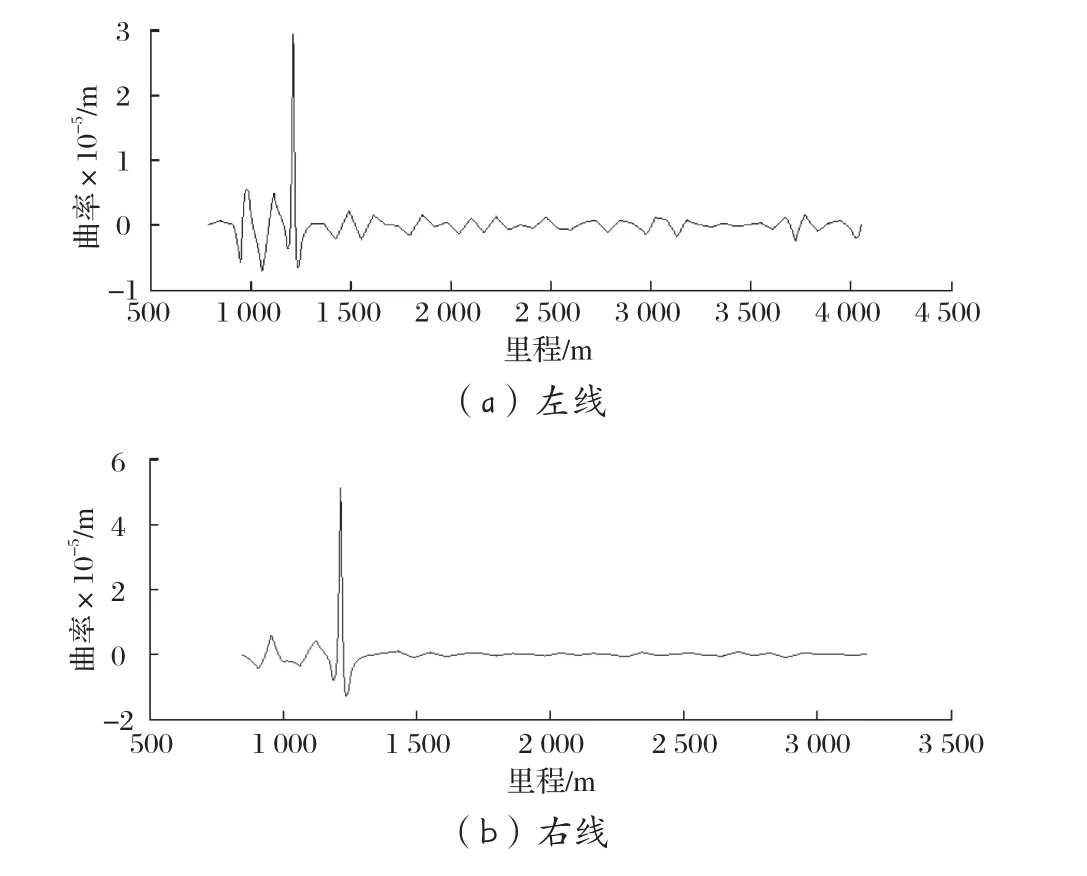
图5 案例一的轨道曲率

案例二：某地铁线路的某一区间为盾构段，地势平坦，地面建筑物众多，洞身通过段岩性主要为全、强风化花岗岩和硬塑状花岗岩残积土，洞顶主要为全风化花岗岩和硬塑状花岗岩残积土，未见断裂，岩土富水性弱。该区间左、右线均约3.6 km，监测点间距均约30 m。其最后一次沉降监测值如图6中散点所示，根据散点进行三次均匀B样条拟合得到整个区间的沉降曲线如图6中实线所示。

采用前文所述的三点定圆法结合坐标顶点行列式求三角形面积方法求解轨道曲率，如图7所示。同理，轨道的曲率均不超过6.67×10-5m-1，表明该隧道的曲率满足安全要求。

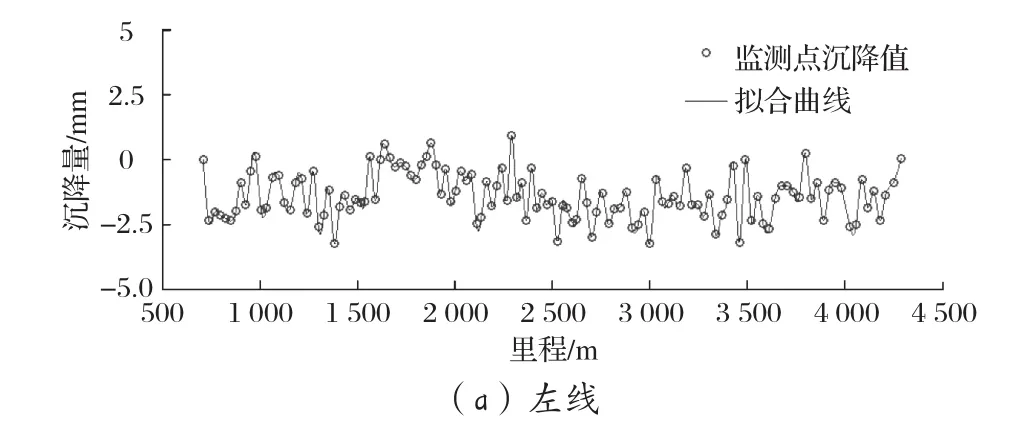
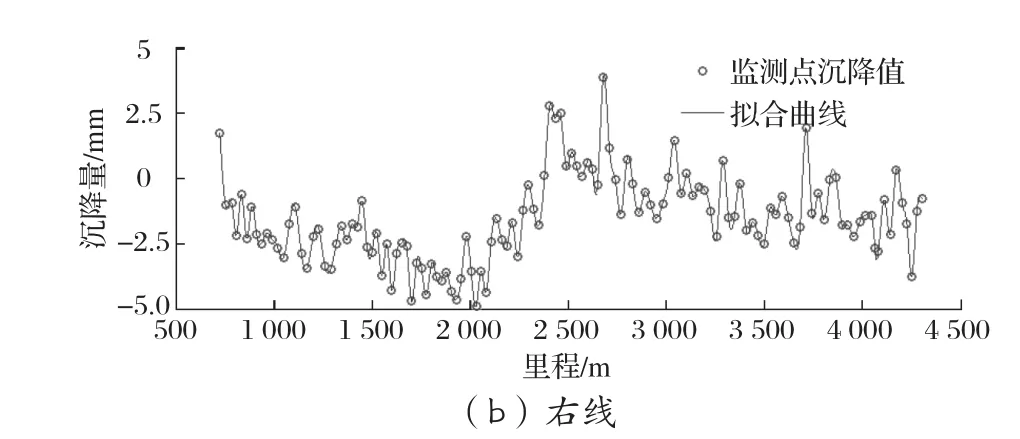
图6 案例二的监测点沉降值和拟合曲线

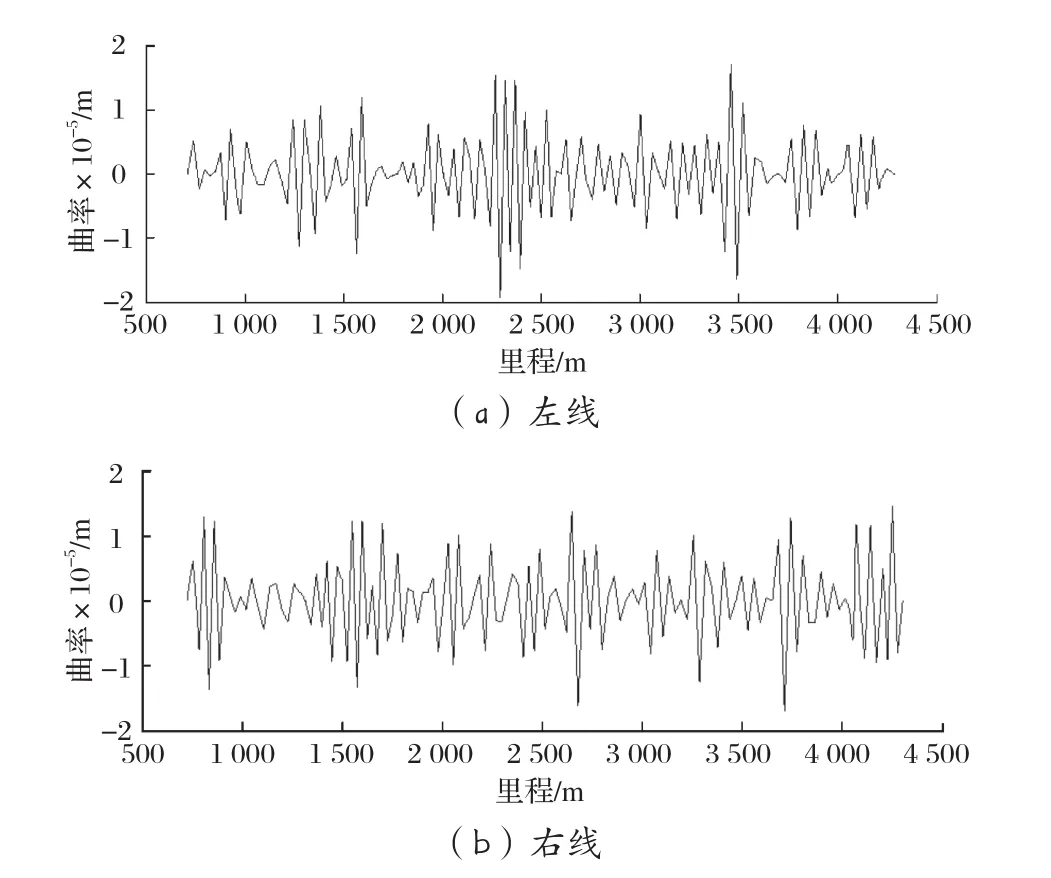
图7 案例二的轨道曲率

4 结语

文章采用的三次均匀B样条曲线拟合的方法求得的轨道曲线光滑逼真，能够真实反映发生沉降后的轨道特点。所述方法在求解轨道曲率方面具有很好的应用空间。