“对应”的观点来看动点的轨迹问题

2019-07-16湖北省武汉市梅苑中学

数学大世界 2019年11期

关键词：绕点逆时针顺时针

湖北省武汉市梅苑中学赵耀

初中阶段经常会探究一些动点的轨迹问题，很多学生不会思考，觉得找不到方法，其实，如果引导得当，学生学的得法，轨迹问题能很好地激发学生的兴趣。下面通过几个例题具体讲解。

一、直线型轨迹问题

例：如图1，已知点A 坐标为（0，2），点M（m，0）为x 轴上一动点。

（1）将点M绕点A逆时针旋转90°，得到点N，求点N 的轨迹。

（2）将点A绕点M顺时针旋转90°，得到点D，求点D 的轨迹。

两问都是轨迹问题，在函数中，自变量x 和因变量y 之间有一个固定的对应法则f，满足一一对应的关系。本题中，M 点位置如果确定，则N 点的位置也随之确定，M 和N 之间的位置也满足一一对应的关系，所以不妨用映射的观点来看本题，M 点在一条直线上运动，而对应法则f 就是M 到N 的变换关系（如图2）：绕点A 逆时针旋转90°。所以把M 看成主动点，N 点随着M 运动而运动，N 点看成从动点，主动点M 所在直线，即x 轴绕点A 逆时针转90°的直线，就是从动点N 所在的直线的轨迹。那只需要找到M 点所在直线上的一个特殊点，如原点O，绕点A 顺时针旋转90°，得到B（2，2），所以N点在经过B 点，与x 轴垂直的直线x=2 上。证明如下：如图3，作AB ⊥AO，且AB=AO，连接BN，AN，可证△AOM ≌△ABN，得∠ABN=∠AOM=90°。因为B 为定点，BN ⊥AB，所以N 点在经过点B，又与AB 垂直的直线x=2 上移动。

图3

第1 问中构造了旋转中的全等，第2 问中，由映射的观点（如图4），M 点位置确定，D 点位置也唯一确定，主动点为M 在x 轴上运动，要找从动点D 的运动轨迹，此时对应法则f 为绕点M 顺时针旋转90°，但M 点为动点，不易得出，由∠MAD=45°，，可以把对应法则f 转化为M 点绕定点A 点逆时针旋转45°，再把MA 扩大倍，到AD，就可以找到从动点D 点的位置，主动点M 所在直线，即x 轴绕点A 逆时针转45°，再以A 为位似中心，以1 ∶的比例进行位似变换的直线，就是从动点D 所在的直线的轨迹。那么可以找M 点所在直线上的一个特殊点，不妨找原点O，绕A 点逆时针旋转45°，并以A 为位似中心，位似变换得到的点C，就是从动点D 所在直线所经过的点。证明如下：如图5，在x 轴上取OC=OA，连接AC，则△OAC 为等腰直角三角形，∠OAC=45°，此时△AMD ∽△AOC，可证△AMO ∽△ADC，得到∠ACD=90°，∠OCD=45°。因为C 为定点，∠OCD=45°，所以D 点在经过点C（2，0），并与x 轴夹角为45 度的直线y=x-2 上运动。

图4

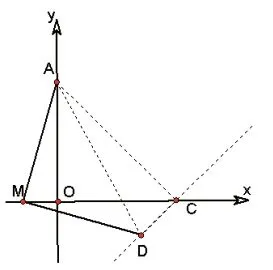
图5

二、弧形轨迹问题

例2：如图6，⊙O 中，以AB 为直径，点C 为⊙O 上一动点，以OA，AC 为边构造平行四边形ACDO，求点D 的轨迹。

图6

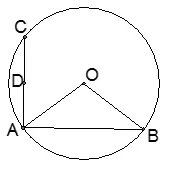
图7

图8

例3：如图7，AB 为圆O 的弦，∠AOB=120°，AB=点C 为圆O 上一动点，D 为AC 中点，当C 在圆O 上运动时，求D点轨迹。

例4：如图8，点C 是半圆AB 上一动点，以BC 为边作正方形BCDE。（1）求E 点轨迹；（2）求D 点轨迹。

图9

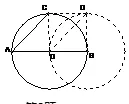
图10

例2 从映射的观点来看（如图9，图10），主动点C 到从动点D 的映射f 是向右平移AO 个单位，则主动点所在的圆也向右平移AO个单位就是从动点D 所在的圆的轨迹。例3 从映射的观点来看（如图11，图12），主动点C 到从动点D 的映射f 是以A 为位似中心的位似变换，位似比为2 ∶1，则主动点C 所在的圆的圆心O 也是以A为位似中心，位似比为2 ∶1 的位似变换，圆心为AO 的中点E，即从动点D 在以E 为圆心，DE 为半径的圆上运动。例4 第（1）问，从映射的观点来看（如图13），主动点C 到从动点E 的映射f 是绕B 点顺时针旋转90°，则主动点C 所在的半圆也绕B 点顺时针旋转90°就是从动点E 所在的圆的轨迹；第（2）问中，主动点C 到从动点D的映射f 是绕定点B 顺时针旋转45°，再扩大倍，则主动点C 所在的半圆圆心O也绕B点顺时针旋转45°，同时BO 扩大倍所到的点N，就是从动点D 所在的圆的圆心，如图14，15。