移动摄像下的目标跟踪算法*

王战，杨绍清，刘松涛，宋元

(海军大连舰艇学院，a.信息系统系；b.导弹与舰炮系；c.教保处，辽宁 大连 116018)

0 引言

运动目标跟踪是图像处理的重点和难点，在军事检测、医学研究、商业防盗等领域均有广泛应用。所谓运动目标跟踪就是在每一帧图像中找到跟踪目标的具体位置，一般可以从鲁棒性和实时性上判断跟踪算法的优劣。在跟踪目标时，不仅要考虑目标自身的复杂运动，还要考虑成像传感器在移动过程中受到外界干扰对跟踪产生的负面影响。为了保证跟踪的鲁棒性，一般在跟踪过程中加入特征匹配模块，Lowe等[1]在2000年开创性地提出了SIFT(scale invariant feature transform)局部特征匹配算法，在目标发生尺度变换和旋转缩放时还能保证良好的匹配能力，但计算量大，实时性差。2006年，Herbert Bay等[2]在SIFT算法的启发下，提出了改进算法SURF(speeded up robust features)，该算法极大地提升了SIFT算法的实时性[3]。Mean Shift算法最早由Fukunaga等[4]提出，后由Comaniciu和Meer等[5]将其用于目标跟踪，卡尔曼滤波是一种根据系统状态进行最优估计的算法。文献[6]将卡尔曼滤波和Mean Shift算法结合，保证了对快速移动目标和受到遮挡目标的跟踪鲁棒性，但在目标出现尺度变化或旋转缩放时，跟踪效果很差；文献[7]利用SURF算法与Mean Shift算法综合得到跟踪结果，该算法虽具有广泛适用性，但由于缺少预测功能，计算量大，时效性较差。文献[8]综合了卡尔曼滤波预测算法的实时性和SURF匹配算法的鲁棒性，但由于缺少迭代过程，算法的跟踪连续性较差。文献[9]将SIFT算法、卡尔曼滤波和Mean Shift组合用于跟踪，虽然在多数情况下都具有良好的跟踪性能，但无法跟踪移动摄像下的运动目标，而且SIFT算法的实时性也需要进一步加强。

深入研究文献[5-8]后，本文提出一种组合二帧差分法、Mean Shift和卡尔曼滤波的跟踪算法。该算法将二帧差分作为跟踪的第一步，消除由于成像传感器移动产生的负面影响，然后利用卡尔曼滤波预测Mean Shift算法的中心，迭代后，反馈回滤波器进行误差纠正。

1 基于SURF特征点匹配的二帧差分法

1.1 SURF算法原理简介

SURF算法与SIFT算法相同，是一种局部特征点匹配方法，与其他的特征点匹配方法相比，有更好的匹配鲁棒性。文献[10]将其与Mean Shift算法组合用于车辆检测；文献[11]提出一种组合SURF,k-means和Mean Shift目标描述方法；文献[12]利用SURF算法实现了视频补偿，提升了视频的稳定性。本文将SURF算法引入到目标跟踪中，进而改善跟踪精度。

1.1.1 建立尺度空间以及特征点检测

SURF算法为了保证尺度不变性和提升运算速度，采用Hessian矩阵行列式和盒装滤波器结合的方法检测特征点。图像中某个像素点的Hessian矩阵为

(1)

则Hessian矩阵的判别式可表示为

det(H)=DxxDyy-(0.9Dxy)2，

(2)

式中：Dxy为经过Simard等[13]提出的盒装滤波器后图像在x,y方向上的二阶微分；Dxx与Dyy同理；0.9为权值，用来平衡滤波器替换所带来的误差。当det(H)>0时，该点为局部极值点。

1.1.2 生成特征描述子

首先初步定位特征点，将经过矩阵处理后的点与三维临域内的26个点的灰度值进行比较，寻找最值点作为关键点。然后用适当的阈值，从关键点中筛选出精确的特征点,如图1a)所示。

初步定位特征点后，将Haar小波响应值根据距离中心点远近加权，然后将在角度60°、半径6δ(特征点尺度值)的扇形范围内的x,y方向的Haar小波响应求和并形成矢量，其中Haar小波边长为4δ。旋转36°，重复上述步骤直至遍历整个圆形区域，即可得到特征点的主方向，如图1b)所示。

如图2所示，以特征点为中心，特征点的主方向为方向，边长为20δ，构成正方形框。然后分为16个子区域，每个子区域中又有25个像素点，统计就主方向而言的x,y方向的Haar小波响应值。那么，每个子区域就有4个值，分别为25个像素点的水平方向总和，水平方向绝对值总和，垂直方向总和，垂直方向绝对值总和，因此SURF的特征描述子具有16×4=64维向量。

1.2 基于SURF算法的二帧差分法

本文设计基于SURF特征匹配的方法，进行二帧差分。首先提取SURF特征点，然后利用FLANN(fast library for approximate nearest neighbors)算法进行初步匹配，之后利用RANSAC(random sample consensus)[14]算法得到投影映射矩阵。根据得到的矩阵进行背景运动补偿并进行差分，最后得到在移动摄像下物体的真实运动，具体流程如图3所示。

2 移动摄像下的目标跟踪算法

由于卡尔曼滤波和Mean Shift算法比较经典，读者可自行查阅相关文献，本文主要介绍移动摄像下的目标跟踪算法设计。

传统的Mean Shift算法在目标出现机动过快、受到遮挡、旋转缩放时，很难精准跟踪目标。本文首先整合了基于SURF特征点匹配算法的二帧差分法以解决移动摄像下的相对运动和旋转缩放等问题，然后引入卡尔曼滤波，借助滤波器的预测能力，解决目标机动过快的问题，最后利用Bhattacharyya相似性系数更新卡尔曼滤波的误差协方差矩阵有效地解决目标遮挡问题。算法流程图见图4，具体步骤如下：

(1) 读取视频，提取相邻帧的SURF匹配特征点，并利用第2节的方法进行二帧差分，得到前景运动目标。

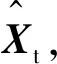
(3) 利用Bhattacharyya相似性系数进行相似性度量，并利用偏移向量不断迭代最终得到目标准确位置。

(4) 利用Bhattacharyya相似性系数更新卡尔曼滤波的误差协方差Pt。

(5) 重复以上步骤，直到视频结束。

3 实验结果分析

本文算法可实现手动框选目标的交互跟踪和预先输入目标面积的自动跟踪，实验平台为2.8 GHz Intel Core i7-770HQ处理器、16 GB内存、64位操作系统计算机，仿真环境为Python语言，在VIVID视频集[15]中的4个视频序列进行性能测试，算法每帧的处理速度在100 ms左右，基本达到实时性要求，下面列出了本文算法、组合卡尔曼滤波和Mean Shift算法、Mean Shift算法、高斯滤波跟踪算法的跟踪结果。

3.1 算法定性分析

图5 EgTest01序列中，由于成像传感器的快速移动，目标在13帧(图5第1行图像)左右产生运动模糊，导致其余3种跟踪算法均有一定程度误差偏移；当传感器出现抖动时(第34帧，图5第2行图像)，由于采用本文设计的二帧差分法，可以继续跟踪目标，其他算法均跟踪失败。

图6 EgTest04序列中，成像传感器掉帧，时而无运动，时而跳跃向前。跟踪开始后(第3帧，图6第1行图像)，由于掉帧，目标无运动。由于采用本文设计的特征匹配，依然可以很好地跟踪目标，其他算法均不同程度向前偏移。在第22帧(图6第2行图像)时，目标掉帧，跳跃向前，只有本文算法未受干扰继续跟踪。

图7 EgTest05序列中，当跟踪目标被树木遮挡时(第244帧，图7第1行图像)，Mean Shift算法由于遮挡干扰，偏离目标严重；组合了卡尔曼滤波的Mean Shift算法由于具备了预测功能，遮挡时依然能够跟踪目标，但只能跟踪单个目标；本文算法未受干扰。后续跟踪中，目标受到完全遮挡后再次出现(第264帧，图7第2行图像)，这种跟踪目标的突然消失导致了其他3种算法的失败，本文算法由于采用SURF算法的特征匹配，依然具有良好的跟踪效果。

图8 RedTeam序列中，由于摄像机缩放，目标由小变大，再变小，出现了较大的尺度变换，由于高斯滤波在此例中效果无法跟踪目标，不予列出；Mean Shift和卡尔曼滤波、Mean Shift没有自适应能力，虽然可以进行跟踪，但在目标发生尺度变换时跟踪窗口保持不变，性能较差，本文算法保持了良好的自适应能力。

综上所述，本文算法组合了基于SURF的二帧差分法、卡尔曼滤波和Mean Shift算法，各部分优势互补，充分解决了移动视频下跟踪过程中目标的大尺度变化、遮挡和快速移动等问题，极大提升了跟踪性能。

3.2 算法定量评价

图9给出了本文算法和其他3种比较算法在VIVID视频集中的像素误差曲线。像素误差是物体真实位置中心与跟踪算法预测中心的欧氏距离，像素误差的数值可以直接表现出算法对跟踪目标的鲁棒性。本文通过逐帧计算目标像素误差的方式评估算法的跟踪性能。

很明显，在对移动视频序列目标的跟踪中，传统的高斯滤波跟踪无效；Mean Shift跟踪算法在一般情况下跟踪效果较差，尤其在目标出现遮挡、尺度变化等情况时，跟踪性能急剧下降，很难保证跟踪的鲁棒性和稳定性；组合卡尔曼滤波后，组合算法在遇到上述特殊情况时跟踪效果有了一定改善，但跟踪性能依旧无法实现大幅度提升；本文算法在组合算法的基础上，融合了基于SURF的二帧差分法后，保证了整体视频序列的跟踪效果。

综上所述，本文设计的二帧差分法可以有效解决成像传感器大尺度缩放、高速相对移动等负面影响。同时，差分过程中的特征提取也很好地解决了目标突然运动、受部分或全部遮挡等跟踪问题，相较于其他3种算法，具有更好的跟踪性能。

4 结束语

针对移动摄像下的目标跟踪问题，本文提出了一种新的跟踪算法。首先利用基于SURF算法的二帧差分法提取前景运动目标，然后利用卡尔曼滤波和Mean Shift算法进行后续目标跟踪。本文算法充分利用了二帧差分法对移动摄像的适用性，SURF算法的尺度和旋转不变性，卡尔曼滤波的估计最优性以及Mean Shift跟踪算法的迭代稳定性。本文的实验完全模拟了空中武器设备跟踪地面运动目标时可能出现的问题。实验结果及分析表明，在反坦克等军事领域中，本文算法可以很好地解决成像传感器的掉帧、突然抖动和高速移动问题，也可以极大提高对受遮挡或大尺度变化目标的跟踪能力。