带有死区环节的电动舵机鲁棒控制技术*

李宗星，张锐

(北京电子工程总体研究所，北京 100854)

0 引言

电动舵机因其具有结构简单、工艺性好、可靠性高、使用维护方便、成本低廉的特点，在导弹武器系统中应用逐渐增多。特别是近些年来，电动舵机的性能又有了很大的提高，所以受到了工程技术人员更加广泛的关注。

死区特性是电动舵机中常见的一种非线性环节。通常，将系统当中输入值无法进行响应的区域定义为死区[1-3]。电动舵机中死区的存在会影响舵机的响应特性和控制精度。在死区特性并不明显或者死区范围很小时，将死区环节近似处理成线性环节，在某些工程应用上是可行的[4-7]。但是，随着导弹武器系统对于控制精度要求的逐渐提高，对电动舵机的响应特性和控制精度的要求也逐渐提高，这种近似处理的方法会缩小系统正常工作的范围，并且使系统性能显著下降，严重时甚至会造成系统的控制失败[1]。

鲁棒控制是在滑模控制方法的基础上改进发展来的，它通过加大控制输入，对系统中的扰动及不确定动态进行有效抑制，并且避免了滑模控制产生的抖振的不利影响[8-15]。近年来，在工程领域中，鲁棒控制方法有着广泛的应用，文献[8]中提出了一种作用于机床的鲁棒控制方法，对系统中的扰动及不确定动态有较好的抑制作用。本文中将电动舵机的死区环节处理为线性环节与扰动的结合，设计鲁棒控制器，最后通过仿真与PD控制比较，验证该控制方法的有效性。

1 系统模型及分析

1.1 电动舵机模型

将电动舵机的模型整理并适当简化，简化后的电动舵机系统示意图如图1所示，其为一个单输入单输出系统。

图1中，y为舵面偏转角，yd为输入指令，u为PD控制器输出，w(u)为死区环节输出。图中虚框部分为线性环节，包括：控制器输出电流到电机控制电压的转换模块、电机环节(输入为电机控制电压，输出为电机旋转角速度)、电机旋转角速度与舵面偏转角的转换模块。其中，Ua为控制器输出电流到电机控制电压的传递系数，Km为电枢电流到电机力矩的传递系数，Ke为电机旋转角速度到电枢反电势的传递系数，N为电机旋转角速度(弧度制)到舵面偏转角速度(角度制)的传递系数，La为电枢绕组的电感(H)，Ra为电枢绕组的电阻(Ω)，J为活动部分折算到舵面转轴上的惯性矩(m4)。

死区模型如图2所示。

其数学表达模型如下：

(1)

图1中虚框所示线性部分可进一步整理成式(2)中传递函数，其中各符号参数取值如表1所示。

(2)

1.2 电动舵机PD控制器分析

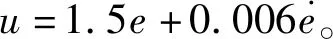
当死区区间为[0,0]时，即无死区时，对图1所示的电动舵机性能进行分析。此时，系统的奈奎斯特曲线和阶跃响应曲线分别如图3，4所示。

由图3可知，奈奎斯特曲线不包围(-1,j0)，且开环传递函数的正实部极点个数为0。由奈式稳定判据可知，闭环系统稳定。由图4可知，系统超调量σ%=5%，调节时间ts=0.039 2 s，上升时间tr=0.007 2 s。可见当不考虑死区特性时，在当前控制参数下电动舵机系统工作性能良好。

下面分析不同死区特性对该电动舵机跟踪指令的影响。由于仿真结果不仅与死区特性本身有关，也受输入指令的影响，所以为便于分析，本文仅比较输入指令为阶跃指令和幅值为1频率为10 Hz的正弦指令时的结果。

令系统初始状态均为0。输入指令为yd=sin(20πt)。死区分别取为[0,0]，[-0.05,0.05]，[-0.5,0.5]时，仿真结果如图5～7所示。

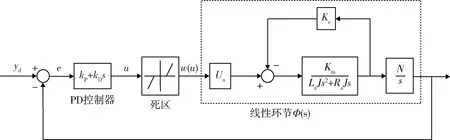
图1 电动舵机模型Fig.1 Electromechanical actuator model

图2 死区模型Fig.2 Dead zone model

表1 系统参数Table 1 System parameters

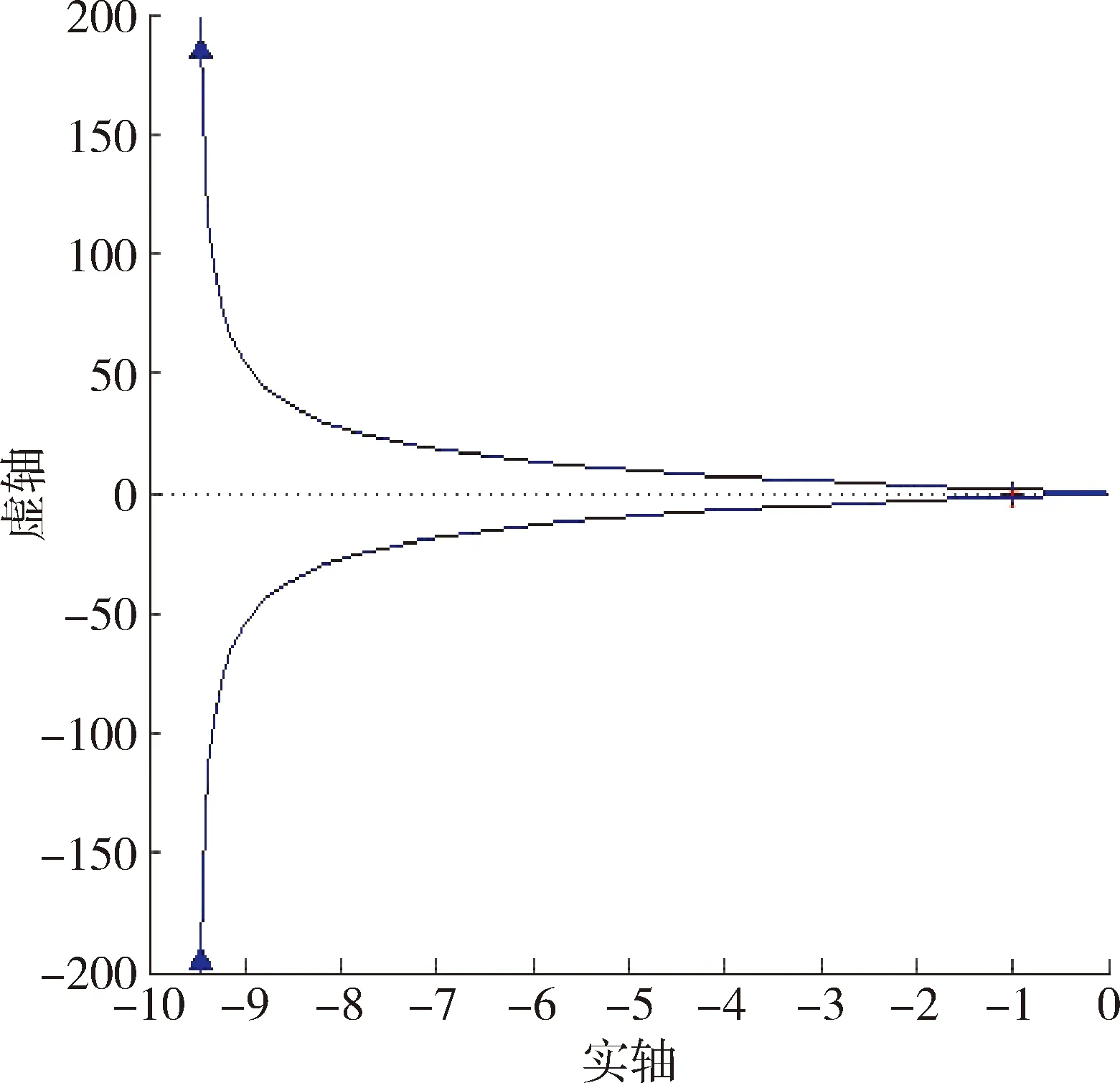
图3 奈奎斯特图Fig.3 Nyquist diagram

显然，死区环节的存在会对PD控制器的控制效果产生影响。在图5中，无死区时，最大跟踪误差为0.081 6°，系统输出可以有效跟踪输入指令。在图6中，死区区间为[-0.05,0.05]时，最大跟踪误差为0.115 4°，系统输出与输入指令之间也是基本重合。在图7中，死区区间为[-0.5,0.5]时，系统输出与输入指令之间出现较大偏差，最大跟踪误差达到0.431 2°，峰值处时间延迟为0.012 9 s，此时认为在给定正弦指令yd=sin(20πt)下系统输出不能有效跟踪输入指令。

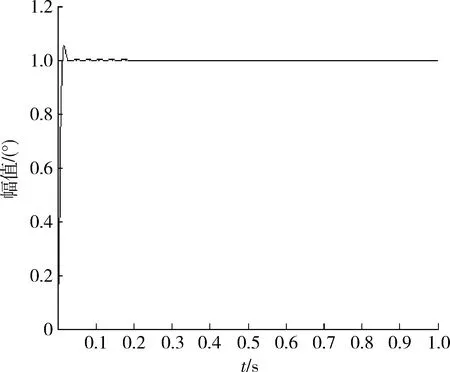
图4 阶跃响应曲线Fig.4 Step response

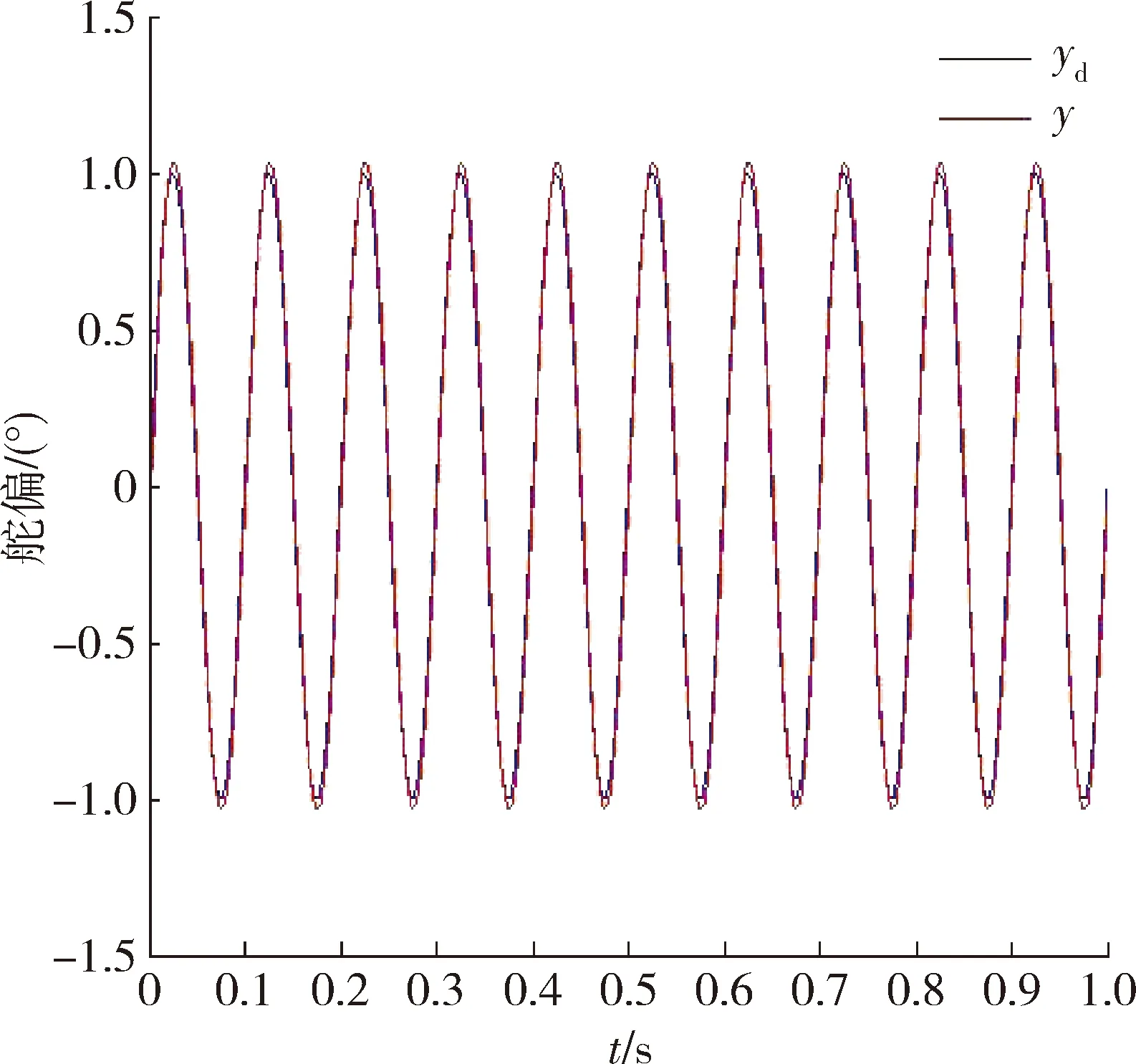
图5 PD控制结果(无死区时)Fig.5 Result of PD controller (without dead zone)

图6 PD控制结果(死区为[-0.05,0.05])Fig.6 Result of PD controller (with dead zone[-0.05,0.05])

图7 PD控制结果(死区为[-0.5,0.5])Fig.7 Result of PD controller (with dead zone [-0.5,0.5])

进一步量化比较不同死区特性对系统的影响，结果见表2。

由表2可见，死区特性对超调量和跟踪误差有较大影响。死区范围较小时，系统超调量呈增大趋势(由无死区时的5.01%增大到死区为[-0.05,0.05]时的9.94%)。当死区范围增大到一定程度时，系统超调量会减小，并逐渐接近于0(死区为[-0.5,0.5]时，超调量已下降到0.67%)。可以将死区环节理解成一种特殊的变增益环节，死区区间越大，增益越小。再将系统近似简化为二阶系统分析(下文设计鲁棒控制器时会详细介绍)，计算其阻尼比，可得变化趋势为先减后增，则超调量为先增后减。随着死区范围的增大，跟踪误差也会不断增大(阶跃响应稳态误差绝对值由无死区时的0增大到死区为[-0.5,0.5]时的0.328 6°，正弦指令下跟踪误差上限由无死区时的0.081 6°增大到死区为[-0.5,0.5]时的0.431 2°)。

因此，在死区范围较小时，可以将其近似处理为线性环节，并进行控制器的设计。此时，系统跟踪误差较小，可忽略死区带来的影响。但是，当死区范围较大时，采用近似方法处理的结果会使闭环系统的输出与输入指令之间产生较大的偏差，严重影响了控制效果。本文中认为在阶跃指令和正弦指令yd=sin(20πt)下，死区区间超过[-0.2,0.2]时不能近似处理，此时阶跃响应稳态误差0.097 1°，正弦指令跟踪误差绝对值范围为[0,0.223 8]。针对这种情况，在对电动舵机进行设计时需要考虑死区环节的作用。

2 电动舵机鲁棒控制器设计

以上的仿真分析表明，当存在死区时，为确保电动舵机的控制精度和响应特性，在设计电动舵机时需要将死区特性的影响考虑进来。下面介绍的一种鲁棒控制方法中，将死区的作用分解为了线性增益与扰动的合成，再设计控制器对扰动进行抑制。本文将这种方法引入到电动舵机控制系统设计中。

2.1 滑动变换及其性质

考虑如下n阶系统：

(3)

在状态空间中定义如下变换：

(4)

定义滑动平面如下：

Q={p|p=0 }.

表2 PD控制结果Table 2 Result of PD controller

定理1对于式(4)所定义的滑动变换，信号p(t)与e(t)之间具有以下性质[1]：

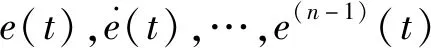
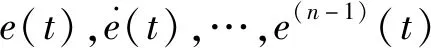
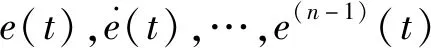
2.2 模型简化处理

考虑到图1所示电动舵机系统中La，J均为小量，故可先将三阶传递函数简化为二阶传递函数，再设计电动舵机控制器(仿真验证时仍基于三阶模型进行)。简化后线性部分传递函数如下：

(5)

死区环节可处理为线性环节与扰动的合成，处理后死区环节模型为

w(u)=u+σ,

(6)

注意该扰动上下界为已知，即|σ|≤Δ。

2.3 鲁棒控制器设计

将图1所示电动舵机系统模型写成如下形式：

(7)

设计鲁棒控制器如下：

(8)

式中：k为正常数；kr(p)为p的函数。

将式(8)代入(7)得

-kp-kr(p)p-σ.

(9)

定理2当鲁棒控制项u2的第2项满足如下条件时，系统能够在有限时间内达到边界层。

(10)

式中:ε为正的设计参数。

证定义李雅普诺夫函数如下

(11)

对式(11)求导，并将式(9)和式(10)代入得

(12)

求解式(12)得

(13)

将式(11)代入式(13)得

(14)

显然，系统能够在有限时间内达到边界层。

定理3下面给出一种满足式(10)的kr(p)的取值

(15)

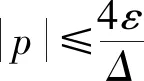
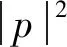
(16)

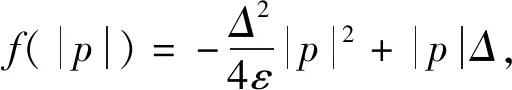
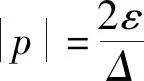
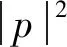
(17)

即p{-kr(p)p-σ}≤0<ε成立。

2.4 仿真结果及分析

鲁棒控制器参数设计为a1=100，k=0.02，ε=0.05。系统初始状态均为0。死区范围为[-0.5,0.5]。输入指令为yd=sin(20πt)。注意仿真时使用模型为未简化模型，即线性环节传递函数为式(2)。仿真结果如图8,9所示。

进一步量化比较鲁棒控制结果与PD控制结果见表3。

图8 鲁棒控制结果Fig.8 Result of robust controller

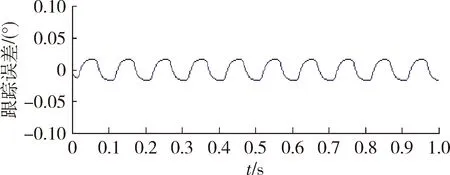
图9 鲁棒控制跟踪误差Fig.9 Tracking error of robust controller

由表3可见，死区区间为[-0.5,0.5]时，鲁棒控制器超调量为0，阶跃指令下稳态误差仅为PD控制器的4.4%，正弦指令下跟踪误差绝对值上限减小至PD控制器的3.8%，峰值处时间延迟减小至PD控制器的1.55%。显然，鲁棒控制器优势明显。

通过本文的研究可以得出以下几点结论：

(1) 在存在较大范围死区时(死区区间超过[-0.2,0.2])，本文将死区环节分解为线性环节和扰动，并设计由式(8)和式(15)构成的鲁棒控制器。该控制方法与PD控制方法相比，控制效果有明显提高(超调量为0，跟踪误差明显减小)，能够实现对输入指令的有效跟踪。

(2) 在进行控制器的设计时，电动舵机模型的简化处理是可行的。考虑工程实际中，电动舵机的工作频率范围可以解释简化处理可行的原因。

表3 PD控制结果与鲁棒控制结果Table 3 Results of PD controller and robust controller

3 结束语

本文针对死区特性造成的系统输出偏离输入指令的问题，采用将死区环节分解并设计鲁棒控制器的方法，提高了系统的控制精度，实现了对输入指令的有效跟踪。但是，通过前面的数据对比，也发现了鲁棒控制方法对于系统的改善主要在于跟踪误差的减小，而如何提高响应的快速性还需要进一步分析研究。

鲁棒控制方法的应用不仅仅限于对死区环节的处理，同样可以扩展到摩擦、齿隙等非线性环节的处理上。在本文中对死区环节的处理是将其分解为线性环节与扰动的结合，这种思路对摩擦、齿隙等非线性环节的处理同样可行。

在实际工程应用中，舵机系统也存在外界扰动和参数摄动。在对外界扰动和参数摄动的模型具有一定了解的前提下，也可将其与系统中非线性环节处理得到的扰动部分一起处理，并用鲁棒控制方法进行抑制。