快堆燃料组件少孔式管脚替代方案水力实验研究

秦亥琦，陆道纲，司 宇，刘少华，唐甲璇，钟达文

(1.华北电力大学 核科学与工程学院，北京 102206；2.华北电力大学 非能动核能安全技术北京市重点实验室，北京 102206)

钠冷快堆作为我国核能发展基本战略的第2步，具有提高铀资源利用率、嬗变高放长寿命核废料以减轻环境压力等突出优势，因而成为了我国核能发展的重要技术选择[1]。有关快堆结构设计、热工流体力学等成为了国内外研究的热点。管脚作为快堆燃料组件的入口，其结构尺寸对燃料组件的冷却剂流量分配、压力损失等流体力学行为有着重要影响，直接关系到快堆的安全性与经济性，因此有必要针对快堆燃料组件管脚的流动特性进行深入研究。

丁振鑫[2]提出了中国实验快堆(CEFR)燃料组件阻力系数的计算方法，结果显示该方法计算精度较高，满足工程需要；冯预恒等[3]使用计算流体动力学(CFD)软件CFX对CEFR Ⅰ-Ⅱ型栅板联箱截流件流动阻力特性进行了数值模拟，结果显示数值模拟的结果可靠；冯预恒等[4]利用CFX软件对CEFR Ⅰ型小栅板联箱及其节流件进行了数值模拟，研究了联箱内7个燃料元件管脚入口的流量分配；李淞等[5]采用Fluent软件对169根棒的快堆燃料组件棒束进行了数值模拟，其计算结果与实验结果吻合良好；李淞等[6]利用Fluent软件研究了快堆组件稠密棒束中的冷却剂流动方式，计算结果显示横向流与轴向流在不同位置与方向上呈现出不同的流动特性；Jeong等[7]利用CFX研究了日本回路式钠冷快堆Monju的37根带绕丝燃料棒束内部的三维流动现象，结果显示内部子通道中存在小范围的漩涡，且边缘与边角子通道中的二次横向流动强于内部子通道；Hamman等[8]研究了19根带绕丝燃料棒束内部的流动特性，结果显示数值模拟中湍流模型对计算结果有较大影响，同时棒的光滑程度以及绕丝结构均会对流动特性产生一定影响；Gajapathy等[9]以印度的原型快堆作为研究对象，利用数值模拟方法研究了7根带绕丝燃料棒束的流动特性。上述研究多集中于快堆燃料组件棒束段及其节流件的热工流体力学特性，而管脚段相关研究较为缺乏，尤其是管脚的结构设计标准尚待于进一步明确。

本文针对工程中广泛应用的多孔式管脚存在的缺陷，提出少孔式管脚替代方案，用以简化管脚结构达到降低加工废品率、精确调节管脚流动特性的目的，并通过水力实验验证该替代方案的可行性。

1 快堆燃料组件少孔式管脚替代方案

管脚位于快堆燃料组件入口处，冷却剂钠经由小栅板联箱分配后通过管脚开孔进入燃料组件内部，自下而上流经燃料棒束，流动过程中带走燃料释热，实现对燃料棒的有效冷却，最终由顶部操作头流出至热钠池[10]。管脚开孔孔径十分有限，冷却剂通过时由于流动面积骤减导致流束收缩、流速加快、能量耗散加剧，故管脚段压降成为燃料组件总压降的主要部分。图1示出快堆燃料组件示意图。

图1 快堆燃料组件结构示意图

Fig.1 Structure schematic of fast reactor fuel assembly

文献[11]显示，在快堆堆芯中燃料组件呈分区布置形式，不同区域的燃料组件对应的功率不同，因而所需的冷却剂流量也存在较大差异。通过改变管脚开孔孔径调节进入不同区域燃料组件的冷却剂流量，使得不同区域的燃料组件具有大致相同的压降以维持堆芯压力平衡。目前工程中广泛采用多孔式管脚，其共设置有24个开孔，布置在管脚中部位置，按照4排6列的形式等间距分布。加工过程中利用钻头进行打孔，由于管脚开孔数量较多，使得产品废品率较高且不利于提高加工效率。此外，由于钻头自身存在一定锥度，故无法保证内、外孔径严格一致，加工精度较差，在开孔数量较多的情况下，上述加工误差不断累积，不利于精确调节管脚流动特性。基于上述对传统多孔式管脚的缺陷分析，本文提出了少孔式管脚替代方案，将开孔数量从24个削减至6个，通过合理扩大孔径使得两类管脚具有近于相同的流动特性，既有利于控制加工误差、提高加工效率，还有利于管脚流动特性的精确调节。此外，少孔式管脚开孔数量大幅减少且不改变管脚壁厚，因此结构强度保守。图2示出多孔式、少孔式管脚结构示意图，图2中箭头为管脚内部冷却剂流动方向。

a、b——多孔式管脚；c、d——少孔式管脚图2 快堆燃料组件管脚结构示意图

少孔式管脚开孔与多孔式管脚最下方一排开孔处于同一高度位置，除开孔数量外其他结构完全一致，按照1排6列的形式等间距分布。

2 水力实验研究

2.1 实验原理与基本参数

本实验属于非破坏性验证实验，目的在于研究多孔式与少孔式两类管脚的流动特性，验证少孔式管脚替代方案的可行性。设计要求管脚在钠工质流量为13 kg/s时，对应的压降达到240 kPa，压降相对误差控制在3%以内。本实验选择去离子水作为实验工质，需针对钠-水进行基本参数的相似性转换。根据流体力学相似性原理，由起主导作用的定性准则确定实验温度，本实验属于有压不可压缩黏性流体的管内流动，因此流体黏滞力起主导作用，故使用雷诺相似准则进行相似性计算[12]。雷诺数Re是表示黏性流体流动过程中所受惯性力与黏性力之比的无量纲数[13]：

Re=ρvd/η

(1)

式中：ρ为密度；v为流速；d为水力直径，本文取为管脚内径；η为动力黏度。

雷诺相似准则为：

ReNa=ReH2O

(2)

工程中管脚段冷却剂钠对应温度为360 ℃，在该温度下计算各项物性参数，结果列于表1[14]。各项物性参数的计算关系式如下。

表1 钠的物性参数

液态金属钠密度ρ为：

ρ=972.5-20.11×10-2t-1.5×10-4t2

(3)

式中，t为摄氏温度。

动力黏度η为：

η=0.123 5×10-4ρ1/3e0.697ρ/T

(4)

式中，T为开氏温度。

实验对象为快堆燃料组件全尺寸、全配重模拟件，单值条件相同，因此由式(2)可得360 ℃钠工质对应水工质温度为84 ℃，在该温度对应关系下，两类工质具有相同的流动特性。压力分布由欧拉相似准则确定，其中欧拉数Eu是表示总压力与惯性力比值的无量纲数[13]：

Eu=Δp/ρv2

(5)

式中，Δp为压降。

欧拉相似准则为：

EuNa=EuH2O

(6)

根据流体力学相关理论，实验中需测定各相似准则中所包含的应予测定的一切物理量[12]。由于快堆燃料组件原型与模拟件的结构尺寸及实验工质物性均为单一条件，故本实验中仅需测量通过燃料组件模拟件的流量与对应压降即可。表2列出实验基本参数。

表2 实验基本参数

2.2 实验台架简介

依托华北电力大学非能动核能安全技术北京市重点实验室所属大型快堆水力实验台架开展相关实验。实验台架工艺流程如图3所示。

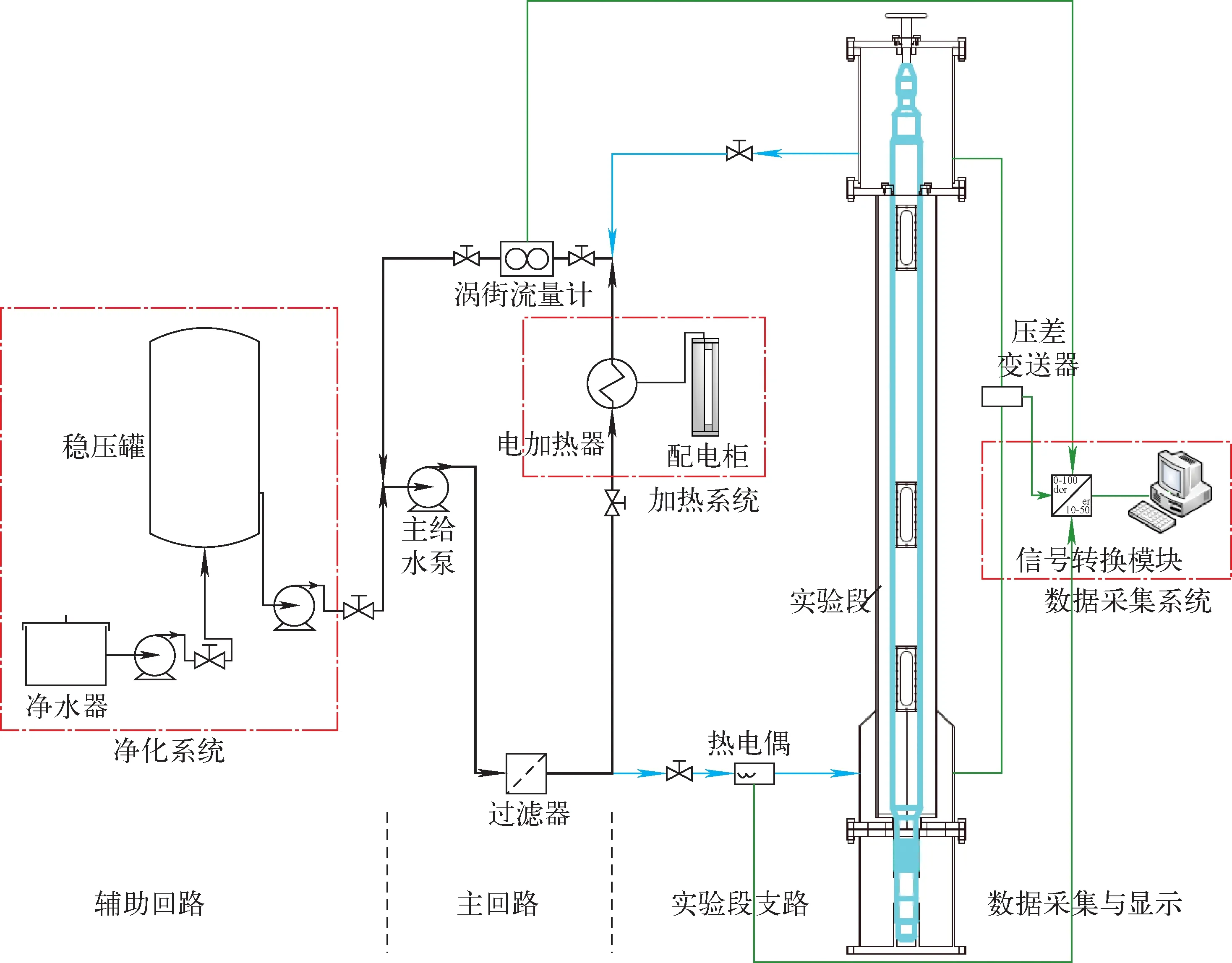
黑色粗连接线为主回路流程，蓝色细连接线为经实验段支路流程，绿色连接线为数据采集线路流程图3 实验台架示意图

实验台架共分为5个子系统，分别为净化系统、主回路、实验段、加热系统与数据采集系统。净化系统由净水器、循环泵、高位给水箱、过滤器及配套阀门组成，由于燃料组件模拟件结构十分精细，若实验工质中存在杂质，极易引起表面结垢甚至出现杂质堆积堵塞流动通道，因此实验利用净水器制备去离子水(电导率小于0.5 μs/cm)，净化后的去离子水在高位给水箱中暂存，实验前经循环泵打入并充满实验回路。主回路包括管道、主给水泵以及对应阀门，当实验回路中充满水时，通过主给水泵实现工质循环，在主回路与实验段支路中稳定流动。加热系统包括1台电加热器，在实验工质流动过程中，启动加热器将实验工质加热至预定实验温度(84 ℃)。数据采集系统包括流量计、差压变送器以及控制台，实现燃料组件模拟件流量与压降的自动采集，并实时监测实验系统温度，上述参数经过信号转换模块在PC端完成显示、实时监控与存储。

实验段为不锈钢材质，总高为5 m，整体为三段式结构，自下而上依次为下封头、中部套筒、上封头，三者之间通过法兰相互连接。下封头通过地脚螺栓固定在地面上。中部套筒在竖直方向上设置有观察窗，便于观察内部流动情况。上、下封头等径。实验段内部放置被测量的燃料组件模拟件，模拟件轴线与实验段轴线保持共线，由上封头顶部安装的丝扣保持模拟件的压紧与对中。实验工质由下部实验段入口进入，流经燃料组件模拟件后由顶部出口流出，通过调节主给水泵频率与电动调节阀开度实现对流量、压降的精确控制与工况的切换。

2.3 数据处理与不确定度

以额定压降为基准，每隔5%设置1组工况，实验过程中每组工况保持3～4 min，去除工况调节前后变化幅度较大的数据，确保每组工况得到100组左右有效数据；对上述数据取平均值后作为该组工况流量与对应的压降；基于相似性分析，将水工质实验数据转换为对应的钠工质数据；由于测量仪器波动、调节手段灵敏度等原因，额定工况实验数据无法通过原始数据直接获得，为尽可能模拟钠工质流动特性，本文将各实测工况点数据进行拟合获得流动特性曲线，再利用该曲线表达式计算额定流量对应的压降，当实测压降与额定压降间的相对误差在3%以内时，认为该管脚结构尺寸满足设计需求。

本实验不确定度来源主要包括数据处理方法与仪器误差，经评估，管脚压降总相对不确定度为0.31%，流量相对不确定度为0.99%。

3 结果分析

3.1 实验结果

本文分别针对不同孔径的多孔式与少孔式两类管脚进行了水力实验，钠工质的实验结果列于表3。

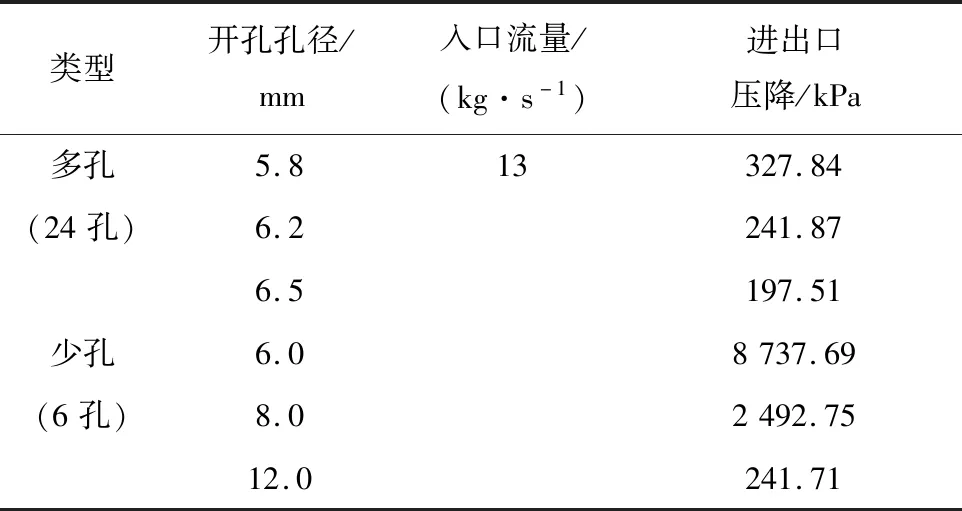
表3 快堆燃料组件管脚实验结果

由表3可见，两类管脚随管脚孔径的减小，节流能力依次增强，对应的进出口压降增大。少孔式管脚节流能力远强于多孔式管脚，相应其管脚孔径的调节效率更高。图4示出两类管脚的流动特性曲线。

孔径为6.2 mm的多孔式管脚与孔径为12.0 mm的少孔式管脚在入口流量为13 kg/s时，实测压降与额定压降相对误差均在3%以内，满足设计需求。由图4可知，孔径为6.2 mm的多孔式管脚与孔径为12.0 mm的少孔式管脚对应的流动特性曲线几乎重合，二者具有近乎相同的流动特性，可达到替代效果。由此证明本文所提出的少孔式管脚替代方案可行，可在简化管脚结构的基础上通过合理扩大孔径保持与多孔式管脚相同的流动特性。

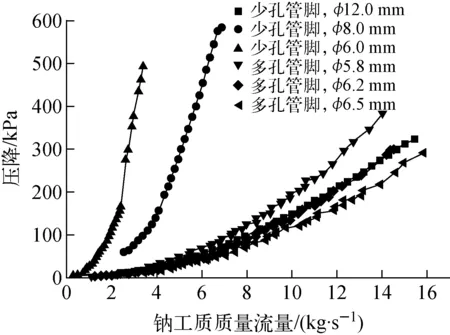
图4 快堆燃料组件管脚的流动特性曲线

3.2 阻力特性

冷却剂在快堆燃料组件管脚内部的流动过程十分复杂，流通面积、流动方向等频繁变化，对分析管脚的流动特性带来较大困难。本文采用等效替代的思想将整个管脚视为1个阻力件，研究其阻力特性的变化。根据达西-魏斯巴赫公式，管内流动压降与阻力系数满足如下关系[12]：

Δp=0.5fρv2

(7)

式中，f为阻力系数。f是以Re为自变量的函数，反映了流动的阻力特性，通常情况下由实验确定。由于两类管脚阻力系数变化范围差异较大，图5示出两类管脚的阻力特性曲线。

由图5可见，各类管脚在Re超过某一限值时，阻力系数基本趋于稳定，由此认为流动状态进入自模区[12]，各类管脚自模区对应的平均阻力系数列于表4，用于一般估算。由图5a、b、d可知，少孔式管脚节流能力较强，其阻力远超多孔式管脚。由图5c可知，孔径为6.2 mm的多孔式管脚与孔径为12.0 mm的少孔式管脚阻力特性曲线基本吻合，证明本文所提出的少孔式管脚替代方案可行。其中少孔式管脚(12.0 mm)的阻力系数略高于多孔式管脚(6.2 mm)，这主要是由于本文计算Re时采用均一化处理，均以管脚内径作为水力直径，实际两类管脚在开孔处流速不同，造成阻力系数存在轻微差异。此外，棒束结构相同时，在相同压降下少孔式管脚局部阻力占燃料组件沿程阻力的份额大于多孔式管脚。

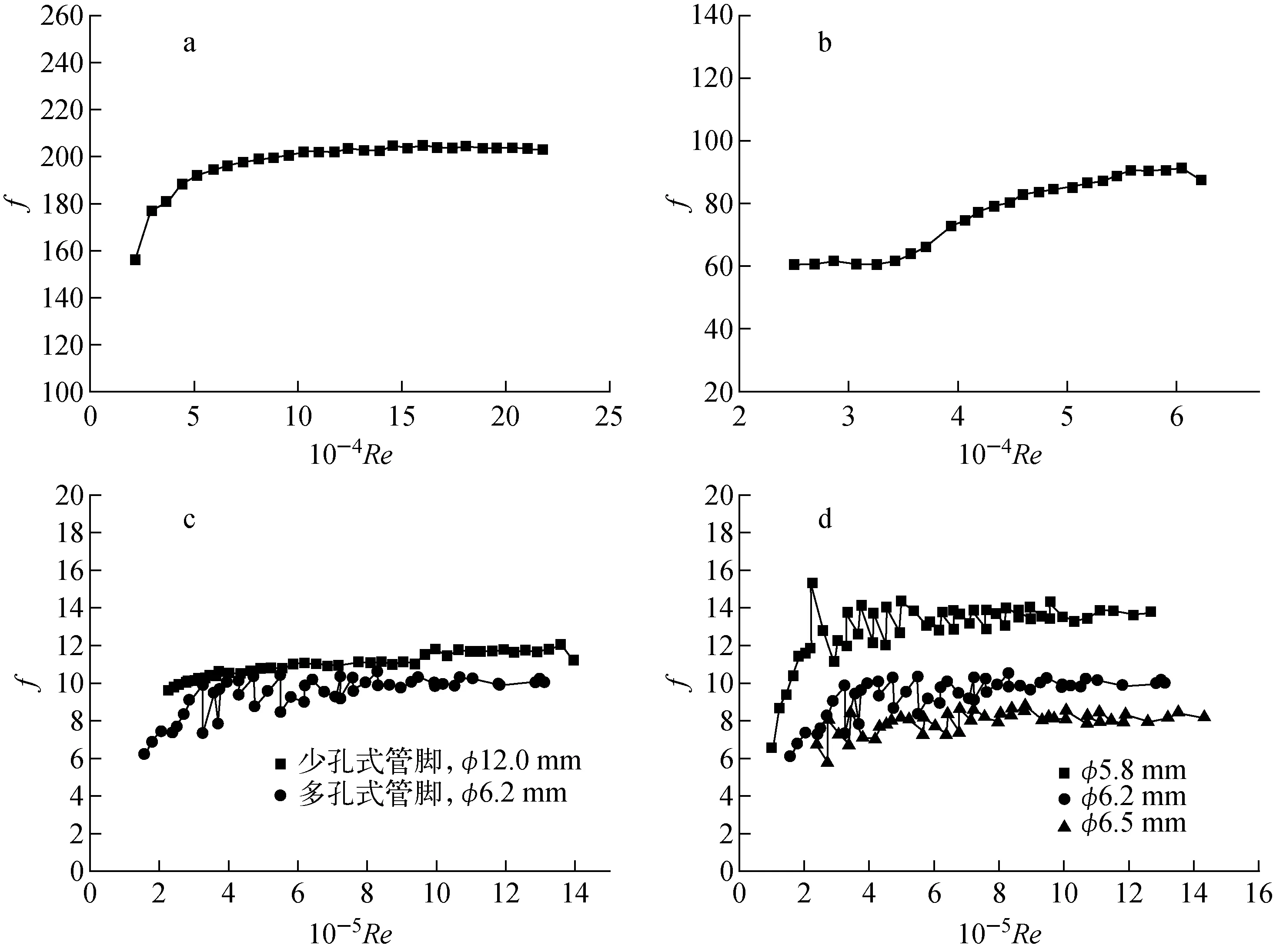
a——少孔式管脚，φ6.0 mm；b——少孔式管脚，φ8.0 mm；c——替代管脚；d——多孔式管脚图5 快堆燃料组件管脚的阻力特性

表4 快堆燃料组件管脚的阻力系数

根据连续性方程：

vaAa=vbAb

(8)

式中：va、vb分别为截面a与b处对应的流速；Aa、Ab分别为截面a与b的流通面积，本文中截面a、b分别取燃料组件管脚开孔所在平面与管脚出口平面。由此可将开孔处流速折算为管脚出口处流速，该流速可由Re计算而得。故式(7)转化为：

Δp=0.5fμ2Re2/d2

(9)

式中，μ为流体运动黏度。

10-3S2-2.126S+479.5

(10)

式中，S为管脚处总流通面积。

S=nπR2

(11)

式中：n为管脚开孔数；R为管脚开孔半径。

式(10)定性温度为管脚段钠工质温度，本文取为360 ℃；定性尺寸取开孔孔径，其直接决定管脚开孔处流通面积；出于保守考虑，上述经验公式对应管脚开孔孔径适用范围为5.8～12.0 mm。

3.3 流场分布

作为水力实验的补充，本文采用CFD方法针对两类管脚流动特性进行了初步数值模拟，定性研究其内部流场分布。在CFX软件中选择适用于高雷诺数流动的k-ε湍流模型配合scalable壁面函数[15]。在保证网格质量的前提下，采用网格一体化设置，自动生成四面体非结构网格。为尽可能提高网格质量，使得流动过渡稳定，内、外壁面处各设置5层边界层。快堆燃料组件管脚均采用不锈钢材质进行精加工，由壁面粗糙度所引起的附加切应力极小，故不考虑内、外壁面粗糙度的影响。最终采用单元数为728万的网格系统。

图6示出数值模拟结果与实验结果对比。由图6可知：钠工质质量流量在6～15 kg/s(5.48×105≤Re≤1.35×106)范围内时，数值模拟结果与实验结果吻合良好，二者间的相对误差不超过5%；在13 kg/s额定工况时，数值模拟结果与实验结果相对误差不超过1%；在低流量靠近层流区范围内，数值模拟结果误差较大。说明在本文设计需求对应流量范围内，数值模拟结果可靠。

图7示出两类管脚开孔附近的速度分布。由图7可见：两类管脚速度场均呈对称状分布，在管脚开孔附近形成高速区，在管脚轴线与开孔轴向相交处由于流体相互碰撞，形成低速核心，该低速核心沿流动方向逐步消失；多孔式管脚由于不同高度开孔相互干扰，导致在近壁面处形成了较大面积的低速区，不利于管脚壁面的对流换热；少孔式管脚流动发展相较于多孔式管脚更为旺盛。

图6 数值模拟结果与实验结果对比

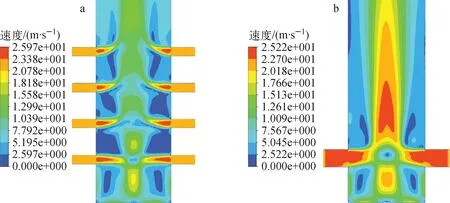
a——多孔式管脚，φ6.2 mm；b——少孔式管脚，φ12.0 mm图7 快堆燃料组件管脚局部速度分布

4 结论与展望

本文基于对传统快堆燃料组件多孔式管脚的缺陷分析，提出了少孔式管脚替代方案，既有利于控制加工误差、提高加工效率，还有利于管脚流动特性的精确调节。通过水力实验验证了该替代方案的可行性，结果显示孔径为12.0 mm的少孔式管脚与孔径为6.2 mm的多孔式管脚具有几乎相同的流动特性，均满足设计需求，可达到替代效果，本文所提出的少孔式管脚替代方案可行。通过水力实验研究了多孔式与少孔式两类管脚的阻力系数分布、流量与压降对应关系等流动特性，为快堆燃料组件管脚的结构设计提供了必要参考。

本文给出了适用于多孔式与少孔式两类管脚的阻力系数与结构尺寸间的经验关系式，可用于一般估算，供相关实验或工程参考。本文中所开展水力实验的管脚数量有限，因此拟合得到的阻力系数经验关系式可能存在一定偏差，后续需要扩充实验内容加以完善，提高计算精度。