基于GLCM和Gabor纹理特征的手势识别算法

李云峰 张澎悦

(河南科技大学机电工程学院 河南 洛阳 471003) (机械装备先进制造河南省协同创新中心 河南 洛阳 471003)

0 引 言

最近几年，人们对智能化生活的需求日益增强，发展方便、舒适、灵活的交互方式成为研究人员的迫切要求。以人类手部为基础的手势语言具有直观、自然、丰富的特点，符合人类的交流习惯，手势识别正引起国内外研究学者的关注。对于手势识别，提取手势特征是手势识别算法的重要组成部分。

杨纪争等[1]从手势边缘序列角度出发，建立跟随空间变化的时空域边缘序列，并根据计算递归图像之间的距离完成手势识别。Ren等[2]利用轮廓梯度多尺度加权直方图进行手势方向的计算，并使用轮廓点的位置与方向进行特征提取，利用支持向量机进行手势识别。Zhou等[3]从手势图像中提取边缘，通过并行边缘特征提取手势轮廓突出的边缘点，并以手腕位置为中心，提取手的位置、方向进行手势识别。文芳等[4]提取手势轮廓的圆形度、凸包点以及缺陷点等信息构建特征向量进行手势识别。高晨等[5]提出一基于轮廓凸包检测指尖的算法，并将指尖数目、相邻两个指尖夹角等作为特征向量进行手势识别。上述文献是在手势轮廓的基础上运用相应的算法进行手势识别。虽然这些算法的运算量较小，算法结构不复杂，具有一定的实用性，但是手势轮廓所包含的信息有限，较难为手势识别提供更多有效的特征，不便进一步提升算法的性能，具有一定的局限性。

除了利用手势轮廓信息构建特征外，还有研究学者使用手势的二值图像进行特征提取。蒲兴成等[6]利用手势二值图像的 Hu不变矩以及手指个数作为特征向量，使用支持向量机进行手势识别。Chevtchenko等[7]对手势二值图像采用傅立叶描绘子、Zernike矩、伪Zernike矩、Hu矩、复数矩构建特征向量，采用多层感知器神经网络进行分类识别。曹雏清等[8]利用深度传感器的数据分割出手势，并提取手势二值图中包含的手指数量、手指间的夹角作为特征向量进行手势识别。刘淑萍等[9]利用形态学处理消除手掌区域，通过计算连通域个数检测手指数量，并结合手势图像的HOG特征进行手势识别。屈燕琴等[10]利用手势二值图像提取手指弧度、指间弧度、手指数目等组建特征向量进行手势识别。杨学文等[11]利用重心与边缘确定手势主要方向，并建立手势直角坐标系提取空间特征，使用手势坐标点分布特征以及距离模板进行手势识别。曹杰等[12]利用曲率提取手势中指尖位置，并结合二值图像的Hu不变矩进行手势识别。上述文献多利用手势二值图像的表观特征进行手势识别。虽然这些算法提取的手势特征结合相应的识别算法在识别率上取得一定的效果，但仍存在一些不足需要进一步改进，如算法结构复杂，实时性和鲁棒性不高等。

除了上述利用轮廓、二值图像提取手势特征外，机器学习中的一些网络模型可以从图像中自动提取相应的手势特征。王龙等[13]利用卷积神经网络自动提取手势图像的特征进行手势的分类与识别。吴晓凤等[14]利用改进的卷积神经网络Faster R-CNN对手势图像进行特征提取以及识别分类。Gomez-Donoso等[15]使用卷积神经网络估计手势图像中手部的关节点位置，并利用关节信息预测手势的类别。蒋穗峰等[16]利用稀疏自编码器提取手势图像的特征，并利用softmax分类器进行手势识别。陶美平等[17]将手势图像分块后训练稀疏自动编码器获取手势的边缘特征，并使用该特征利用分类器进行手势识别。上述文献虽然算法复杂程度较低，但算法的针对性不强，平均识别率不高，还需诸多改进来满足手势识别的要求。

目前手势识别算法多利用轮廓、二值图像等提取相应特征，虽然取得了诸多进展，但是在特征提取过程中丢失较多手势的纹理信息，如边缘轮廓细节、手掌纹路、肌肉凸凹区域、手指关节表面细节等。因此本文从手势灰度图像的纹理含有丰富的手势类别信息的角度出发，提出一种基于GLCM和Gabor小波变换的手势纹理特征的手势识别方法。该方法首先通过构造多方向共生矩阵和Gabor滤波器来提取手势纹理的GLCM特征和Gabor特征；其次将所提取的两种纹理特征归一化后串联构建手势纹理特征向量；最后，利用深度堆栈自编码网络对所构建的手势纹理特征向量进行学习与识别，进一步提高手势识别方法的泛化能力。本文算法的流程图如图1所示。

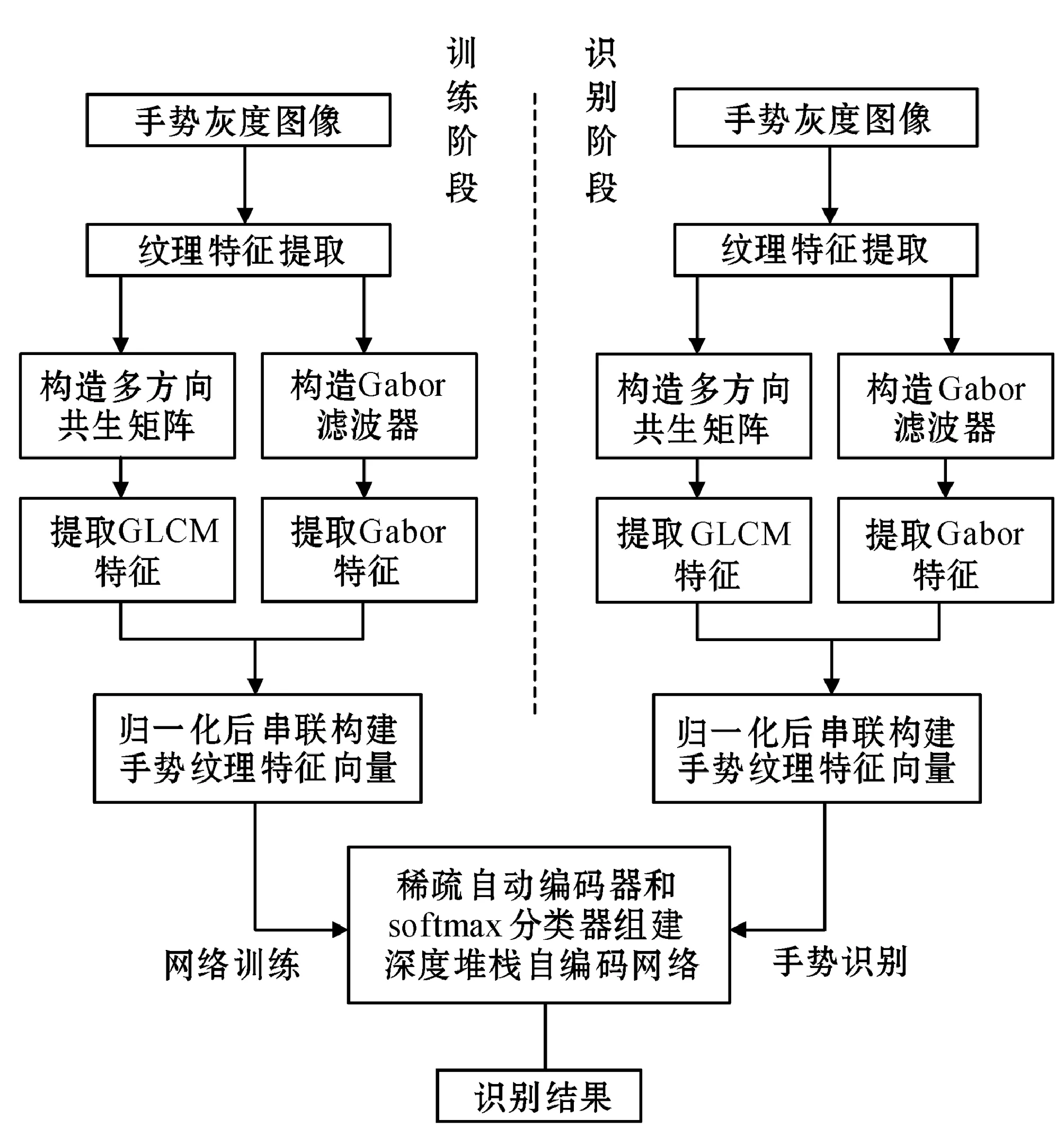
图1 本文算法流程图

1 手势纹理特征提取

如图2所示，手势的灰度图像蕴含大量的纹理信息，其中不仅包含现有手势识别常用的边缘轮廓细节信息等，还蕴含人手的表面纹路、手指关节表面细节等类别信息。针对手势纹理的特点，基于像素灰度统计的共生矩阵对纹理的局部变化特点，如像素点之间的变化幅度、相互关联等，有较好的表征能力；而Gabor小波变换通过Gabor滤波函数对手势灰度图像进行卷积运算，可以得到其不同频率、尺度、方向的纹理信息，对整体纹理的变化有较强的描述能力。因此，为了充分利用手势灰度图像中的纹理信息，提高所提取特征的有效性，本文提取手势纹理的GLCM特征和Gabor特征构建手势纹理特征向量。首先构建多方向共生矩阵统计手势灰度图像中两个像素灰度级之间的联合分布，并提取共生矩阵的角二阶矩、对比度、相关性、熵以及逆差矩作为手势纹理的GLCM特征；其次，构建Gabor滤波器对手势灰度图像进行Gabor小波变换，提取不同频率、方向的Gabor小波系数作为手势纹理的Gabor特征；最后分别将提取到的GLCM特征和Gabor特征进行归一化后串联构建本文的手势纹理特征向量。

图2 典型手势的灰度图像

1.1 手势纹理的GLCM特征

1.1.1多方向共生矩阵的构建

共生矩阵通过统计手势灰度图像中灰度为a和b的像素对满足某一方向位置关系次数来表征纹理分布。图像中像素对的位置关系越多，所构建的共生矩阵数量就越多，对手势纹理的描述就越丰富。因此本文首先建立像素对多个方向的位置关系，以达到提取多个共生矩阵的目的。

设Q代表中心像素点与其圆形邻域边界上像素点所有方向的位置关系，规定中心像素点水平向右为该圆形邻域的0°方向，且像素对位置关系的指向是从中心像素点至圆形邻域边界上的像素点。若以圆形邻域的0°方向为起始位置，以角度θ为间隔在圆形邻域中建立像素对位置关系，那么中心像素点与其圆形邻域边界上的像素点一共存在360°/θ个方向的位置关系，即Q∈ [ 0°,θ,2θ,…，kθ]，kθ=360°-θ。图3为中心像素点与其圆形邻域边界上像素点所有方向的位置关系示意图，其中圆形邻域半径r=3，间隔角度θ=45°，从而形成8个方向的位置关系。通过调整圆形邻域半径r与间隔角度θ可以形成多种不同的像素对位置关系，进而统计生成相应的共生矩阵。

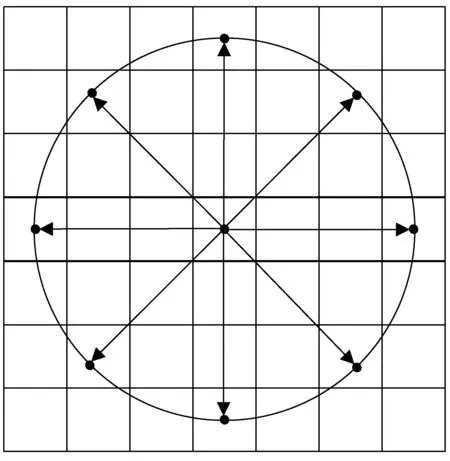
图3 圆形邻域中的位置关系

假设一幅手势图像f拥有L个灰度级，G代表一个矩阵，则矩阵中元素gi,j的值是中心像素点灰度值为zi和其圆形邻域边界上像素点灰度值为zj的像素对在图像f中符合某一方向位置关系的总次数，其中1≤i,j≤L，按此方法统计所形成的矩阵为该方向位置关系的共生矩阵。

图4为共生矩阵生成过程。以图4(a)中灰度图像统计生成0°方向位置关系共生矩阵的过程为例。首先按上述形成位置关系Q的方法构建圆形邻域0°方向的位置关系，位置关系的指向是从中心像素点至圆形邻域边界上0°方向的像素点，为方便示例圆形邻域的半径r=1。

(a) 灰度图像 (b) 共生矩阵图4 共生矩阵生成过程

然后遍历图4(a)中的灰度图像，统计所有中心像素点灰度值为zi和其圆形邻域边界上像素点灰度值为zj的像素对符合0°方向位置关系的总次数，并将其值赋予共生矩阵中的元素gi,j。当共生矩阵中所有元素均统计完毕时，即可得到0°方向位置关系的共生矩阵。例如在图4(a)中所有中心像素点灰度值为1和其圆形邻域边界上像素点灰度值为2的像素对符合0°位置关系的总次数为2，图中的实线箭头为图5中圆形邻域0°方向位置关系的简化表示，则图4(b)中共生矩阵元素g12的值为2。其他方向位置关系共生矩阵的生成方法与0°方向位置关系共生矩阵的方法相同，只是统计时所使用位置关系的方向不同。

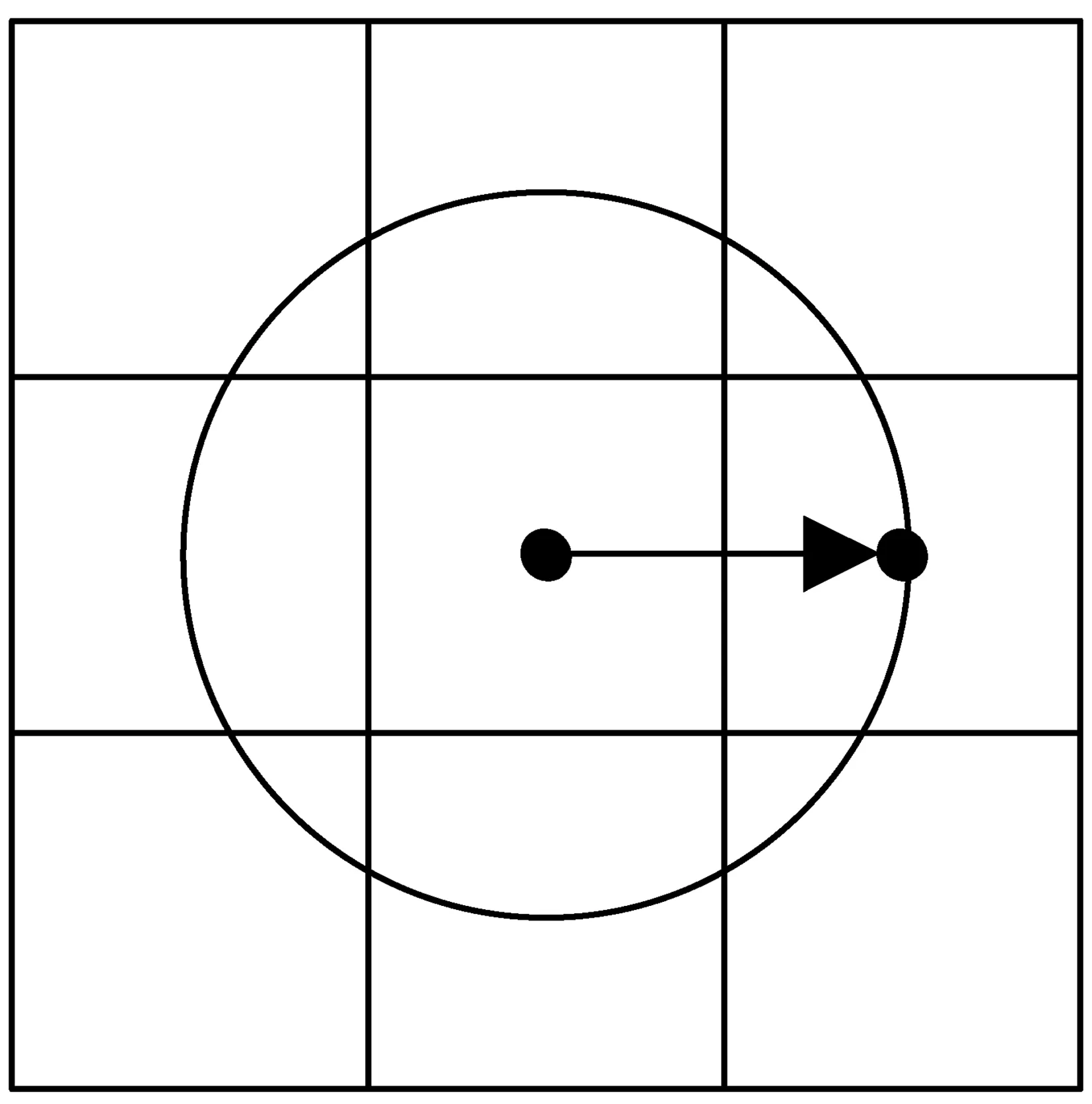
图5 圆形邻域中的0°方向位置关系

根据本文建立的位置关系可以生成360°/θ个共生矩阵，从而可以使共生矩阵能够统计多个方向的手势灰度纹理。另外从共生矩阵的生成方法可知所生成矩阵大小与手势图像f的灰度级相关，为L×L。而手势图像的灰度级数较大，在统计共生矩阵时较大幅度的增加算法的运算量。因此，在使用手势灰度图像统计多个方向的共生矩阵前，先对手势灰度图像进行灰度级数缩减处理，减小算法运算量，公式如下：

(1)

式中：f(x,y)为原手势灰度图像，f′(x,y)为灰度级缩减后的灰度图像，n为缩减后灰度级数。最终可以统计得到360°/θ个n×n大小的共生矩阵。

1.1.2手势纹理GLCM特征的构建

通过本文共生矩阵的构造方法，可以得到手势图像中多个方向的纹理分布特点。为了对这些纹理分布特点进行有效的表征，本文计算所有方向共生矩阵的角二阶矩、对比度、相关性、熵、逆差矩五个特征参数作为手势纹理的GLCM特征，从而达到描述手势纹理分布特点的目的，公式如下所示：

角二阶矩W1：

(2)

对比度W2：

(3)

(4)

(5)

(6)

(7)

(8)

熵W4：

(9)

逆差矩W5：

(10)

式中：G为共生矩阵，n为共生矩阵的阶数，u1、u2、δ1、δ2为式(4)中的过渡参数。从而构建5×360°/θ维的手势纹理的GLCM特征：

式中：多个共生矩阵的特征参数按其统计时所对应位置关系方向的大小排列。

1.2 手势纹理的Gabor特征

1.2.1Gabor滤波器的构建

二维Gabor小波变换可以提取图像不同频率尺度和方向的纹理信息。Gabor小波变换是利用滤波器与图像进行卷积运算将原始图像转换到频域空间，滤波器的表达式为：

(11)

(12)

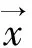
(13)

(14)

从上述Gabor滤波器的表达式可知，Gabor滤波函数受参数φμ、kν和σ的影响。通过调整参数φμ、kν和σ即可得到不同方向、频带、大小的Gabor滤波器，然后利用得到滤波器对图像进行Gabor小波变换的处理，从而获取图像中每个像素点所对应的Gabor小波系数。对图像的Gabor变换可以用与图像卷积来表达：

有些美索不达米亚文化相信，众神甚至会不时牺牲自己或彼此，以确保宇宙持续存在，人类继续生存。例如玛雅人相信，玉米是众神的肉，含有神圣的力量，在收获的时节，众神其实是牺牲自己来养活人类。当人类进食时，这种神圣的力量便传入人体内，特别集中于血液，杀害活人以作祭品，是回报这个恩惠，并让神圣力量回归众神的一种方式。食物和熏香也被当作供品呈现，但人祭(human sacrifice)仍被认为是最重要的祭品。

(15)

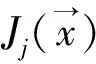
1.2.2手势纹理Gabor特征的构建

对灰度图像进行Gabor小波变换后可以得到所有像素点对应的Gabor小波系数。而对于一幅手势灰度图像，其中位置较邻近的像素点所对应的Gabor小波系数相似，可以使用一点的小波系数代替周围的像素点。如图6所示，在手势灰度图像中选取若干均匀分布的离散像素点，并将灰度图像划分为与离散像素点相对应的若干邻域，划分数量记为n。在对离散位置像素点进行Gabor小波变换时，滤波器窗口σ的大小与离散位置像素点的邻域大小相同。在利用式(15)进行卷积运算时，Gabor滤波器不再遍历整个图像，而是只与n个离散像素点对应的邻域进行卷积运算，从而得到离散像素的Gabor小波系数Fi，i∈[1,2,…，n]。提取所有离散位置像素点的Gabor小波系数，即可得到m×n个Gabor小波系数，m为所构建的滤波器个数，并将这些Gabor小波系数作为手势纹理的Gabor特征。

图6 离散像素示意图

本文所选取的Gabor滤波器参数如下：kv=π/4,π/2，φμ=0,π/4,π/2,3π/4，σ与离散点邻域的大小相同，从而可以得到8个Gabor滤波器，如图7所示。经过离散像素位置Gabor计算后，最终提取到8×n维的手势纹理的Gabor特征：

式中：上标对应不同的Gabor滤波器，下标对应所选取的离散位置像素点的标号。

图7 Gabor滤波器

1.3 手势纹理特征的构建

由于所提取的两种纹理特征的数量级不同，因此先对提取到的GLCM特征和Gabor特征分别进行归一化处理，公式如下所示：

(16)

式中:xi为特征向量中的第i个特征值，yi为归一化后的结果。设α′、β′分别表示归一化后的GLCM特征和Gabor特征，并将两者串联组成本文的手势纹理特征量γ=[α′,β′]，共178维，其中手势纹理的GLCM特征50维，Gabor特征128维。

2 手势识别

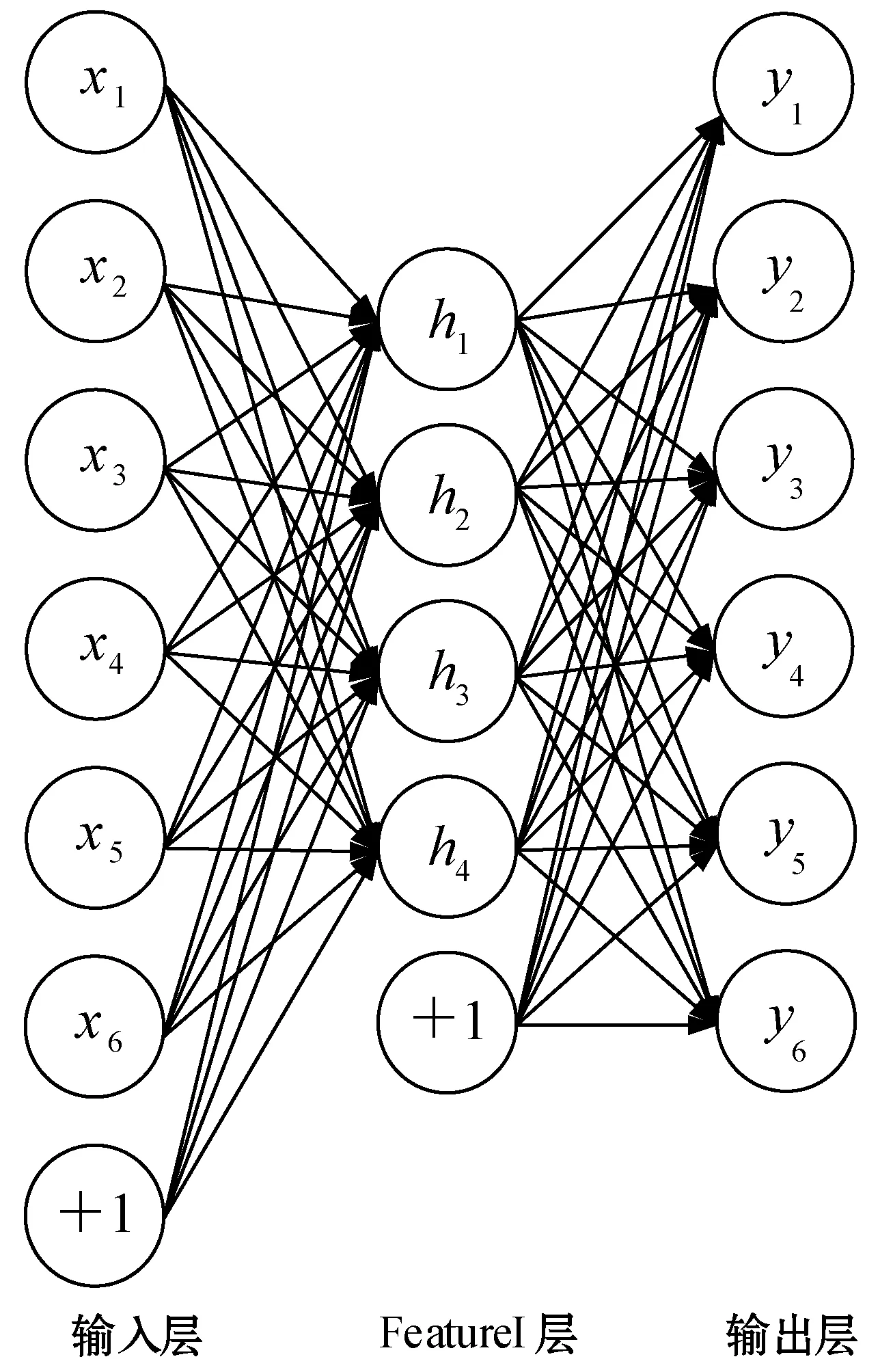
本文手势纹理特征向量中包含两种不同表征意义的纹理特征量，为了更加有效地进行手势的分类与识别，本文利用机器学习理论中的稀疏自动编码器与softmax分类器组建深度堆栈自编码网络进行手势识别。深度堆栈自编码网络共四层，分别为输入层、两层稀疏编码器以及softmax分类器， 如图8所示，图中+1节点为该层的偏置项。深度堆栈自编码网络的层数和节点数远远多于传统神经网络，通过采用逐层训练的预训练方法，加快了网络的收敛速度并避免陷入局部最优解，使其可以通过输入特征数据形成具有更加抽象、高级的特征，从而发现输入数据的分布式特征表征，到达有效学习输入特征数据的目的。其中稀疏自动编码器为3 层神经元结构，输入层的节点数与输出层节点数相等，隐含层节点数少于输入层的节点数，如图9(a)所示，其通过学习一个恒等函数，使输出层的目标值接近于输入层的输入值，从而获得输入特征数据的相关性和压缩表示。而softmax分类器则利用softmax回归模型将经过两层稀疏自动编码处理的输入特征数据进行分类，从而完成本文纹理特征的识别分类。

本文网络的数据传递过程如下，首先将提取的特征数据输入第一层稀疏自动编码器，可以得到输入数据在FeatureI层的特征表征数据，如图9(a)所示；然后将FeatureI层的特征表征数据作为第二层稀疏自动编码器的输入，可以得到FeatureII层的特征表征数据，如图9(b)所示；最后将FeatureII层的特征表征数据作为softmax分类器的输入，如图9(c)所示，从而完成网络的数据传递。

图8 深度堆栈自编码网络结构

(a) 第一层编码器

(b) 第二层编码器

(c) softmax分类器图9 网络数据的传递过程

本文利用逐层训练的方法对深度堆栈自编码网络进行预训练，过程如下：首先输入手势纹理特征向量训练网络中的第一层稀疏自动编码器，当训练完成后可以得到FeatureI层的一阶特征数据；其次输入该一阶特征数据训练第二层稀疏自动编码器，当训练完成后可以得到FeatureII层的二阶特征数据；然后输入该二阶特征数据训练softmax分类器，从而完成网络的预训练过程。当所有层训练完毕，对整体网络进行微调，从而完成对深度堆栈自编码网络的训练。通过微调可以大幅提升网络的性能表现，首先将网络的所有层视为一个模型，在每一次迭代中优化整体网络中所有的连接权重以及偏值项。

3 实验结果及分析

为验证本文手势方法的有效性，利用手势样本提取特征进行实验。本文数据库包含15种手势，每种手势200幅图像，如图10所示，并从1到15进行编号。其中从本文数据库中挑选800个手势图像作为训练数据，1 200个作为识别数据。

图10 本文手势种类

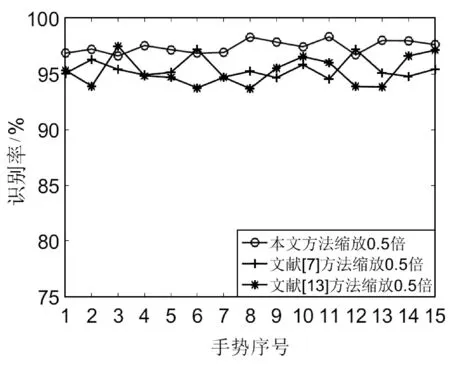
图11为本文、文献[7]以及文献[13]的实验结果。图12为将数据库中的样本分别旋转-20°、-10°、10°、20°后本文、文献[7]以及文献[13]的实验结果。图13为将数据库中的样本分别缩放0.5、0.75、1.25、1.5倍后本文、文献[7]以及文献[13]的实验结果。图中横坐标为手势序号，纵坐标为相应的序号的识别率。为验证识别率的稳定性，采用各个手势识别率的标准差作为参考，手势识别实验结果的对比如表1所示。

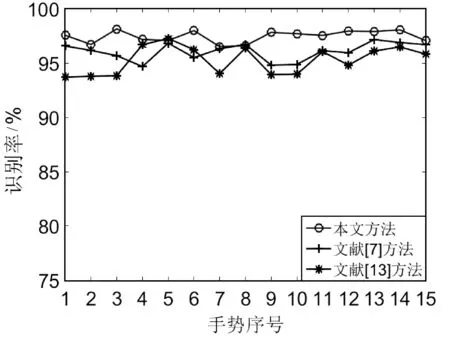
图11 手势识别结果

(a) 旋转-20度

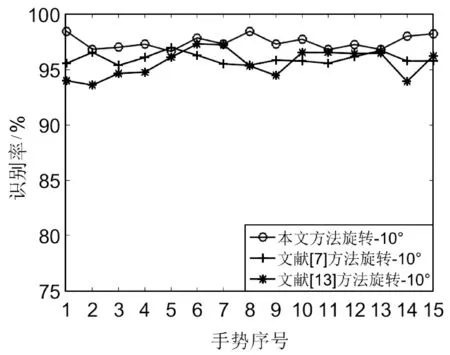
(b) 旋转-10度

(c) 旋转10度

(d) 旋转20度图12 旋转后手势识别结果

(a) 缩放0.5倍

(b) 缩放0.75倍

(c) 缩放1.25倍

(d) 缩放1.5倍图13 缩放后手势识别结果

图像类别参数类型手势识别方法本文文献[7]文献[13]原始图像平均识别率97.4%95.8%94.5%识别率标准差0.590.650.88旋转-20°处理平均识别率96.8%95.1%94.4%识别率标准差0.570.790.84旋转-10°处理平均识别率96.9%95.7%94.9%识别率标准差0.550.730.86旋转10°处理平均识别率97.1%96.1%94.7%识别率标准差0.590.700.79旋转20°处理平均识别率96.8%95.5%95.1%识别率标准差0.611.070.85缩放0.5处理平均识别率97.0%95.7%95.3%识别率标准差0.650.860.72缩放0.75处理平均识别率96.8%95.5%94.8%识别率标准差0.600.740.90缩放1.25处理平均识别率97.1%95.7%94.3%识别率标准差0.610.940.76缩放1.5处理平均识别率96.9%95.6%94.0%识别率标准差0.540.820.93

从上述对比实验的结果可知，本文方法的平均识别率高于文献[7]以及文献[13]的方法，且识别率的标准差最小。在不同旋转角度下以及缩放尺度下，依然保持较高的识别率，对于所有手势种类而言十分稳定，具有良好的旋转不变性以及缩放不变性，从而也验证了本文手势识别方法的稳定性和准确性。

4 结 语

本文利用手势灰度图像的纹理含有丰富的手势类别信息的特点，提出一种基于共生矩阵和Gabor小波变换的手势纹理特征提取方法。首先，构建多方向共生矩阵提取手势纹理的GLCM特征；其次，通过在手势灰度图像的Gabor小波变换提取手势纹理的Gabor特征；然后通过归一化处理将两种特征串联构建手势纹理特征，并利用稀疏自动编码器和softmax分类组成的深度堆栈自编码网络进行手势识别。实验表明，本文方法有效可行，对15种手势的平均识别率为97.4%。但是本文的特征提取方法对手势图像中纹理信息的利用仍然不够充分，还有待提升。因此下一步工作是优化本文的特征提取方法，使其能够最大程度地利用手势纹理信息，从而进一步提高识别的准确率以及对各种类型的手势图像的适应性。