基于可编程电路的低延时中值求取方法
2019-07-15李宗凌汪路元禹霁阳牛跃华张伟功
李宗凌 汪路元 禹霁阳 李 珂 牛跃华 张伟功
1(中国空间技术研究院北京空间飞行器总体设计部 北京 100094)2(首都师范大学信息工程学院 北京 100048)
0 引 言
中值求取是数字雷达信号处理和图像处理过程的基本方法,它在实际应用中能够实现诸如中值滤波等功能,是一种经典的平滑噪声的方法。国内外学者一直致力于快速实现中值求取的研究,而可编程电路具有并行计算的特点,用其实现排序算法能极大提高运算速度,适合于雷达信号处理和图像处理等实时性要求较高的场合。
中值求取是一种点处理方法,处理时间与实现手段及序列长度等因素有关。为此,出现了许多快速求取中值方法,常见的方法类别有:(1) 基于软件实现的改进方法:采用排序思想,优化排序算法,减少排序运算量[1-2]。此类方法主要应用于基于处理器实现的软件,无法满足图像或雷达信号处理等高实时性应用领域的需求。(2) 中值求取算法改进方法:包含选点法[3]、近似法[4]、均值法[5]、方差法[6]等。此类方法通过近似计算思路,改进中值求取算法,在牺牲一定精度性能的基础上,较大幅度地减少数据处理量,从而达到快速求取中值的目的,但此类方法具有一定局限性,只限于某些特定场合应用,通用性较差。(3) 并行计算方法:主要采用FPGA等可编程电路构建并行处理单元,用以加速求取中值[7-10]。此类方法主要利用FPGA等器件的特点,构建流水处理架构,可快速实现中值滤波等信息处理算法。流水处理的好处显而易见,然而,却少有人考虑流水延时对高速实时信号处理带来的影响;与此同时,构建流水线处理过程中,复杂的逻辑控制也成为一个不可忽视的问题。
针对上述情况,本文提出了一种基于可编程电路的快速中值求取方法,充分利用FPGA等可编程电路全并行流水处理、硬件资源易扩展、并行计算能力强等特点,实现了通过简单逻辑控制实现低延时求取中值的目标。
1 算法原理
1.1 传统中值求取算法
传统中值求取算法通过快速排序寻找序列的中值,该方法对序列长度、数值没有限制,具有更加广泛的运用范围,因此选择传统算法作为低延时中值求取算法的对照研究。由算法原理可知,传统中值求取算法的执行效率由快速排序算法的时间复杂度决定,其基本思想是通过每次排序将序列划分为相互独立的两个子集合,其中一个子集合中所有数值都比另一个子集合中所有数值小,然后分别对这两个子集合继续进行排序,直到滤波窗口中所有像素点有序。传统中值算法最后选取位于序列中间位置的元素作为中值的输出。
1.2 低延时中值求取算法
x(n)是长度为N的原始数据序列,其中,n=0,1,…,N-1;对x(n)序列的每个数据进行位移和偏移处理,获得N个位移和偏移处理后的数据xb(n),具体为:xb(n)=x(n)·2m+n,其中,n=0,1,…,N-1,m=INT{log2(2N-1)}。由上述变换方法可知,xb(n)序列中任意两个值不相等。
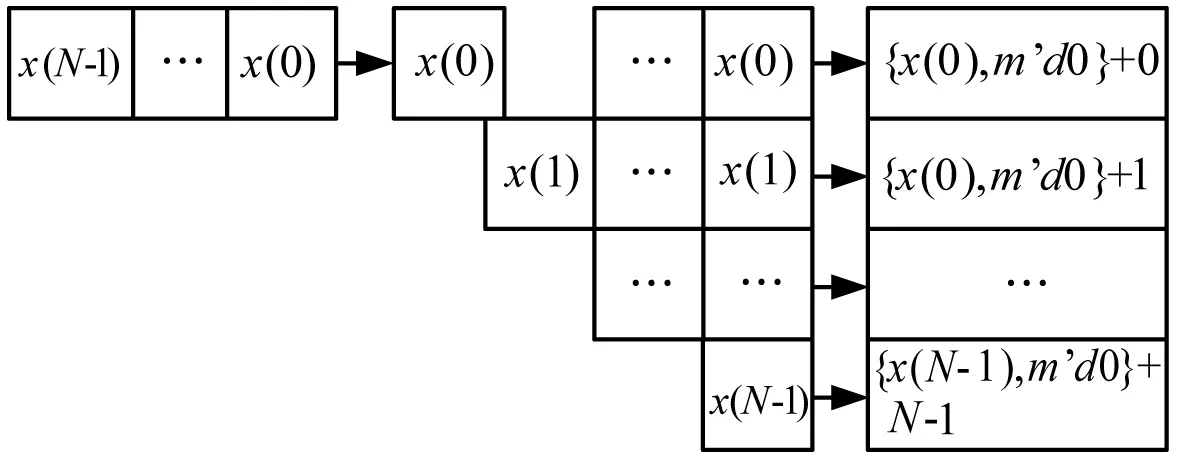
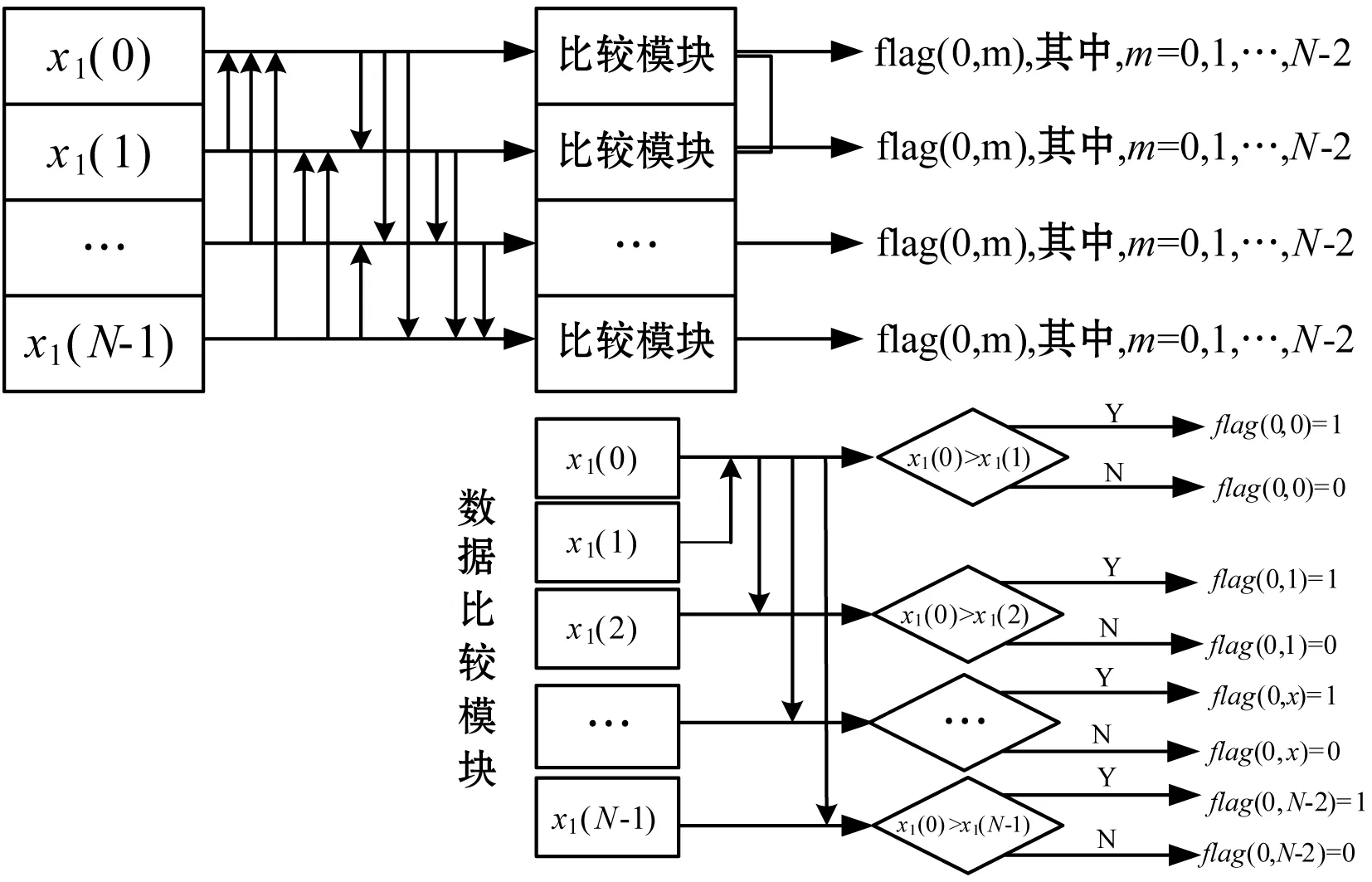
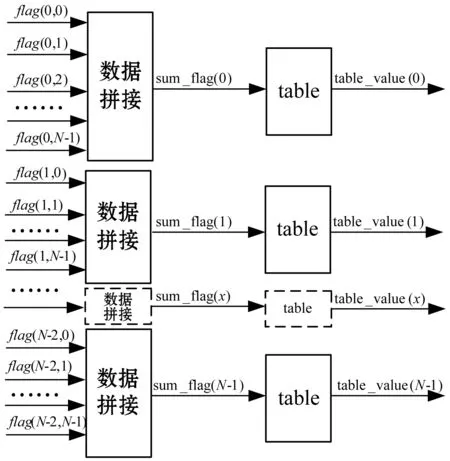
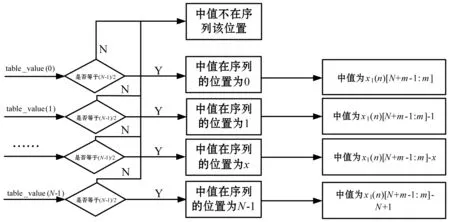
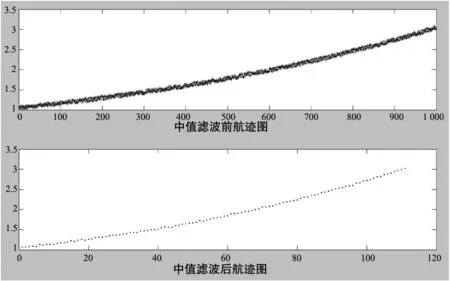
将每个位移和偏移处理后的数据依次和其余N-1个数据比较大小,获得每个数据的N-1个比较结果的布尔值,比较结果的布尔值flag(p,q)具体为:当p>q时,flag(p,q)=1;当p 将每个数据比较值为1的个数值与(N-1)/2进行比较,确定等于(N-1)/2数据比较值为1的个数值所在变换后序列的位置。获得变换后序列的数据进行位移和偏移的逆处理,即获得原始数据序列x(n)的中值结果。位移和偏移逆处理方法为:x(n)=(xb(n)-n)/2m,其中,m=INT{log2(2N-1)},n=0,1,…,N-1。 由上可知,传统中值求取方法基于排序的思想,存在循环迭代结构和计算次数不确定的缺陷,耗时长,而且受限于计算架构,并行度低,硬件加速效率低,无法发挥FPGA等可编程逻辑电路的全并行优势,使得求取中值的流水延时过长,无法实现快速获取中值。本文设计的中值求取方法克服了以上缺点,提供了一种基于并行计算思想的中值求取方法,充分利用FPGA等可编程电路全并行流水处理、硬件资源易扩展等特点,解决了数据序列低延时中值求取问题。 如图1所示,将长度为N的原始数据序列的数据分别通过寄存器缓存,使数据完全同步,然后进行变换处理,使数据互为不相等。序列长度为N的原始数据序列的数据x(n),经过N-1级寄存器寄存处理后,N个数据处理成完全并行同步,同时对寄存在寄存器中的每个数据进行变换处理,得到新的数据xb(n)=x(n)·2m+n,其中,m=INT{log2(2N-1)},n=0,1,…,N-1,通过上述处理,保证了寄存在寄存器中的每个数据变量完全不相等。 图1 变换处理 如图2所示,变换处理完成后,让并行数据xb(n)中各个数据变量相互比较。以每个输入数据为比较基准,得到相应的布尔比较值。需要注意,各个数据变量是同时进行相互比较,以自身为基准同时得到相应的布尔比较值flag(n,m),其中,n=0,1,…,N-1;m=0,1,…,N-2。 图2 序列比较 如图3所示,将并行比较处理后所有的布尔比较值flag(n,m)进行位拼接,其中,n=0,1,…,N-1;m=0,1,…,N-2。拼接得到N-2个位宽N-1的数据sum_flag(n)={flag(0,n),flag(1,n),flag(2,n),…,flag(m,n)},其中,n=0,1,…,N-1;m=0,1,…,N-2。利用sum_flag(n)为输入,分别进行查表得到数值table_value(n),其中,n=0,1,…,N-1。其中,查找表的位宽为m、深度为2N-1、查找表的值等于该地址中比特位为1的数量。 图3 数据拼接及查找表 如图4所示,将所有查表结果table_value(n)同时与数值(N-1)/2进行比较,若table_value(n)=(N-1)/2,则该值对应的n即为中值所在原数据序列中的位置,其中,n=0,1,…,N-1。通过中值所在位置可得到数据长度为N的数据序列的中值median_value=x1(n)[N+m-1:m]-n,其中,m=INT{log2(2N-1)},n为中值在序列的位置,将其向外输出。 图4 中值求取 当数据序列较大时,如5×5窗口中值求取运算中,如果按文中设计方法,则查找表大小将设计深度为224,硬件资源显然占有过多。通过分析运算特点,可采用分段查表的方法解决该问题,可将比较结果分为3段,每段位宽为8,此时只需要3个深度为256的查找表,再通过一个加法器将3个查找表结果相加即解决该问题,相应流水延时也只是增加1个时钟周期。 中值求取广泛应用于雷达目标探测及光学图像处理方面。如在雷达信号处理中,中值求取可应用到探测目标航迹关联、处理结果平滑等方面;在光学图像处理中,中值求取可应用到图像去噪、目标检测与识别等方面。图5-图6为基于本文方法实现的求取中值的处理效果。 图5 雷达信号处理方向应用 将本文设计的中值求取方法利用硬件语言Verilog实现,分为3×3和5×5两种窗口规格,并将其布置在Xilinx公司可编程器件K7-325T上,得到相应的硬件资源占用情况,并与参考文献中相关实现方法对比。具体如表1所示。 通过表1可知,本文方法在占用硬件资源方面相比参考文献多一些。但是,在流水延时方面,本文方法优势较为明显,在3×3窗口时,流水延时是参考文献[8]的50%;在5×5窗口时,流水延时仅为参考文献[9]的37.5%。通过进一步比较分析,虽然比较次数等方面没有优势,但是本文方法在利用可编程电路实现过程相比参考文献简单,通过采用较多比较逻辑资源,达到简化流程控制的目的,同时,大大缩短了流水处理延时,最终的硬件资源综合占用率和时序也相应得到优化。随着微电子技术的发展,本文方法占有的硬件资源相比大规模高性能FPGA完全可以接受。因此,本文设计的低延时高性能中值求取方法相比以前的方法优势明显。 本文利用FPGA等可编程逻辑电路全并行流水处理、易于硬件资源扩展和复用的特点,设计了一种快速求取数据序列中值的方法。该中值求取方法完全摒弃传统采用排序思想求中值的思路,创造性的采用可编程电路的逻辑和存储资源搭建处理架构,提升了并行计算能力。 利用FPGA等可编程电路丰富的逻辑运算和存储单元,便于快速实现移位、截取、拼接和构建查找表的特点,采用逻辑单元搭建全并行比较器,快速得到序列中各数的相互比较结果布尔值;通过位拼接操作将其组合成数据结果;采用存储单元构建比较结果查找表,通过判定查表结果得到序列中值在变换后的序列位置。上述方法避免了大量加法运算,提升了处理效率,有效减少了流水延时。 FPGA等可编程电路在上述处理过程采用全并行流水处理架构,极大增强了数据处理速率和效率,简化了逻辑控制流程,从而能够实现低延时求取数据序列的中值。在保证电路稳定性和可靠性的前提下,流水延时可控制在两个处理时钟,大大优于当前业内相关方法。1.3 算法比较
2 结果与分析
2.1 可编程电路实现
2.2 处理效果
2.3 性能分析
3 结 语
