波形钢腹板组合曲线箱梁的挠度偏载系数分析∗

丁汉山 蒋勇

(东南大学土木工程学院 南京211189)

引言

波形钢腹板箱梁桥是20 世纪末出现的一种新型的钢-混组合结构桥梁,因其具有较好的受力性能及便于运输安装等优点,在我国钢结构桥梁建设中占据重要地位。与混凝土曲线梁桥相比,用波形钢板替代混凝土腹板,降低了结构自重,提高了腹板的抗剪性能及结构耐久性[1-4]。对于波形钢腹板曲线箱梁因腹板厚度较薄,由钢腹板剪切效应产生的挠度变形较混凝土箱梁将增大10% ～30%左右[5],同时在弯扭耦合作用下,箱梁在偏载作用下产生的挠度变形也会更加明显[6]。

对于薄壁箱梁的挠度计算,国内外已有学者进行过相关研究。Taniguchi 在叠合梁理论上推导出波形钢腹板组合梁的挠度计算公式[7]。Kato.H等引入两个独立的位移函数建立截面平衡方程,得到了波形钢腹板组合梁的挠度计算公式[8],利用矩阵位移法求解扩大了理论的应用范围。国内陈玉骥、罗旗帜等人根据薄壁曲线梁理论和势能变分原理,推导出薄壁曲线箱梁在弯、扭、剪力滞耦合时的曲线箱梁几何非线性控制微分方程,再采用同伦延拓法可求得结构在荷载作用下的半解析解[9]。甘亚南、周广春以薄壁曲杆理论为基础,提出一种对曲线梯形箱梁静力学特性准确分析的解析法,提高了该类结构应力和挠度计算精度[10]。

目前,对于曲线箱梁在荷载作用下挠度变形的研究,腹板多采用混凝土浇筑,对于波形钢腹板曲线箱梁的偏载挠度研究鲜有报道。为此,本文以薄壁曲线梁理论和能量变分原理为基础,推导曲线箱梁桥的变形控制微分方程,并设计3 片试验曲梁,验证曲线箱梁桥偏载理论模型的正确性,对波形钢腹板组合曲线箱梁的设计计算提供参考。

1 波形钢腹板曲线箱梁受力分析

对波形钢腹板组合曲线箱梁进行受力分析时,可采用曲杆结构力学及薄壁箱梁理论分析其受力性能,揭示作用力传递机理及各因素之间的影响关系。

图1 为实际工程中应用最广的单箱单室波形钢腹板组合曲线梁截面结构。z、y、x为通过截面形心轴向、竖向和径向坐标;hc为波形钢腹板高度;tw为波形钢腹板厚度。假定混凝土箱梁顶底板竖向纤维间无相互挤压,忽略混凝土顶底板平面外的剪应变及横向正应变,波形钢腹板与混凝土顶底板在弹性阶段时不产生相对滑移,剪力全部由波形钢腹板承担。

从力学角度分析,结构在荷载作用下的弹性位移由弯曲变形、轴向拉伸和剪切变形组成,在传统混凝土曲线梁桥中腹板剪切变形产生挠度较小,一般可忽略不计。对于波形钢腹板曲线组合箱梁,钢腹板抗剪面积较小,腹板产生的剪切应变能不可忽略。

为求出波形钢腹板剪切应变能,在纵向位移函数中引入剪应变函数,见式(1),假定腹板剪应力沿高度方向均匀分布,则腹板位置任意微元体剪应变方程可表示为：

式中：Q(x)为波形钢腹板的竖向剪力;Aw为波形钢腹板截面面积;k为剪切形状系数;Ge为波形钢腹的有效剪切模量,根据Johnson R P 等[11]试验证明,其计算公式可表示为：

式中：b和d分别为波形钢腹板的水平板宽和斜板宽;α为波形钢板的折叠角;G为钢板的剪切模型。

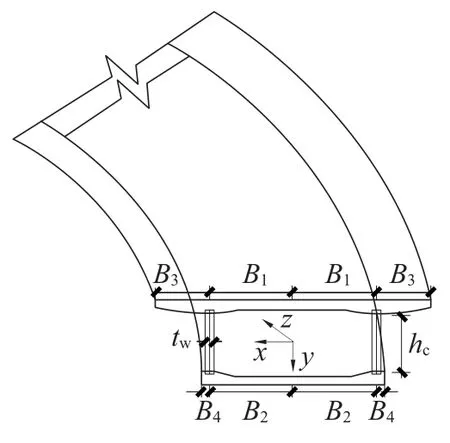
图1 波形钢腹板箱梁截面Fig.1 Section of box girder with corrugated steel webs

则波形钢腹板的剪切应变能为：

式中：V为波形钢板的微段体积;z为波形钢板轴向长度;As为波形钢腹板的面积。

在偏载作用下箱梁空间应力分析较为复杂,当箱梁设置足够数量横隔板时,畸变变形可忽略不计,故计算薄壁箱梁横截面上任意点的应力时,考虑弯曲和扭转效应即可。

箱梁在发生纵向弯曲时,箱梁截面上将产生纵向弯曲正应力σM和纵向弯曲剪应力τM,如图2所示。

图2 箱梁纵向弯曲时截面应力图Fig.2 Stress diagram of section of box girder under longitudinal bending

箱梁的刚性扭转可分为自由扭转和约束扭转,箱梁自由扭转时,截面上纵向翘曲不受约束,因而截面上不产生纵向正应力,仅产生自由扭转剪应力τk,如图3a 所示; 当箱梁纵向变形受到约束,在截面上同时产生约束扭转正应力σω和约束扭转剪应力τω,见图3b、3c。

图3 箱梁刚性扭转时截面应力图Fig.3 Section stress diagram of box girder under rigid torsion

对于波形钢腹板曲线箱梁因弯扭耦合效应存在,在竖向荷载作用下箱形梁横截面和纵截面上应力为：

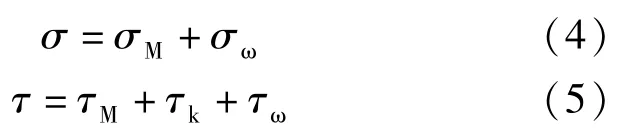
根据叶见曙等[12]波形钢腹板箱梁截面变形研究,截面纵向应变符合“拟平截面假定”,忽略钢腹板的弯曲应变能,则波形钢腹板组合曲线箱梁的弯曲应变能为：

式中：v″为截面的竖向位移引起的转角;γ′为波形钢腹板剪应变引起的转角;φ为截面绕剪切中心转角;EI为截面的抗弯刚度;R为曲线梁的曲率半径。

为了准确表达波形钢腹板曲线箱梁的翘曲位移,在符拉索夫采用截面扭角的一阶导数作为翘曲广义位移基础上,引入独立的扭转翘曲广义位移函数β,则曲线梁截面的翘曲位移表达为：

式中：v′为截面的竖向应变;γ为波形钢腹板剪应变;ω为广义扇形坐标。

任一微段截面翘曲正应力应变能为：

式中：Bω为截面翘曲双力矩;Iω为广义扇形惯性矩;β′为扭转翘曲广义转角的一阶导数。

波形钢腹板箱梁截面在扭转剪应力作用下,箱壁微元会发生图4 所示变形。其中,us表示箱梁壁厚中心线的环向坐标,uw表示形心轴曲线坐标。

图4 箱壁微元扭转变形Fig.4 Torsion deformation of box wall element

则曲线梁顶底板截面扭转剪应变γτ：

式中：ρ为截面扭转中心到箱壁上任一点切线的距离;φ′为截面扭转角在轴向的一阶导数。

波形钢腹板曲线梁约束扭转总应变能Uτ可由自由扭转应变能Us和约束扭转应变能Uw相加表示：

式中：Iρ为箱梁截面极惯性矩;Id为截面抗扭惯性矩。

式中：Ω为箱壁围成面积的2 倍;t为箱形截面的壁厚;A为箱壁所围的截面面积;s为箱梁截面周边位移的长度。

从而将波形钢腹板的弯曲应变能UM、腹板剪切应变能Uf、翘曲正应力应变能Uω及扭转剪应力应变能Uτ相加即可得到结构总应变能U：

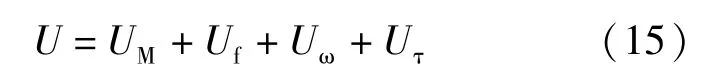
根据最小势能原理,当结构处于平衡状态时,系统总势能取极小值,一阶变分为零：

式中：V为外荷载势能;v为曲线箱梁在竖向荷载作用下位移;m为分布扭矩;q为梁纵向分布荷载。

波形钢腹板曲线箱梁的总势能为：

由最小势能原理可知δΠ =0,利用伽辽金法对式(18)进行泛函变分求解,即可求得波形钢腹板曲线箱梁变形分析的控制微分方程：

设各待求解位移及应变的函数为：

根据伽辽金法求解波形钢腹板曲线箱梁控制微分方程,即可得到箱梁各截面的应力及变形结果。

对于波形钢腹板曲线箱梁在竖向荷载作用下的内外侧挠度,可利用式(21)进行计算,即：

式中：vW表示试验梁外侧底板挠度;vN表示试验梁内侧底板挠度;B2示试验梁1/2 底板宽度。

2 试验验证

2.1 试验模型

为验证上述曲梁的挠度偏载理论,制作了3片波形钢腹板组合曲线梁,分别为试验梁L1 -2、L2 -2 和L2 -3。根据试验目的,除横隔板数量与腹板厚度不同外,试验梁顶底板尺寸及材料性能一致,见表1。

表1 试验梁参数Tab.1 Test beam parameter table

试验梁横截面尺寸如图5所示。试验梁为单跨等截面箱梁(单箱单室),全长为6600mm,计算跨径为6400mm,曲率半径为8000mm。实测材料性能参数： 钢纤维混凝土抗压强度平均值fck=26.8MPa,弹性模量Ec=32.5GPa; 试验梁钢筋均采用II 级带肋钢筋,腹板及中横隔板采用Q235钢板,弹性模量Es= 180GPa,泊松比为0.3,波形钢腹板剪切形状系数量k=1,有效剪切模量Ge=G/1.1。

图5 试验梁几何尺寸(单位： mm)Fig.5 Geometric dimensions of test beam (unit： mm)

波形钢腹板与混凝土顶底板结合部采用嵌入式剪力连接键,通过穿筋焊接于连接钢板,确保在试验荷载作用下腹板与混凝土顶底板无相对滑移产生。

为研究试验曲梁在偏心荷载作用下,底板内外侧挠度的变化规律,在试验梁的端支座、1/4L、1/2L、3/4L截面底板内外侧均布置电阻式位移计,测点布置如图6 所示。

图6 试验梁底板应变测点布置Fig.6 Strain measurement point layout of the bottom plate of the test beam

2.2 试验加载

试验梁加载采用千斤顶配合分配梁形式进行集中荷载的分级加载,加载方式可见图7a ～7c。

图7 试验装置布置图Fig.7 Arrangement of test beam equipment

由于文中挠度求解理论建立在材料线弹性基础上,为将试验实测值与理论值进行对比分析,文中加载工况分为弹性范围内跨中单点内侧、跨中单点外和跨中双点加载侧加载三种加载方式。

试验加载分5级加载,每级加载稳定读数2min后,记录对应实际荷载及挠度数据,具体试验布置和测试方案如图7d ～7e 所示。

3 试验及结果分析

采用有限元分析法对试验梁的加载工况进行完全仿真,利用ANSYS 建立试验梁整体式有限元模型。试验梁混凝土顶底板采用SOLID45 三维实体单元,波形钢腹板厚度较薄则采用SHELL181 板壳单元,梁体普通配筋采用LINK8单元。

考虑到嵌入式抗剪连接件通过焊接相连,刚度大、变形小,顶底板与腹板之间的相对滑移可忽略不计,通过结点耦合近似模拟两者之间抗剪连接键作用。支座处施加相应的面约束模拟橡胶支座,试验梁的有限元模型如图8 所示。

图8 试验梁有限元模型Fig.8 Finite element model of test beam

根据有限元模拟分析,试验梁的开裂荷载约为60kN,因此本文弹性加载阶段施加的荷载最大值为50kN,在试验加载过程中,试验梁底板未有可查裂缝出现。

试验加载为集中加载,为避免加载点截面应力集中的影响,实测值以L/4 截面为准。图9 为试验梁L1 -2、L2 -2 和L2 -3 在跨中双点加载作用下,L/4 截面底板的挠度实测值、有限元值和理论分析值。其中,挠度实测值取所测截面内外侧挠度均值。图9 表明,荷载-位移曲线基本呈线性变化,三条曲线吻合度良好,利用能量变分法求得的理论解析解与试验值、有限元值较为接近,验证了理论计算和有限元模型的正确性。

图9 跨中双点加载试验梁L/4 截面底板挠度值Fig.9 Deflection value of bottom plate of L/4 section of test beam under mid-span double-point loading

表2 为波形钢腹板曲线梁L/4 截面的底板挠度均值,由表可知： ①三片试验梁在跨中双点加载工况下,实测值都大于有限元和理论值,这主要是因为所建立的有限元整体式模型与试验梁有差异,试验梁材料因初始缺陷在加载过程中刚度降低; ②从三片试验梁底板挠度对比可知,腹板厚度对挠度变形影响较大,而横隔板数量对挠度影响可以忽略不计。

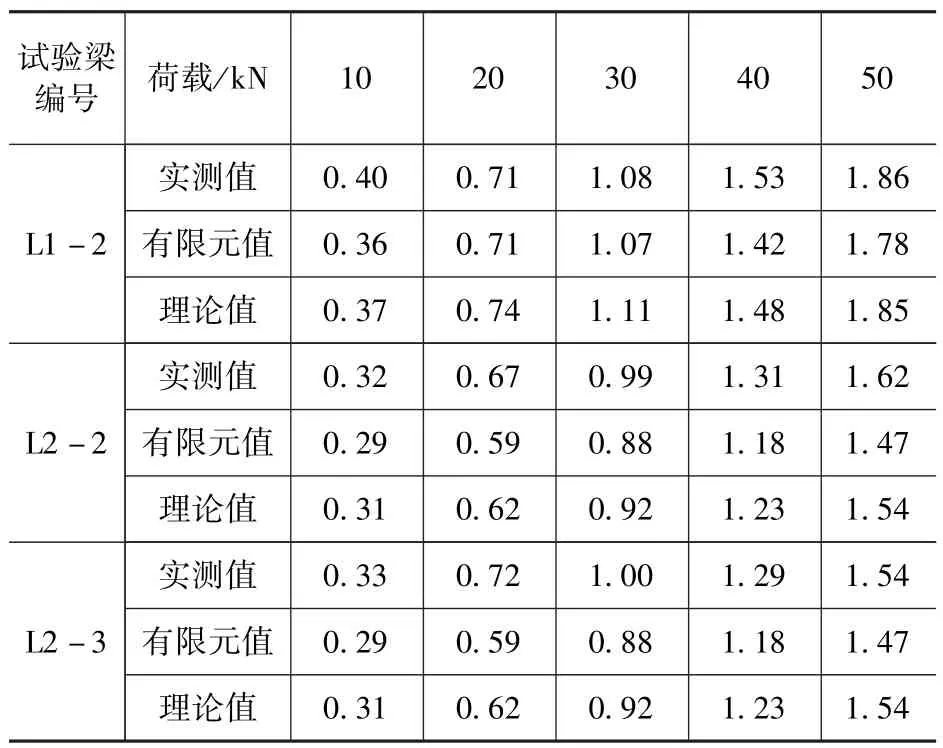
表2 试验梁L/4 截面底板内外侧挠度均值Tab.2 Average deflectionvalue of L/4 section floor of test beam

4 波形钢腹板曲线箱梁挠度偏载系数分析

为研究波形钢腹板组合曲线箱梁的挠度偏载效应,本文以四川绵茂东河3 号桥为计算模型,利用文中箱梁挠度计算理论对其进行相关分析。此桥上部结构为两跨波形钢腹板预应力混凝土箱梁,桥梁跨径布置为80m + 80m,两跨平面分别位于半径为256m 和半径310m 的圆曲线上,本文模型梁仅取其中半径为256m 的一跨,边界条件为简支约束进行偏载分析。

主梁采用单箱单式截面。双车道桥面宽为9m,底板宽为5m,箱梁悬臂翼缘2m,悬臂板端部厚度为20cm,根部厚度为60cm,尺寸详图见图10。箱梁混凝土采用C40 混凝土,波形钢腹板钢材选用Q345C,厚度10mm,波长160cm,波高22cm,水平面板宽43cm,折叠角度为30.7°,见图11。

图10 箱梁截面尺寸(单位： cm)Fig.10 Section size of box beam (unit： cm)

图11 梁横截面及腹板尺寸Fig.11 Size of cross section and web

参照《公路桥涵设计通用规范》中关于公路-I 级车道荷载规定,计算荷载由均布荷载qk=10.5kN/m 和集中荷载Pk=360kN 组成。改变模型几何参数,计算箱梁跨中底板挠度值,研究各参数变化对挠度偏载系数的影响。

对于波形钢腹板曲线箱梁,因曲率半径存在,箱梁的外侧弧长大于内侧弧长,结构重心偏向于曲线外侧,在自重作用下,箱梁外侧挠度大于内侧挠度。文中挠度偏载系数定义为：

4.1 曲率半径对偏载挠度的影响

结合公路和城市立交弯桥的设计需求,保持桥梁跨径L=80m,曲线梁的半径取值为120m ～300m,以20m 幅度为增量单位研究波形钢腹板曲线梁在偏载作用下,曲率半径变化对挠度偏载系数的影响。曲线梁在内、外侧偏心荷载作用下跨中底板挠度偏载系数如图12 所示。

从图12 可以看出： ①在偏载作用下,波形钢腹板曲线箱梁的挠度偏载系数都随着曲率半径的增大而逐渐减小,但挠度偏载系数值皆大于1,说明曲线梁在偏载时外侧底板挠度大于内侧挠度; ②当曲率半径大于200m 以上时,随着曲率半径的增大,外侧偏载产生的挠度偏载系数曲线变化趋于平缓稳定,变化幅值在2%以内,可认为此时波形钢腹板曲线梁扭转变形与直线梁相差无几,可按直线梁进行计算。

4.2 宽跨比B/L 对偏载挠度的影响

为研究箱梁宽跨比对波形钢腹板曲线组合箱梁挠度偏载系数的影响,保持桥梁跨径L=80m不变,箱梁的宽度尺寸依次取为： 8m ～17m,以1m 幅度为增量单位,其余尺寸不变,内外侧偏载作用下产生的挠度偏载系数值如图13 所示。

从图13 可以看出,随着宽跨比的增加,外侧偏载作用下产生的偏载系数逐渐增大,而内侧偏载作用下产生的偏载系数逐渐减小,可认为箱梁宽度对曲线梁外侧扭转变形影响较大。

4.3 高跨比H/L 对偏载挠度的影响

取箱梁的腹板高度为2m ～5m,以0.3m 为增量,保持桥梁跨径L=80m 不变,研究波形钢腹板曲线箱梁在高跨比0.025 ～0.0625 变化时,内外侧偏载产生的偏载系数情况。图14 为采用本文理论求得的计算结果。

图12 曲率半径R-挠度偏载系数ηFig.12 Deflection deflection coefficient of radius of curvature

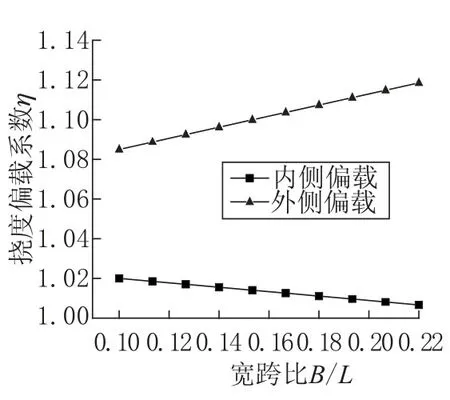
图13 宽跨比B/L-挠度偏载系数ηFig.13 Deflection coefficient of B/L-deflection ratio of width to span

图14 高跨比H/L-挠度偏载系数ηFig.14 Deflection coefficient of B/L-deflection ratio of width to span

从图14 可得： ①在外侧偏载作用下,波形钢腹板曲线箱梁的挠度偏载系数随着高跨比的增大而逐渐增大; ②在内侧偏载作用下,当曲线箱梁的高跨比在0.025 ～0.0625 变化时,挠度偏载系数维持在1.01 附近不变。

5 结论

本文进行了波形钢腹板组合曲线箱梁的偏心内外侧加载试验,建立了模型梁的整体式有限元模型,对其受力过程进行了线弹性分析,试验值与计算值较为吻合,验证了本文计算方法与有限元模型的正确性,并得出以下结论：

1.在集中荷载作用下,波形钢腹板曲线箱梁竖向挠度与腹板厚度有关,与横隔板数量无关。

2.波形钢腹板曲线箱梁的挠度偏载系数都随着曲率半径的增大而逐渐减小,曲线梁的外侧底板挠度大于内侧挠度。

3.曲率半径大于200m 以上时,外侧偏载产生的挠度偏载系数曲线变化趋于平缓稳定,变化幅值在2%以内,可按直线梁进行计算。

4.在外侧偏载作用下,波形钢腹板曲线梁的挠度偏载系数与箱梁的宽跨比、高跨比呈正相关。