B电商智能物流中心订单分波（处理）优化设计

2019-07-12陈增坤余蕾王旭

中国储运 2019年7期

文/陈增坤余蕾王旭

1.1问题的提出

1.1.1 问题背景

B电商智能物流中心24小时不间断接收客户订单，并且所有订单都要求次日达，为了提高多品种、小批量商品的分拣效率和效益，就要首先对商品订单进行分类处理。同时B电商物流中心采用“货到人”的自动化拣选系统，即通过智能搬运机器人实现“无人化”搬运作业模式，在方便快捷的同时也带来了前所未有的挑战，即要合理调度AGV才能以最低成本实现最大效益，而调度的原则便是基于客户的订单信息。因此，智能物流中心的订单处理是提高拣选效率，降低运营成本，实现规模效益的关键环节。

1.1.2 问题分析

在B智能物流中心“货到人”的作业模式下当已知目前的订单情况，则其在仓库中的货位仓储信息已知，因此只需要调度AGV小车将订单品项所在货架全部搬运到拣选台即可完成所有的搬运任务。在物流中心目前的运营中按照客户下单订单的先后顺序划分订单波次，发现这种分波模式下，经常造成AGV小车重复搬运货架，并且由于不同订单分布的移动货架距离较远，使得AGV小车搬运时间较长，且造成运力浪费。为解决上述问题，需要改变当前的订单处理模式，需要基于订单相似性来划分订单波次，即订单品项所在统一个货架的订单分为一个波次，从而可以减少AGV小车搬运次数，提高拣选效率，降低运营成本。

2.1基于总搬运次数优化的订单分波模型

2.1.1 订单分波目标函数

对订单进行分波是为了提高拣选的效率，更有效地完成拣选作业，为了达到这个目的，通常将订单分波的目标设置为总的拣选距离最短或者总的拣选时间最短，这两个目标都为定量并且是容易实现的。在运行的过程中，拣选时间除了与拣选的距离有关外，搬运行走的速度，寻找储位的时间以及设备的自动化程度等因素有关，这些因素往往与整个系统的硬件以及人员设备有关，不受人力的控制，因此通常情况下，订单分波的目标可通过减少总的搬运距离来实现。

以拣选距离最短为目标建立数学模型，首先要为AGV小车设置一定的路径策略，本文采用穿越式策略，这种方式的特点是AGV拣货小车从通道的一段进入，同时从拣选通道两侧寻找分配的货架，抬起后从通道另一端离开，由于行走的路径看上去像是一个“Z”形状，所以又称为“Z”形路径式。

2.1.2 建立模型前的准备

假设AGV拣货小车从货架到拣选台的行驶距离为si，货架i被搬运的次数为ti，AGV拣货小车从货架i到货架i+1之间行驶的距离为di，从起始点到第一个货架行驶的距离为d0，从最后一个货架回到起始点行驶的距离为dn，那么一台AGV拣货小车总的搬运

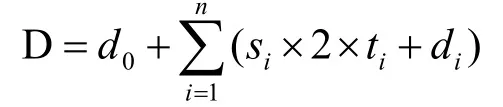
由于AGV搬运小车每次只能搬运一个货架，因此订单在分波前与分波后AGV拣货小车在货架之间的搬运距离和AGV拣货小车从初始位置到第一个货架的距离以及从最后一个货架返回初始位置的行走距离都是必不可少的，这一点也是与“人到货”的拣选方式最大的不同，另外，考虑AGV拣货小车的作业成本，AGV拣货小车在货架之间移动时为空车运行，在货架与拣选台之间为承载货架运行，其成本较高，因此认为AGV拣货小车在货架与拣选台之间的搬运距离重要性更高，影响更大。

对AGV拣货小车的搬运路径进行分析，综合考虑以上因素，认为AGV拣货小车总的搬运距离可以简化为以下公式：

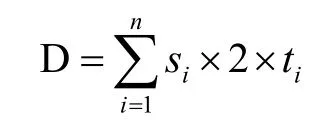
在不考虑AGV拣货小车在哪一个拣选台处拣选的情况下，即假设AGC拣货小车到各个拣选台的搬运距离相同，由于货架与拣选台的位置固定，那么AGV拣货小车搬运货架到拣选台的距离则为固定，因此AGV拣货小车的搬运距离只与AGV拣货小车搬运货架的次数有关，当AGV拣货小车搬运货架的总次数最少时，AGV拣货小车的搬运距离也达到最小。

根据以上分析，同时系统中存在多台AGV拣货小车，假设所有小车搬运的总货架数为N，则本文在对订单分波的过程中，以所有AGV拣货小车搬运货架的总次数最少为目标函数建立数学模型，即目标函数为：

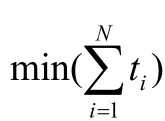
以AGV拣货小车的搬运次数最少为目标函数建立数学模型，可以为订单分波作指导，使得分波有所依据。另外以此目标建立的模型一方面不需要事先确定AGV拣货小车搬运的路径策略，同时在对模型的求解时，大大减少了计算量，方便了问题的求解。

2.1.3 订单分波模型设定

为了建模的方便，本文对系统做了如下假设：

（1）一个订单包含的品项数至少为1。

（2）一个订单只能被分在一个波次中，不允许分割。

（3）一个货架在同一个波次中只能被搬运一次。

（4）不存在缺货的情况。

（5）订单信息已知，并且订单品项在货架中的储位已知。

（6）AGV小车的搬运路线策略已知。

同时在模型的建立中，设置了如下参数，对其进行了定义。

表1 订单分波模型所用参数符号及含义

2.1.4 订单分波模型的建立

根据以上的模型假设及其参数设置，可以将本文研究系统的订单分波问题描述为：假设有M个订单需要拣选，共包含W个品项，所有的品项共分布在N个货架上。现在对这M个订单进行分波，最终使得AGV拣货小车搬运货架的总次数最少。因此，本文中所研究系统的订单分波问题的数学模型如下：

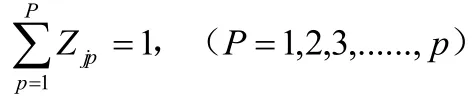
其中为目标函数，表示所有货架被搬运到次数之和最小。通过每一个波次中每个货架的搬运次数，即可求得总的搬运次数。约束条件公式表示每个订单只能被分配到一个波次；公式表示一个货架在一个波次中只能被搬运1次或者0次；表示一个波次的订单总数不能超过周转货架总的储位数D·C。

3.1基于节约算法的订单分波模型求解

订单分波问题属于NP～hard问题，而且其随着订单数量的增多，其计算量呈指数增长，因此对其求精确解相当困难，在研究中通常选择启发式算法对其进行求解。目前对订单分波问题求解的启发式算法有多种，可以归结为种子算法和节约算法两类。本文应用节约算法来对该系统的订单分波进行求解，找出优化的分波结果。

节约算法的提出是为了解决运输问题，在配送的过程中，通常需要完成多个客户的配送作业，根据客户的地理位置以及客户和客户之间的距离，通过将两个或两个以上的客户合并为一起同时配送，来计算节约的运输里程，从而找出节约里程最多的客户合并方式。本文将节约算法应用在配送中心内部AGV拣货小车的搬运过程，通过计算AGV拣货小车节约的搬运货架总次数来对订单进行分波。

3.2节约算法设计

本文应用C++语言对算法进行编译求解，节约算法在求解以上订单分波问题时的计算步骤如下：

（1）在系统中输入当前所有的订单信息，以及周转货架的储位数。每一个订单存放在一个储位上，周转货架的储位数则代表可以存放的订单数。

（2）将所有的订单两两组对，计算其组对后的搬运次数的节约量。假设订单1分布在3个货架上，订单2分布在5个货架上，其中订单1和订单2分布的货架有两个为重复。若按订单别来拣选，那么订单1需要搬运3次，搬运订单2需要5次；而将订单1和订单2划分为一波后，其重复的货架只需搬运一次即可，那么两个订单总的搬运次数变为6次，则订单分波后节约的搬运次数就为2次。

（3）将所有的节约次数按由大到小降序排列。

（4）选择节约次数最大的两个订单组合作为初始订单波量。

（5）首先以这两个初始订单组合为基准，找出与这两个订单同时位于同一货架上的订单，加入到该波次中来：其次再分别以这两个订单为基准，比较其与其他订单的节约量，按节约量由大到小的顺序降序排列，选择节约量最大的订单划入该波次。

（6）重复步骤（5），直到该波次的订单数不满足周转货架所包含的储位数，那么已完成该波次的分波作业。

（7）不断的重复步骤（4）～（6），直到所有的订单都完成分波。

在本文的研究中，通过C++语言对算法进行实现。在实际的应用中，将配送中心收到的顾客订单进行处理，获取订单的货架信息，将订单及其货架信息输入算法中来，通过运行最终将返回订单的分波结果。由于在实际的电商配送中心中，订单量巨大，为了对所用的算法做出更加清晰地解释，故对实际的配送中心进行了一定的假设并随机产生少量的订单来证明算法的有效性。

4.1订单分波模型效果分析

B电商智能物流中心的分拣作业均在拣选站台完成，拣选站台按照波次订单进行拣选作业，由于不同订单调度AGV小车搬运的移动货架不同，而不同移动货架到各个拣选台的位置不同，因此将客户订单依据AGV小车总搬运距离最短的原则划分波次，将同一波次订单分配到同一个拣选站台，可以有效减少重复搬运、均衡搬运作业，缩短搬运时间，从而降低智能搬运机器人能量损耗、提高拣选作业效率。