基于DQN的企业创业创新自主体模拟

李 睿,王 铮,2

(1.华东师范大学地理信息科学教育部重点实验室，上海200241；2.中国科学院科技政策与管理科学研究所，北京100080)

0 引言

基于自主体的模拟是一种非常流行的模拟方法，在许多学科中得到了广泛的应用。能够使用该方法进行模拟的事物存在3个主要原则[1]：

1)存在大量能够相互作用或者与环境作用的客体；

2)客体是自主运行的，不允许对其行为进行中央或“自上而下”的控制；

3)能够对客体相互作用的结果进行数值计算。

Tesfatsion(2001)认为现代经济系统是一个复杂自适应系统，它由分散的、在不同市场环境中相互作用的自主体集合组成，并且具有自主创新能力[2]。这表明现代经济系统存在使用自主体模拟的理论基础，因此本文采用经济学领域的自主体模拟方法——ACE(Agent-based Computational Economics)方法，对以企业为基础经济系统进行了演化的实验模拟。

Wang，Dai(2010)基于自主体的建模，将知识产权保护制度作为考察企业对不同环境反应的制度因素，研究了研发政策对高科技创业企业发展的影响[3]；顾高翔，王铮，姚梓璇(2013)将中国划分为362个有创新能力的资本组织，通过比较不同的金融政策，对经济危机发生的原因和解决经济危机的办法进行了探究[4]；Bures(2014)在NetLogo平台上构建了一个包含消费者自主体，工厂自主体，采矿自主体和运输自主体的经济系统，通过研究该系统随时间的变化规律探究ACE的有效性和合理性[5]；Monett(2016)同样在NetLogo平台上构建了一个包含存款者自主体，借款者自主体，银行自主体的经济系统，并通过设置不同的参数研究不同情景下银行破产的可能性[6]；Kouwenberg(2015)建立了美国住房市场的自主体模型，发现该模型比标准模型能够更好地预测美国住房市场的价格变化[7]；Chen(2017)以鄱阳湖生态经济区为研究对象，构建了一个生态产业链的自主体模型，该模型不仅讨论了企业与政府之间的博弈关系，而且分析了产业链中企业之间利益关系的演化规律[8]；Tang(2015)建立自主体模型研究不同CET(Carbon Emissions Trading)计划的影响，从而找到最适合中国的CET计划，实验结论认为该模型是一种有效的政策制定和分析工具[9]。但是在上文提及的研究中，自主体都不具有实时的智能性，只能通过事先定义的数学表达式表达偏好和产生行为，对环境变化反应的自适应能力不足。这对于一个复杂的经济系统来说，自主体个体判断往往会出现偏差。

随着信息化社会的发展，越来越多的高新技术产业在推动社会经济的发展中起到了至关重要的作用。产业的发展模式，技术的进步速度，规模的扩张程度和高新技术的研发方式都成为了需要关注的问题。本文根据这些特点，构建了一个由高新技术企业驱动的经济系统，并采用ACE方法分析企业行为和技术发展，研究其在不同企业和经济形势下的变化路径。

本文的经济系统模型主要参考了Zhang(2003)[10]，戴霄晔(2007)[11]和Wang，Dai(2010)[3]的工作。在他们的工作中，企业在模拟过程中无法动态分配其研发投入的比例。戴霄晔(2007)[11]和Wang，Dai(2010)[3]使用回归分析的方法，得到了最优创新投入比，但依旧是一个固定数值，无法动态变化。因此，本文把研究重心放在了如何使自主体智能地调整研发投入比例之上。

本文采取的人工智能算法DQN是AlphaGo的前身。2016年Deepmind将MCTS(蒙特卡洛树搜索)与DQN结合，开发出了AlphaGo的初代版本。本文认为企业进行正确的决策行为就像是AlphaGo在下一步胜率最高的棋。

1 经济系统模型

本研究将企业个体定义为自主体。为了模拟自主体间相互作用的强弱，将自主体划分为不同的“区域群组”，“区域群组”内自主体的行为模式更多地受到本群组成员的影响，存在着较为紧密的一致性(比如相似的创新研发策略)，而受到其他群组自主体的影响较微弱，不同群组自主体的行为方式也存在差异。在现实世界中，企业的行为模式也会因为区域差异的不同而不同，区域尺度可以是市际，省际甚至国际。企业群便以区域为组织形式存在，区域便对应本研究中的“区域群组”，同区域内的企业互相影响，存在较高的相似性，而不同区域的企业则存在较大的不同。每一期模拟中，对于每一个企业自主体，存在4个阶段：创业行为，生产行为，市场行为和创新行为。

1.1 创业行为

设每个企业自主体在模拟的开始阶段，如果处于未创业状态，则该企业在第t期的创业概率为：

(1)

式(1)中，Pri,j,t是第i组第j个企业在第t期的创业概率，Ki,j,t是第i组第j个企业在第t期的资本存量，ai,j,t是第i组第j个企业在第t期的企业存在年限，P0是初始基本创业概率。公式(1)认为，企业的创业行为会受到组内其他企业之前创业结果的影响。当组内有较多的企业发展较好(企业存在时平均每年的资本较高)，在这种情况下，其他企业(自主体)则更乐意去创业，创业概率较大。

1.2 生产行为

若一个企业已经创业成功，则会开始筹集资本投入生产，本经济系统的生产函数以Cobb-Douglas函数形式定义：

Yi,j,t=hi,j,tKi,j,tα(α<1)

(2)

式(2)中，Yi,j,t是第i组第j个企业在第t期制造的产品量，hi,j,t是第i组第j个企业在第t期的生产技术水平，Ki,j,t是第i组第j个企业在第t期的资本存量，α是资本弹性指数。

企业在制造产品之后，将产品投入市场，各企业制造的产品之和是市场总体供给，产品的市场价格由市场供需和市场供给共同决定，将企业在这一过程中获得的利润定义为：

πi,j,t=PtYi,j,t-cYi,j,t

(3)

式(3)中，πi,j,t是第i组第j个企业在第t期的利润，Pt是第t期的产品市场价格，Yi,j,t是第i组第j个企业在第t期制造的产品量，c是产品成本系数。

1.3 市场行为

企业在创业成功后，开始制造产品，而每一期的市场供需现状决定了该期的产品价格。第t期的产品价格定义为：

(4)

式(4)中，Pt是第t期的产品价格，Dt是第t期的市场需求，St是第t期的市场供给。

市场供给St定义为第t期市场中每个企业制造的产品Yi,j,t的总和：

(5)

市场需求Dt定义为：

Dt+1=Dt*(1+gt+bt+εt)

(6)

式(6)中，gt是衰减函数，bt是周期函数，εt是随机扰动项，共同反映了随着时间的进行，市场需求的增长率在生产周期内逐渐衰减的规律：

(7)

(8)

εt∈U(-0.02,0.02)

(9)

1.4 创新行为

企业创业后，就会研发，导致创新。这里的经济系统定义了两种创新行为：自主创新和模仿创新。研发行为的规则定义为：

当πi,j,t>0时，

INi,j,t+1=INi,j,t+m*n*πi,j,t

(10)

IMi,j,t+1=IMi,j,t+(1-m)*n*πi,j,t

(11)

Ki,j,t+1=(1-d)Ki,j,t+(1-n)πi,j,t

(12)

当πi,j,t≤0时，

Ki,j,t+1=(1-d)Ki,j,t+πi,j,t

(13)

其中，INi,j,t是第i组第j个企业在第t期投入自主创新研发的资本，IMi,j,t是第i组第j个企业在第t期投入模仿创新研发的资本，n是本期投入创新研发的总资本占本期获得利润的比例，m是本期投入自主创新研发的资本占本期投入创新研发的总资本的比例，d是资本折旧系数。

创新研发资本的不停投入，最终量变引起质变，获得技术进步，这一过程的规则定义为：

当INi,j,t≥f(Ki,j,t)时，

(14)

(15)

INi,j,t+1=INi,j,t-f(Ki,j,t)

(16)

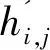
当IMi,j,t≥g(Ki,j,t)时，

(17)

IMi,j,t+1=IMi,j,t-g(Ki,j,t)

(18)

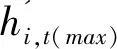
创新研发获得技术进步的阈值准则取作：

f(K)=βK3

(19)

g(K)=μK3

(20)

其中，β是自主创新研发的难度系数，μ是模仿创新研发的难度系数。

另外，当企业的资本存量过小时，企业将破产，资本归零，保留当前技术水平，在后期的模拟中仍有机会重新创业。

此处，将定义一个特殊的企业自主体，该企业在每期模拟中的基本研发行为模式遵从上文的模型，但是该企业能够根据下文的人工智能算法DQN评估在每期模拟中如何分配获得的利润，对企业自主创新研发比例m和企业投入研发比例n进行自适应调整。一共有9种可能的政策行为情景：

1)企业自主创新研发比例m和企业投入研发比例n不变；

2)提高企业自主创新研发比例m和企业投入研发比例n；

3)提高企业自主创新研发比例m，企业投入研发比例n不变；

4)企业自主创新研发比例m不变，提高企业投入研发比例n；

5)降低企业自主创新研发比例m和企业投入研发比例n；

6)降低企业自主创新研发比例m，企业投入研发比例n不变；

7)企业自主创新研发比例m不变，降低企业投入研发比例n；

8)提高企业自主创新研发比例m，降低企业投入研发比例n；

9)降低企业自主创新研发比例m，提高企业投入研发比例n。

其中，由于现实中企业创新研发策略存在延续性，不可能在短时间内大幅度改变，因此将提高和降低m，n的规则定义为：

mt+1=mt+(1-mt)*0.1

(21)

mt+1=mt*0.9

(22)

nt+1=nt+(1-nt)*0.1

(23)

nt+1=nt*0.9

(24)

其中，式(21)和(23)是提高m、n的规则，提高的幅度分别是模拟创新研发比例(1-m)和企业投入再生产比例(1-n)的10%；公式(22)和(24)是降低m、n的规则，降低的幅度分别是自主创新研发比例m和企业投入研发比例n的10%。

该企业可以通过以上9种方式调整m和n，满足自身偏好的同时适应环境，而如何进行有效且智能的调整是本文的重点研究内容。

2 作为自适应学习行为的DQN算法模型

自主体的一个特点是自适应学习。调整自主体或者说指导自主体从环境中学习知识的算法，称之为强化学习(Reinforcement Learning)。自主体的自适应学习需要强化学习的帮助，DQN(Deep Q-Network)算法就是这么一种强化学习算法，它最为经典的前身，是Watkins提出的Q学习(Q-learning)算法[12]。算法伪代码如表1所示。

表1 Q学习算法伪代码Tab.1 Pseudo code for Q-learning

在程序段1中，首先定义一个函数Q(s,a)，该函数能够根据当前状态s评估自主体各种可能的行为a。然后在环境探索过程中，自主体会选择一个行为at，at有ε的概率选择随机行为，否则就是选择使Q(s,a)取值最大的行为at。此时，自主体执行at并转移到下一状态st+1，同时得到回报r，最后根据公式Q(st,at)=Q(st,at)+α[r+γmaxaQ(st+1,a)-Q(st,at)]更新Q(s,a)。可见，Q学习算法主要是通过自主体大量地探索环境，获得能够指导自身行为的Q(s,a)，从而适应环境。但是在Q学习算法中，状态和行为空间离散且维数不高，此时可使用Q(s,a)储存每个状态行为对(s,a)的Q值，而当状态和行为空间高维连续时，Q(s,a)的存储是一个难题。当前最通用的做法是把Q(s,a)的更新问题变成一个函数拟合问题，相近的状态得到相近的输出行为。

2013年，人工智能研究团队DeepMind提出了DQN(Deep Q-Network)算法，将深度学习和强化学习结合起来训练自主体，利用深度神经网络的泛化能力存储Q(s,a)，使得自主体可以直接根据屏幕像素点输出游戏动作。该算法在Atari 2600游戏中取得了惊人的效果：在参与实验的7个Atari 2600游戏中，自主体有6个游戏超越了之前所有的强化学习方法，并且有3个游戏超过了专家级别的人类玩家[13]。本文会将企业自主体的各项状态值以及市场条件等作为DQN的观察值输入，输出得到当前市场环境下最符合企业偏好的决策行为，同时进行强化学习。通过这种学习，企业自主体会在经济实际运行中评估自己的行为，例如它对创新的效应行为。2013版本DQN算法的伪代码如表2所示，这个算法模型，刻画了企业自主体的自适应创新行为。

表2 2013版本DQN算法伪代码Tab.2 DQN pseudo code (ver. 2013)

2015年，DeepMind更进一步，在DQN的基础上提出了带有目标Q函数的DQN，提升了自主体适应环境的速度和准确度[14]。

在2015版本DQN的基础上进行改进的方法主要有Hasselt等提出的Double DQN[15]，Schaul等提出的Prioritized Replay[16]和Wang等提出的Dueling Network[17]。本文采用了Double DQN，该算法训练两个Q网络，一个负责选择行为，另一个负责评估行为，随后两个Q网络交替进行更新，可以部分消除Q学习中经常出现的过优化[18]。

本文使用Python实现上述经济系统模型及DQN。主函数的代码如表3所示。

首先，初始化经济系统模型作为自主体运行环境env，再初始化作为自适应学习行为的DQN模型agent。随后进入两个循环，第1个循环是模拟次数EPISODE，第2个循环是每次模拟的模拟期数STEP。在每次模拟开始时，都要根据经济环境对自主体可观察的状态state进行初始化，该状态包含了表3中的12个观察指标。在模拟周期中，自主体首先根据自身状态得到其认为最优的行为action，随后自主体执行该行为，环境也随之发生变化，同时返回自主体下一期可观察的状态next_state，回报函数值reward，以及判断模拟周期是否结束(期数到200期或者企业自主体破产)的逻辑值done。DQN模型就根据自主体本期可观察的状态state，行为action，回报函数值reward，下一期可观察的状态next_state，判断模拟周期结束与否的逻辑值done，以及当前模拟次数episode进行自适应学习。最后，将本期可观察的状态state赋值为下一期可观察的状态next_state，并判断当前模拟周期是否结束，若不结束，继续进行下一期的模拟，若结束，则重新开始一次新的模拟周期。

表3 Python主函数代码Tab.3 The Python main function code

3 模拟结果与分析

3.1 参数确定

首先，在经济系统模型中存在着大量的外生参数，类似的，在DQN中存在着大量的超参数(超参数是开始机器学习过程之前设置值的参数)，这些参数的初始设置对于模型的正常运行有着重要的作用。经济系统模型和DQN的参数初始值设定见表4和表5。表4的经济系统模型参数还是主要参考了Zhang等[10]和戴霄晔等[11]的工作，表5的DQN超参数则是根据深度强化学习原则调整得到的运行结果较好的参数。

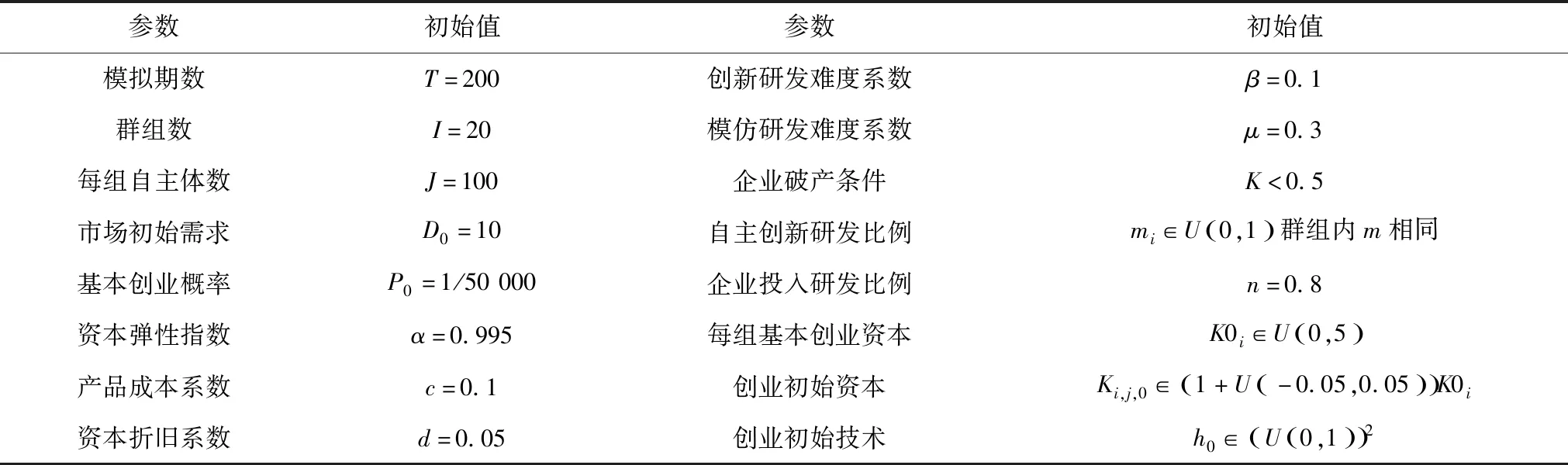
表4 经济系统模型参数确定Tab.4 Parameter determination of economic system model

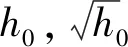
表5 DQN超参数确定Tab.5 Determination of DQN hyper parameter

根据表5，本文的DQN模型构建了2个6层的神经网络，每层拥有神经元60个。神经网络学习率为0.9，回放样本库大小为50 000，并且每次从中随机选择2 000个样本进行训练。企业自主体的初始随机选择率为0.5，随着训练的进行，逐渐下降到0.1。DQN一共进行4 000次模拟，每次模拟的模拟期数均为200期，以此探索和熟悉经济系统的环境。另外，神经网络层与层之间激活函数的选择能够显著地影响信息在层之间的传递，从而影响训练优化的效率，需要慎重选择，常见的激活函数有Sigmoid，Tanh等。本文选择ReLU(Rectified Linear Unit)激活函数，该激活函数的优点在于避免了神经网络训练过程中容易出现的梯度爆炸和梯度消失问题，活跃状态的稀疏性更符合仿生学原理[19]。ReLU激活函数的数学表达式为：

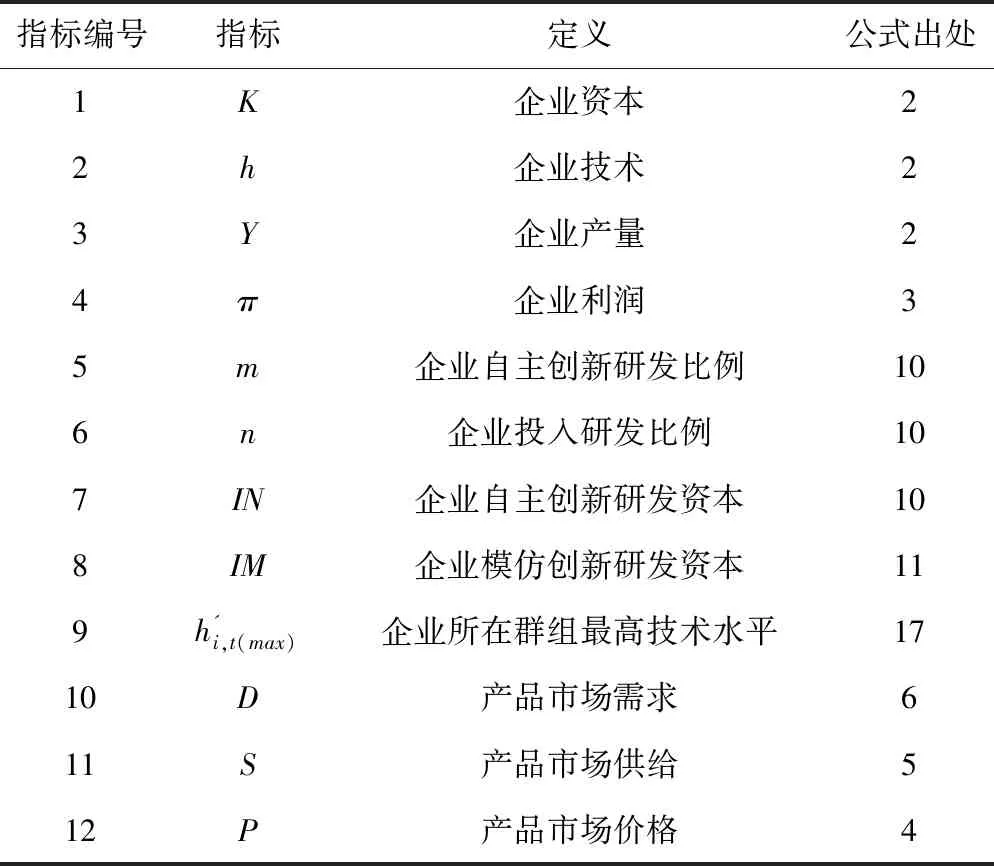
表6 企业自主体观察指标Tab.6 The observation indicators of enterprise agent

f(x)=max(0,x)

(25)

另外，在每期模拟中，企业自主体通过12个能够被自己观察到的指标对环境进行了解(与之相反的，诸如其他企业自主体的资本，技术等指标属于商业机密，是无法被观察到的)，指标的定义及公式出处见表6。

根据表6，企业自主体通过观察自己的内部信息(指标1-8)，群组信息(指标9)，以及整个经济系统的信息(指标10-12)，对调整自主创新研发比例和投入研发比例的行为进行自适应学习。

3.2 回报函数设置和企业自主体的个性

对于一个企业而言，决定它未来行为的不仅仅是当前环境和企业自身的状态，还有企业的个性。企业的个性与回报函数的设置有关，本文定义了三种企业个性，分别是：重视资本和利润，重视技术水平以及重视三者。设置不同企业个性的意义在于，通过观察不同个性的企业对环境反应的不同，能够对不同企业偏好对企业决策的具体影响进行研究分析。而不同的企业个性可以通过模型表达，对应的回报函数分别为：

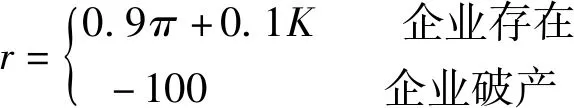
(26)

(27)

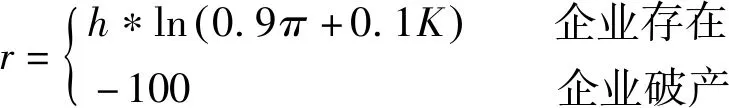
(28)

其中，一旦企业破产，回报都会设置为-100，这是对企业的一个极大的惩罚回报，因此企业会尽可能地避开极具破产风险的行为，从而在剩下的行为中选择符合自身性格特点且回报最大化的行为。

3.3 模拟结果

定义参与行为训练的特殊企业为“实验企业”。将实验企业的创业初始技术水平设置为平均值0.25(所有企业的创业初始技术水平满足分布h0∈(U(0,1))2)，创业初始资本设置为组平均值K0i(群组内企业的创业初始资本满足分布Ki,j,0∈(1+U(-0.05,0.05))K0i)。可以看到，这是一个初始条件很普通的企业，并且模拟过程中实验企业一旦破产，不可重新创业。

为了保证模拟结果的稳定性，一共进行了1000次模拟，并对每期模拟中实验企业的资本，技术，产量和利润在组内的排名进行记录，取平均值，以此衡量该企业对本经济系统环境的适应程度，其中为了使平均值能够反映出破产带来的不良影响，实验企业一旦破产，本期的各项排名就定义为100，可见，组内平均排名是实验企业的模拟表现和破产表现的共同反映。

3.3.1 普通实验企业

首先，将没有使用DQN进行自适应学习的实验企业定义为“普通实验企业”(即企业自主创新研发比例m和企业投入研发比例n始终不变)。普通实验企业的表现见图1，其中横轴为模拟期数，纵轴为组内排名。

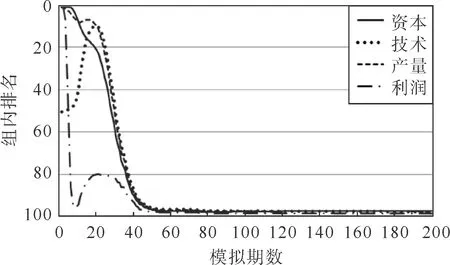
图1 普通实验企业各项指标组内排名变化Fig.1 The change of indicators’ rank of common experimental enterprise in its group

可以看到，普通实验企业在前10期模拟中的盈利表现不佳，由于这一阶段环境中大量的企业开始创业，产量大幅增加，使得产品的市场价格迅速下降，而普通实验企业又缺乏有效的调整措施，因此这一阶段普通实验企业的利润经常处于负值状态，故排名甚至比处于未创业状态的企业还低(未创业的企业该期利润为0)。在第10期至第20期之间，普通实验企业对创新研发的投入收到了成效，技术水平进步很快，并带动了利润的提升。但是在第20期至第40期之间，由于存在模仿创新机制，其他企业能够快速地提升自身技术水平，普通实验企业的技术优势不复存在，并且普通实验企业的初始技术水平并不是顶尖的，在此期间存在着部分技术水平高过普通实验企业的新创业企业。随着技术水平的逐渐落后，普通实验企业的资本与产量排名也渐渐落后，并且在第40期左右，普通实验企业破产的次数大增，所以四项指标的排名均靠后。只有在极少量的模拟中，普通实验企业可以坚持到第50期之后仍然没有破产。

可见，普通实验企业由于缺乏调整措施，并且不存在初始资本与技术优势，所以在模拟初期的破产风险极高，这与现实中能够通过调整自身创新研发投入策略的真实企业相差甚远。

接下来，本文将训练完成的DQN自适应实验企业进行行为决策，由于企业个性的不同，最终企业的行为模式也大不相同。

3.3.2 重视资本和利润的实验企业

重视资本和利润的实验企业根据公式(26)的回报值进行自适应学习，其各项指标排名表现见图2，其中横轴为模拟期数，纵轴为组内排名。研发投入比例的变化见图3，其中横轴为模拟期数，纵轴为比例值。

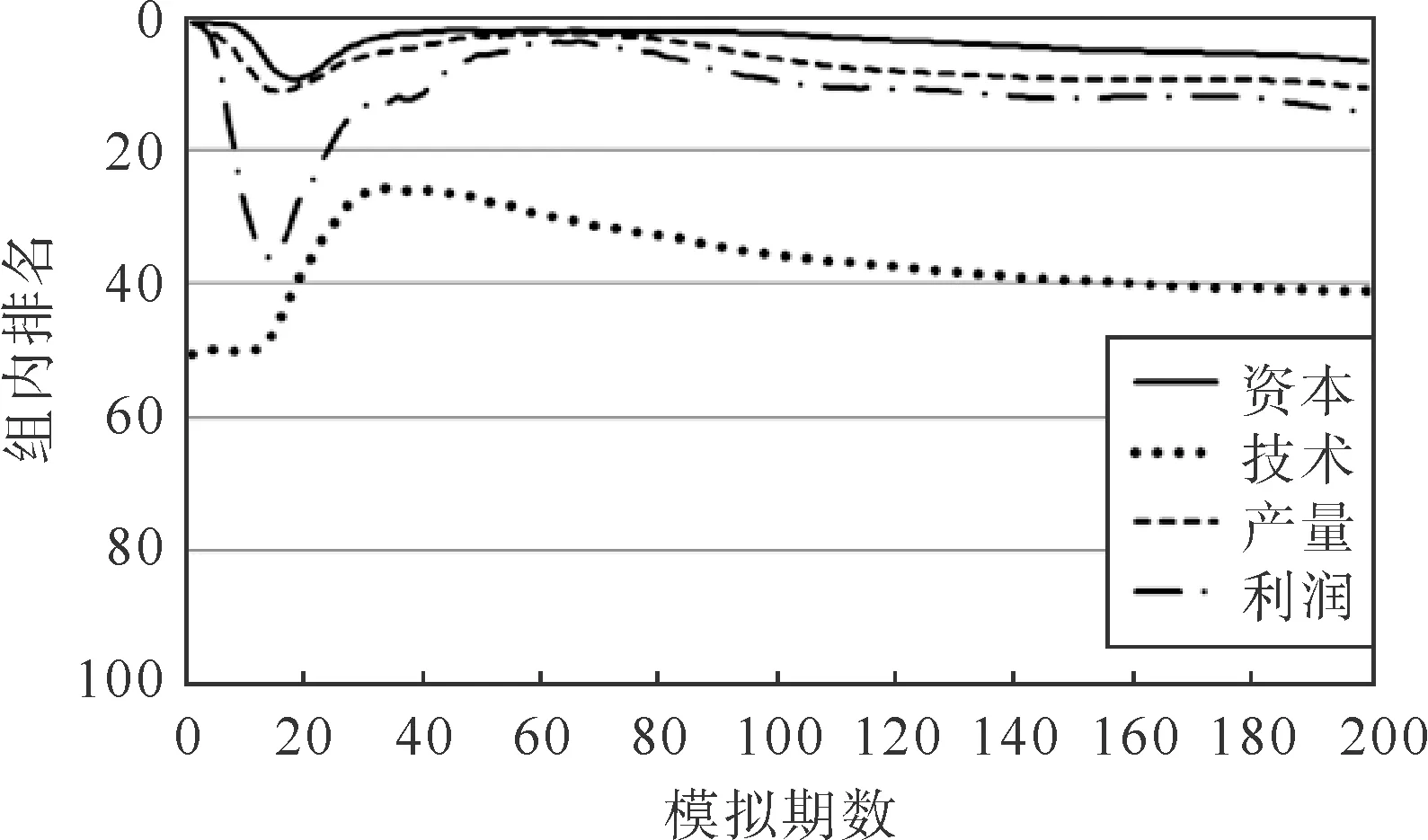
图2 重视资本和利润的实验企业各项指标组内排名变化Fig.2 The change of indicators’ rank of experimental enterprise that values capital and profit in its group

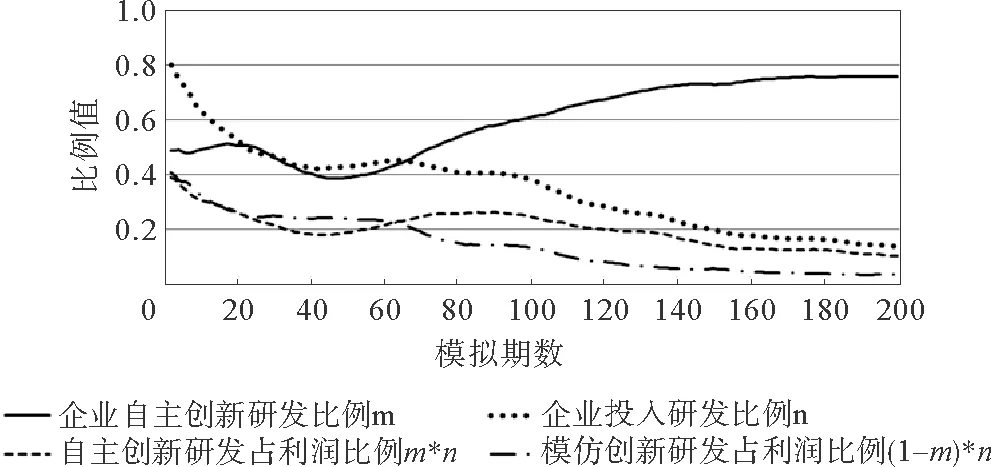
图3 重视资本和利润的实验企业研发投入比例变化Fig.3 The change of the proportion of R&D investment of experimental enterprise that values capital and profit in its group

可以看到，变化曲线存在和普通实验企业相似的地方，即在前20期模拟中，随着产品市场价格的下降，实验企业的利润排名不可避免地下降，但是实验企业迅速地调整了企业投入研发比例，将更多的利润投入扩大再生产中，从而提高了产量，实验企业得以迅速摆脱破产危机，代价便是这段时期实验企业的技术水平进步有限。在第20期与第60期之间，实验企业进入了一个发展的黄金期，尤其是资本，产量和利润排名迅速升至组前列，技术水平也随着研发投入的累积得以进步。在第60期之后，由于实验企业资本的巨大体量，技术上的进步与组内其他企业相比较慢，并且模拟中的这一时期存在一定的破产现象，平均排名逐渐下降，再加上该企业更加重视当前的资本和利润，故实验企业选择继续降低企业投入研发比例，但是选择增加企业自主创新研发比例，因为自主创新研发的资本消耗比模仿创新研发的少，更容易推动技术进步。

3.3.3 重视技术水平的实验企业

重视技术水平的实验企业根据公式(27)的回报值进行自适应学习，其各项指标排名表现见图4，其中横轴为模拟期数，纵轴为组内排名。研发投入比例的变化见图5，其中横轴为模拟期数，纵轴为比例值。

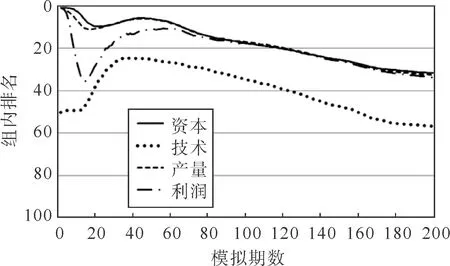
图4 重视技术水平的实验企业各项指标组内排名变化Fig.4 The change of indicators’ rank of experimental enterprise that values technology in its group

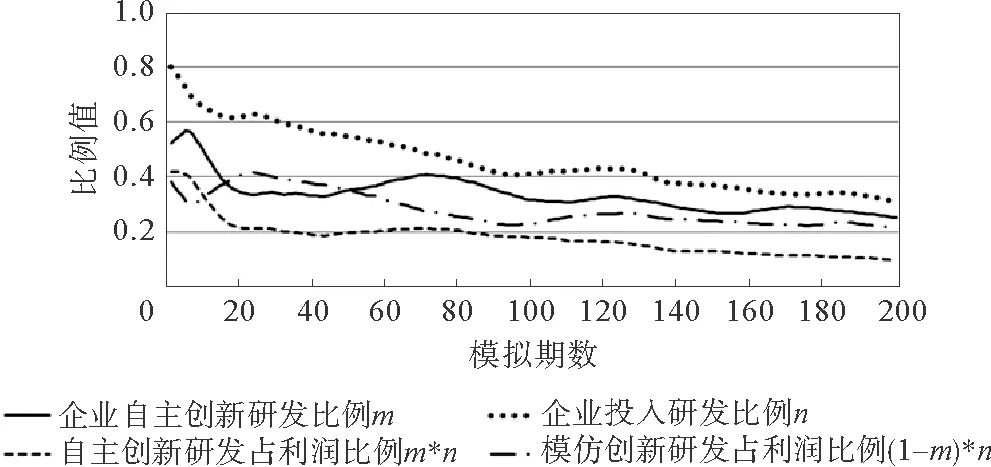
图5 重视技术水平的实验企业研发投入比例变化Fig.5 The change of the proportion of R&D investment of experimental enterprise that values technology in its group

该实验企业在模拟前60期的表现与重视资本和利润的实验企业极为相似，但是在第60期之后，实验企业的表现不佳，破产出现的次数大增，因此各项指标排名快速下降，可以看到造成这一区别的是：虽然面临着后期大增的破产风险，重视技术水平的实验企业没有快速调整企业投入研发比例，而是逐步调低且始终保持在0.3以上，并且与重视资本和利润的实验企业相比，重视技术水平的实验企业把更多的利润投入到模仿创新研发中，因为一旦模仿创新研发成功，对技术水平的提升是巨大的，这符合实验企业的回报函数激励。总体上看，由于通过投资创新研发引导技术进步这一过程存在滞后性，并且回报函数并没有重视资本存量，所以该企业对破产风险的控制不够好。

3.3.4 重视三者的实验企业

重视三者的实验企业根据公式(28)的回报值进行自适应学习，其项指标排名表现见图6，其中横轴为模拟期数，纵轴为组内排名。研发投入比例的变化见图7，其中横轴为模拟期数，纵轴为比例值。

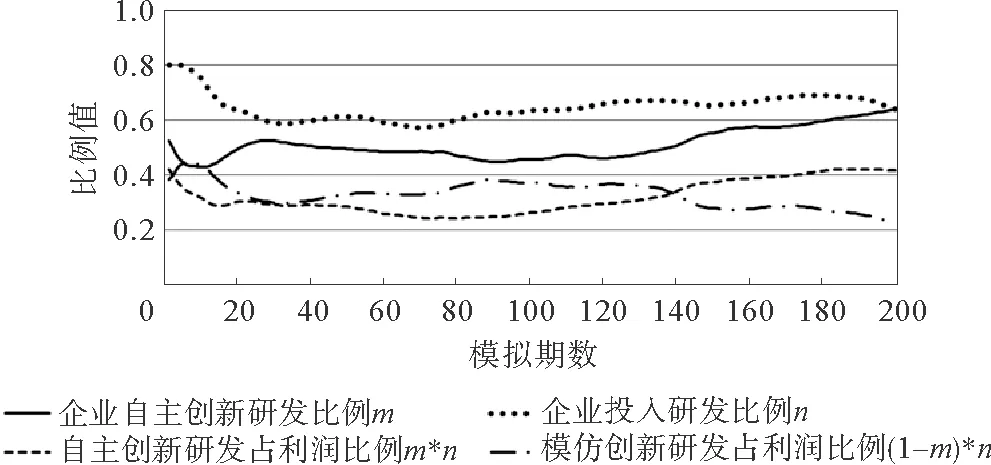
图7 重视三者的实验企业研发投入比例变化Fig.7 The change of the proportion of R&D investment of experimental enterprise that values all of three indicators in its group

虽然重视三者的实验企业资本，产量，利润排名变化和重视技术水平的实验企业类似，但是其技术的平均排名表现更好，第200期仍维持在第40名左右，说明其技术水平更高，且破产出现的次数较少，但依然存在。

实验企业自始至终保持着较高的企业投入研发比例，大部分时间在0.6以上，并且自主创新和模仿创新在不同的时期交替占据主要地位，反应了实验企业不同时期对企业创新的需求。根据较高的企业投入研发比例，可以分析得出该实验企业对资本和利润与技术之间关系的理解，即实验企业认为技术的进步可以促进资本和利润的增长，资本和利润的增长也可以反过来保障技术的进步，这与回报函数的设置相吻合。

3.3.5 数值变化

由于组内排名只能分析该种类型的实验企业相对于组内其他企业的表现情况，无法对比不同类型实验企业表现情况的优劣。因此仍需记录实验企业具体数值的变化，横向分析三种类型实验企业的发展变化。对三种类型实验企业1 000次模拟的各项指标数值变化的平均值进行记录和分析，定义实验企业破产后的指标数值为0。各项指标的数值变化见图8，其中横轴为模拟期数，纵轴为各项指标在模拟中得到的数值。

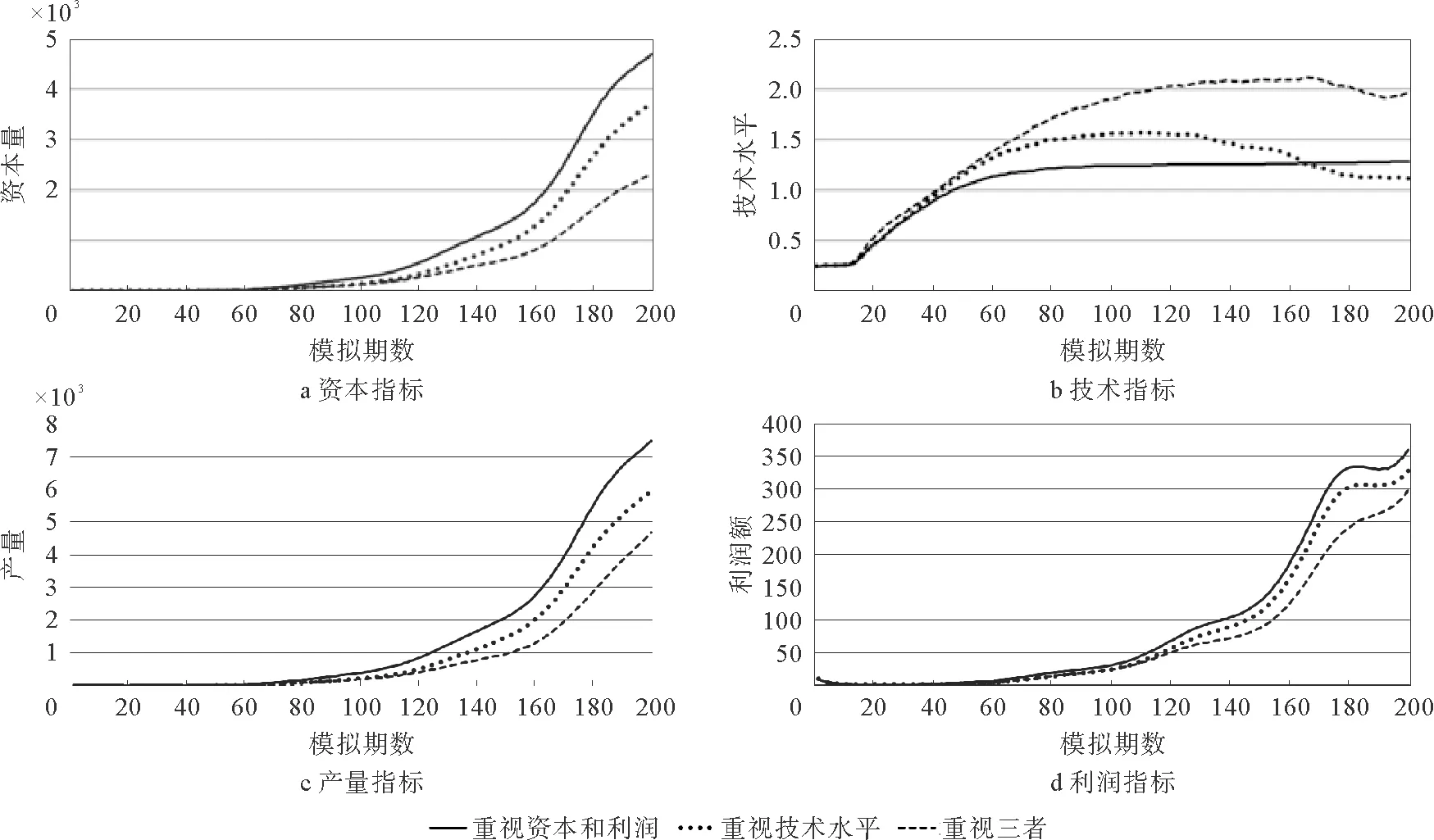
图8 3种类型实验企业各项指标数值变化Fig.8 The change of indicators of three types of experimental enterprise

从图8的a、c、d可以看出，资本，产量，利润这3个指标之间的相关性很强，只要资本增长的速度稳定，产量和利润就可以稳定增长。而资本增长的速度一旦发生变化，如资本曲线在第160期和第180期斜率的变化，对利润的影响较大，利润曲线会出现明显的波动。这3个指标的整体表现：重视资本和利润的实验企业 > 重视技术水平的实验企业>重视三者的实验企业。但是从图8b技术指标的表现看，重视三者的实验企业远远好于另外两种实验企业，重视技术水平的实验企业在中期的表现优于重视资本和利润的实验企业，但是由于其对资本指标的重视程度不够，模拟时后期破产的次数很多，所以其后期的表现不如重视资本和利润的实验企业。

4 讨论与结论

本文利用实验企业自主体模型探索了一个经济系统环境，但是存在着DQN训练时间不足，超参数设置不尽完美等问题(比如，击败柯洁的AlphaGo版本——AlphaGo Master有40层神经网络，使用4块TPU进行了长达数十天的训练，下一场围棋就需要耗费3 000美元电费，可见只有类似Google这种资本与人力条件充沛的公司才能全面引导相应算法的开发项目，但我们依旧可以借助DQN等具备自适应学习能力的算法对经济领域进行探索性研究)，所以仍然存在着一定的破产风险，并拉低了实验企业自主体的组内排名。尽管如此，我们还是可以明显地看出其表现远远胜过普通的实验企业自主体，模拟发现了：企业自主体的确可以通过探索一个企业创业创新经济系统，从而获得一定的智能性，为企业创业创新提供决策依据。

根据实验企业自主体的各种表现，包括指标组内排名和数值变化，可以得出以下结论：

1)无论哪种类型的企业自主体，在创业初期，都必须降低研发投入比例，将更多的资本投入扩大再生产中，这一举措极大地降低了普通企业自主体在创业初期面临的破产风险，但是由于模型缺少博弈机制(类似AlphaGo训练中的自我对弈机制)，企业自主体的大局观还有所欠缺。

2)重视资本和利润的企业自主体的回报函数决定了其决策会在资本和利润与破产风险之间权衡，由于其更多地考虑资本和利润，因此破产风险最小，但是该种企业自主体并没有在技术进步与资本和利润的提升之间建立强烈的联系，模拟期间企业研发投入始终在下调。

3)重视技术水平的企业自主体则是在技术水平与破产风险之间进行权衡，因为对创新研发的投资并不能立刻带来资本的提升，存在滞后性，并且自主创新研发有50%的可能性失败，所以其破产风险较大。

4)重视三者的企业自主体同时考虑到了资本、利润和技术水平，并在技术进步与资本和利润的提升之间建立起一定的联系，对创新研发的投资是最多的，技术水平也是最高的，但是其资本，产量，利润这三个指标的表现不如另外两种企业自主体。