高速列车传动系可靠性的外部影响因素评估

刘玉梅 ，陈 云 ,2，赵聪聪 ，熊明烨 ，乔宁国

（1.吉林大学交通学院，吉林 长春 130022；2.北华大学土木与交通学院，吉林 吉林 132013；3.吉林农业大学工程技术学院，吉林 长春 130118；4.伊利诺伊大学厄巴那-香槟分校自由艺术与科学学院，伊利诺伊 香槟 IL61801）

传动系统是高速列车走行部的关键组成部分[1]，同时承受来自轨道和车体的各种振动和冲击，其可靠性直接影响高速列车的行车安全和使用寿命.高速列车的实际行驶环境非常复杂，传动系主要部件的使用性能必然会受到外部因素不同程度的影响，从而影响传动系的可靠性[2-4].

本文以系统工程理论为基础，从系统工程的视角出发，基于FID （fuzzy influence diagram）对高速列车运行可靠性的外部影响因素进行分类分析.通过对人员、基础设施、环境、维修、管理等外部影响因素的分析，依据FID 理论构建模糊影响图，依据模糊集合理论对各个影响因素进行分析[5]，并确定影响最显著的因素，提出相应的提高传动系可靠性的对应措施.

1 FID 基本理论

模糊影响图结合了模糊集合理论与影响图分析方法来对目标事件进行风险评估[6].模糊集合理论是模糊数学的基础，用隶属度来表示研究对象与对应模糊集合的关系[7].FID 中的模糊集合及表示形式见文献[6].

影响图是一种无环路有向图，由结点和有向弧组成，其图解形式及含义见参考文献[6].结点分为独立结点与非独立结点.按照层次关系将影响图分为函数层、关系层和数值层[8].

在对研究对象进行FID 评价时，首先构建模糊影响图的关系层，确定独立结点以及非独立结点；然后确定频率模糊集，构建模糊影响图的数值层和函数层[9]；最后依据模糊集合理论对独立结点和非独立结点进行评价，得出各价值结点的累积概率分布图，从而直观表述出各类外部影响因素的评估结果，找出关键影响因素并给出可行建议.

2 外部影响因素

高速列车的安全运营除依赖于列车本身各构件的技术性能外，外部因素对其运行的可靠性也有相当程度的影响.

人员因素是比较关键的影响因素，其包括列车操纵人员、检测维修人员及调度指挥人员等.列车管理与使用人员的技术水平、责任意识、生理状态和心理素质等直接影响列车正常工况下的安全运行，在处理紧急情况时，还将决定人员处理事件的决策能力、应急能力等，从而对列车传动系统运行的可靠性产生重要影响.

基础设施的状态直接影响高速列车的安全运行，其包括高速列车的运行轨道、供电系统、信号系统以及通信系统等.高速列车的运行轨道需具备足够的强度、平顺性及一定的弹性，以有效降低外部激扰产生的振动，提高列车传动系统运行的可靠性.另外，在确保供电系统、信号系统及通信系统保持良好的技术状态下，高速列车的传动系才能运行可靠，从而保证高速列车实现安全可靠的运行.

环境因素主要考虑高速列车运行过程中列车内部的噪声、湿度、温度和列车外部的气候条件及地质条件等.高速列车的内部作业环境对工作人员的心理状况、疲劳程度等都会产生影响，从而影响列车传动系统运行的可靠性.高速列车外部的气候条件变化及实际的地质情况会影响传动系统的结构部件及关键设备的运行可靠性，为保证列车本身的可靠性及运营的安全性，不可忽视外部自然环境的影响.

检修制度对保证列车的安全运行也起到至关重要的作用.严谨的检修制度能够保证对高速列车传动系统的合理保养和妥善维修，从而为高速列车传动系的可靠运行提供保障.

在高速列车系统中，管理水平的高低决定了人员配置是否合理、人员的工作效率和工作质量是否达标、设备能否如期保质的维护、列车的运行软环境能否优质可靠.人员及设备管理制度的制定和执行、安全教育等都对列车的运营和保养起到非常关键的作用：人员机构的合理设置可以保证高速列车系统各部分的协调高效工作，从而保证高速列车的安全运营；合理制定管理制度并高效严格执行管理制度可以对产品本身质量进行严格把关，保证各个工作环节执行的最优化；安全教育可以提高列车管理与使用人员的安全意识水平，从而降低列车的运营风险.这些因素都将直接或间接地影响列车传动系统的可靠性.

3 FID 评价理论

3.1 模糊集合

论域U上的模糊集合A可定义为[6]

3.1.1 模糊集合运算理论

模糊集合的运算包括交集、并集、补集计算.

设A、B为论域U上的两个模糊子集合：

（1）设C为A与B的交集，对x∈U而言，有

（2）设D为A与B的并集，对x∈U而言，有

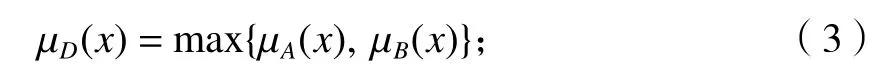
（3）若A与B互为补集，则对x∈U而言，有

式（1）～（4）中：μA(x)、 μB(x)、 μC(x)、 μD(x)分 别 为x隶属于模糊集合A、B、C、D的程度，即隶属度.

3.1.2 模糊关系运算理论

模糊关系主要用来表示元素之间关联程度的大小[4].设U、V为两个模糊集合，R⊆U×V，称R为从U到V的一个二元关系，U×V为模糊集合的直积运算[7]，如式（5）所示.

式中：i=1,2,···,n；j=1,2,···,m.

μR(ui,vj)为（ui，vj）隶属于模糊关系R的程度，后同理，且定义如式（6）所示.

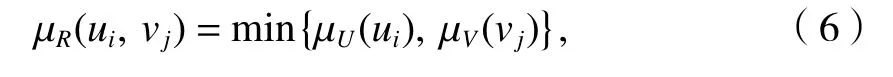
式中：μU(ui)、μV(vj)分 别为ui、vj隶属于模糊集合U、V的程度.

若U、V均为有限集合，其模糊关系R可用式（7）的模糊矩阵来表示[10].设R和S分别表示论域U×V和V×W上的模糊关系（W为有限集合），Q表示U×W上的模糊关系，则R对S的合成即为Q，表示为R◦S[7].对任意的ui∈U,vj∈V,w∈W，Q的隶属函数如式（8）所示.

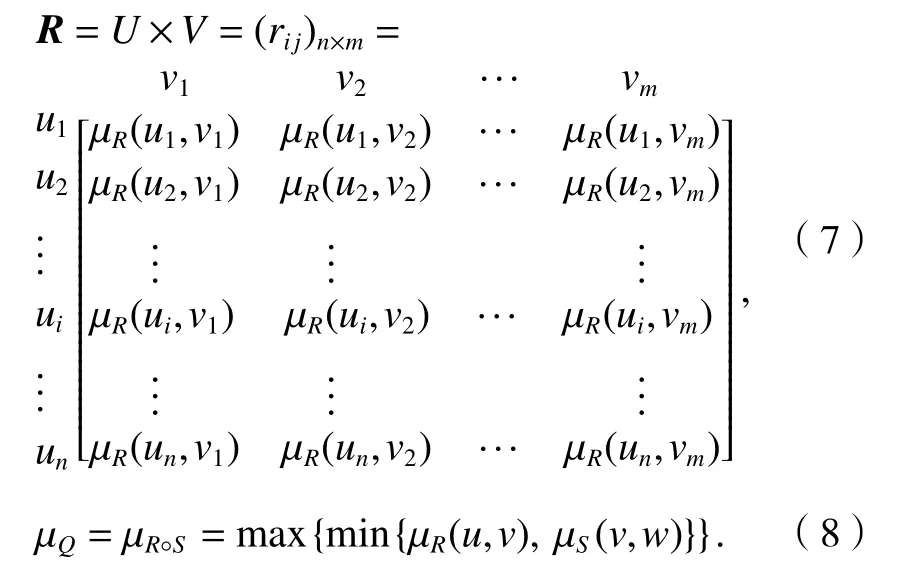
3.2 独立结点的评估

假设N为独立结点，一共有P1～Pn种可能状态，构成可能状态向量为

独立结点N的频率向量为

式（9）、（10）中：Pi为 人为定义的模糊集；fi为每一种可能状态所对应的模糊频率[11].

独立结点N的频率矩阵为

3.3 非独立结点的评估

设非独立结点M及其s个 紧前结点为K1、K2、K3、···、Ks，设FMK为其所有紧前结点的频率矩阵的合成，则

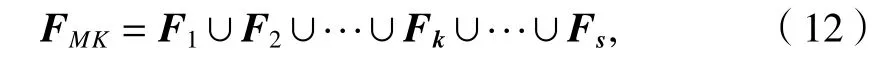
式中：Fk为每一个紧前结点i的频率矩阵，k=1,2,···,s.

设Rk为紧前结点到非独立节点M的一个模糊关系，则所有紧前结点模糊关系R1、R2、···、Rs的合成为

由此非独立节点M的频率矩阵为

根据节点之间的层级关系对前面列举的各项外部因素结点的频率矩阵进行计算，由此得到价值结点的频率矩阵，将该矩阵中各行之和与所对应的频率进行乘积运算[8]，各主要外部因素结点的随机隶属度数值取乘积最大值的一行[12-14]，从而得到主要外部因素结点的发生概率为

式中：mj为 非独立节点第j种状态；μmj为该状态下的隶属度.

4 外部影响因素的评估

4.1 结点模糊集合的确定

（1）确定频率模糊集合

针对本文的研究对象，根据70 份有效独立的专家问卷结果统计分析，分别定义L、I、H、VL、VH表示低、中、高、非常低、非常高，定义频率模糊集合及隶属度如下：

（2）确定状态模糊集合

考虑到各影响因素建模的方便性及评估过程的计算性，定义结点的4 种状态分别为优、良、中、差，其集合分别用E、G、M、B来表示，结点的状态及相应的状态模糊集合如下：

采用幅度变化的百分比来描述中间结点的状态空间，对[-50%，50%]的变化范围11 等分（其中+、-分别表示幅度的增、减），确定频率变化集合如下：

由此定义HD、MD、NO、MI、HI分别表示减少很多、减少较多、无明显变化、增加较多及增加很多，确定非独立结点的状态模糊集合如下：

4.2 建立FID 层次

（1）建立关系层

FID 中的关系层可以直观的将各个结点之间的相互关系表达出来，FID 关系层确立的是否合理直接影响各外部影响因素的评估[15].本例中FID 的核心为CHR3 型高速列车传动系统可靠性，对各类外部因素进行细致划分，从而确定各类外部因素的局部影响图，由此得到传动系统可靠性的FID 关系层，并对各节点进行编号，传动系可靠性的FID 关系层及节点编号如图1所示.

图1 传动系统可靠性的FID 关系层Fig.1 FID relation layer of the reliability of the transmission system

（2）构造数值层

通过数值层来描述各个独立结点的模糊状态及其发生频率之间的关系.独立结点通过频率模糊集和状态模糊集进行数值结构的描述.如图1所示，创建的FID 关系层中共有独立结点16 个，每个结点对应的状态及模糊频率构成了独立结点的数值层，如表1所示.

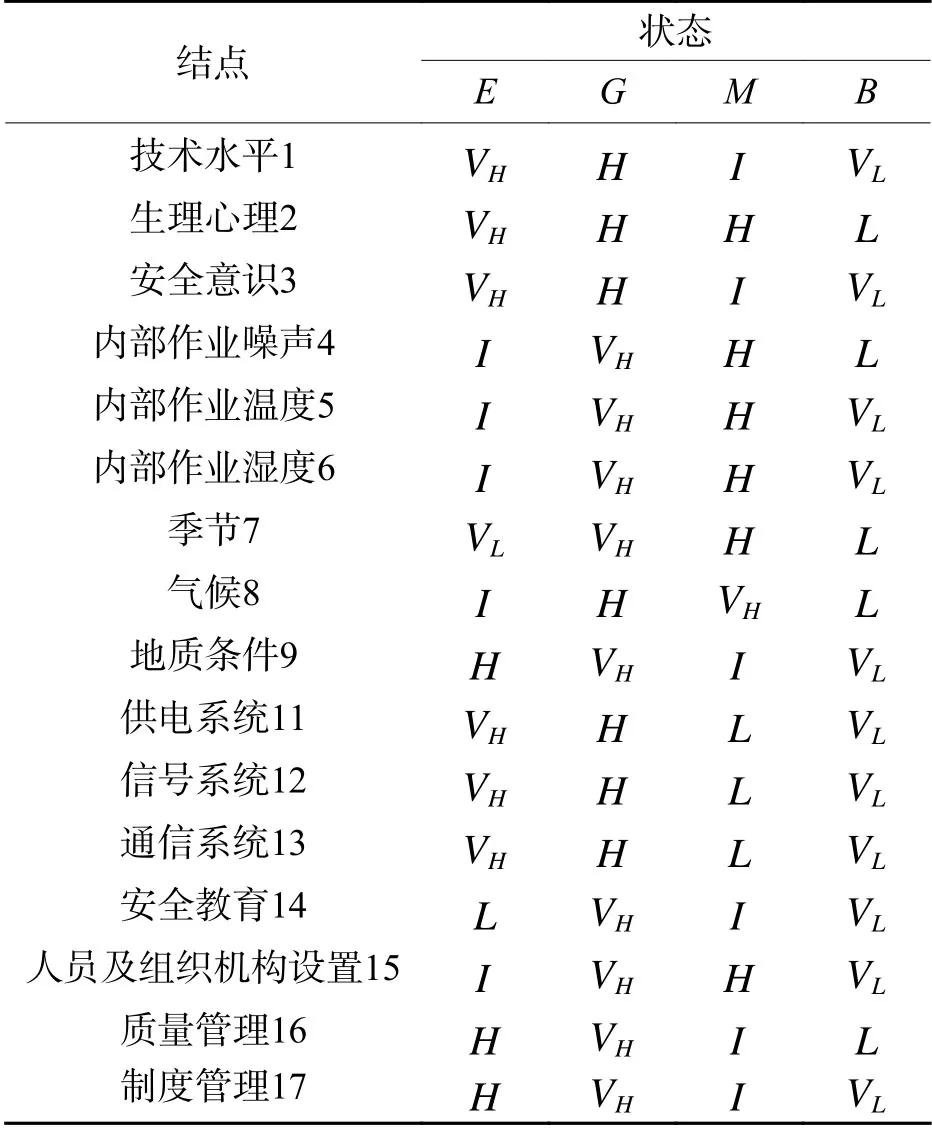
表1 独立结点的数值层Tab.1 Numerical layer of independent nodes

（3）建立函数层

非独立节点评估的基础是FID 的函数层，其可以表述出结点间的模糊关系.按照前面确定的FID 层级关系，通过语言来描述非独立节点的模糊状态与其紧前独立结点的模糊状态关系.根据专家有效调查问卷确立的函数层，限于篇幅，仅列举结点2 与其相关结点20、21 的模糊关系如表2所示.

表2 结点变量间的模糊关系Tab.2 Fuzzy relationship between the node variables

4.3 外部影响因素的评估

以非独立结点22 为例说明计算过程.

（1）独立结点频率矩阵的确定

根据前面创建的数值层，依据结点4 的模糊状态及相应的频率数值.

构建结点4 的频率矩阵为F4，如式（16）.

同理，可得独立结点5 和独立结点6 的频率矩阵为F5、F6，如式（17）.

（2）非独立节点的频率矩阵

由式（16）、（17），非独立结点22 的频率矩阵为F22，如式（18）.

非独立节点22 与其紧前节点4、5、6 的模糊关系为F4-22、F5-22和F6-22，分别如式（19）、（20）.

非独立结点22 的模糊关系矩阵的联合为

式（19）～（21）中：

R4-22、R5-22、R6-22分别为结点4、 5、 6 与 结点22 的模糊关系.

故非独立结点22 的频率矩阵为

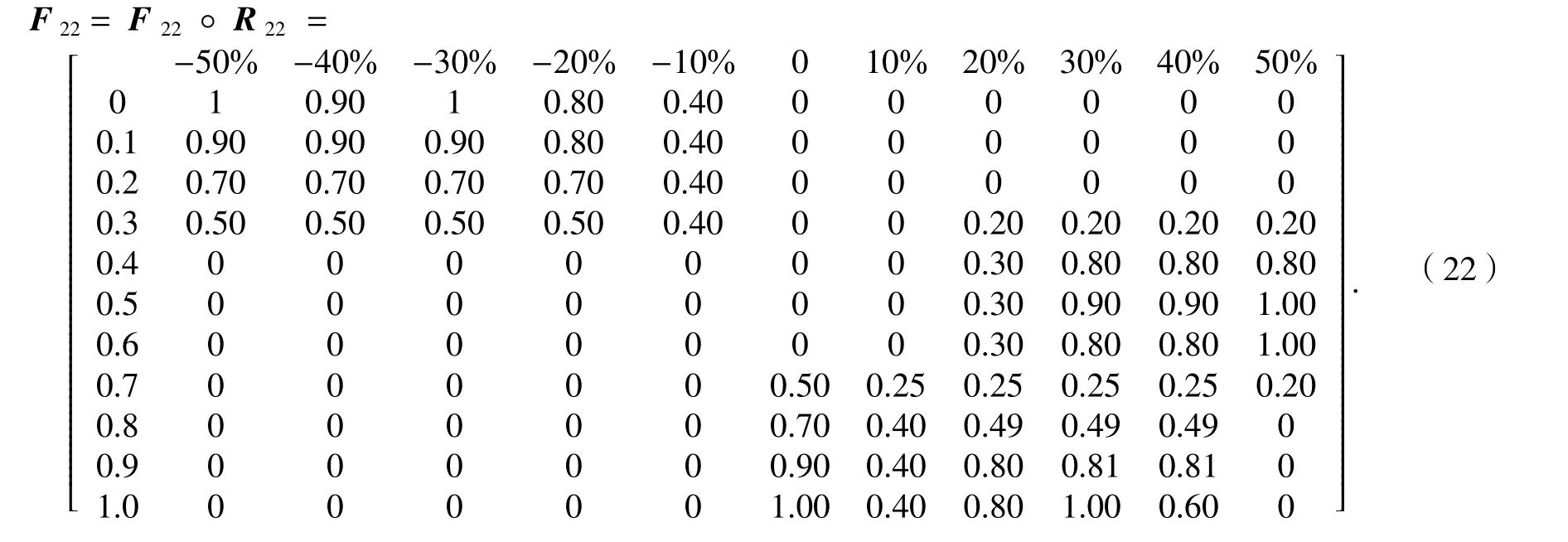
同上可得其他5 个非独立节点的频率矩阵.节点20～26 的发生概率如表3所示.依据表3中的数据可得到累积概率分布图，如图2所示.

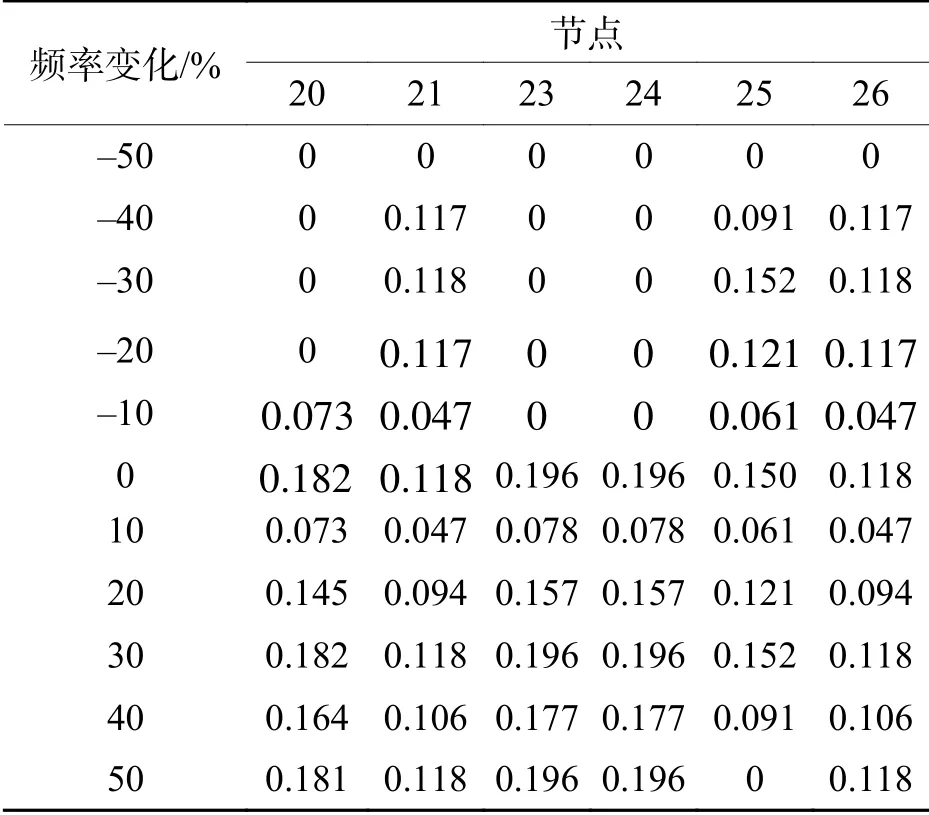
表3 随机结果的概率Tab.3 Probability of random results

由表3及图2可知：

（1）结点23 和结点24 状态频率降低的概率为0，说明这两个结点所代表的外部环境因素与基础设施因素状态稳定；这两项因素在保持当前状态基础上累积提高30%的概率为62.7%，所以加强外部环境监测，并据此调整列车的运行状态，保证高速列车在不同外部环境下的良好运行.此外，定期维护基础设施，保证其有优良的健康状态，对提高传动系的可靠性很有意义.

（2）结点21 和结点25 的随机概率分布比较分散，从数值上来看，与这两个结点所对应的状态降低的累积概率分别为39.9%和42.5%，另外这两项因素在保持当前状态基础上累积提高30%的概率分别为77.6%和90.9%，由图2可以看出二者的概率分布与传动系可靠性的概率分布相近，说明与两节点对应的人员因素与管理因素对传动系可靠性提高的影响非常关键，并具备很大的提升空间.因此列车操纵人员及列车检测维修人员的技能水平应维持在较高水准，同时应提高管理水平.

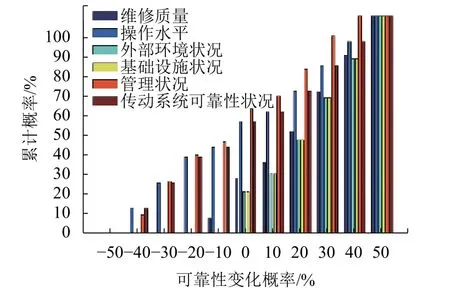
图2 随机结果的累积概率分布Fig.2 Cumulative probability distribution of random results

（3）结点20 所代表的检修质量降低的累积概率为7.3%，其提高30%的累积概率为65.5%，在各外部因素中位列第三，所以强化检修人员的技能水平，完善检修制度对提高传动系的可靠性有很大帮助.

（4）传动系可靠性的随机概率分布结果与人员和管理状况的概率分布相似，表明其受这两方面的影响较大.传动系可靠性降低的累计概率为39.9%，表明其可靠性有较大的提升空间，因此，应针对关键影响因素展开研究分析，以改善传动系的可靠性.

5 结 论

针对影响高速列车传动系可靠性的各类外部影响因素，依据系统工程理论构建传动系统的模糊影响图，结合模糊数学理论对相关的影响因素进行综合分析以及数值计算，表明人员因素和管理因素的状态降低累积概率分布与传动系可靠性分布相似，人员和管理因素是影响待评估传动系可靠性的外部关键因素，可通过提高人员的技能水平，改善具体的管理体制，提高管理效率来提高高速列车传动系的可靠性.

致谢：长春市科技局重点科技攻关项目（14KG031）.