基于相位差谱的非平稳地震波合成及应用
2019-07-11贾宏宇蓝先林郑史雄张永水
贾宏宇 ,蓝先林 ,陈 航 ,郑史雄 ,李 晰 ,张永水
(1.西南交通大学土木工程学院,四川 成都 610031;2.北京工业大学城市与工程安全减灾省部共建教育部重点实验室,北京 100124;3.中铁二院工程集团有限责任公司,四川 成都 610031;4.重庆交通大学土木工程学院,重庆400074)
大跨度结构物的多点地震激励分析能较为真实反映地震作用下各支撑处不同的地面运动,能更加真实地考虑实际地震对长大结构物的作用,从而得到地震作用下更为真实的结构动力响应[1-4].但是,有限的实测地震波根本不可能满足抗震分析的需要,同时也不可能在拟建桥梁的各桥墩处刚好就有实测的地震波,且这些地震波正好能为拟建桥梁的抗震分析所用,这使得人工合成地震波成为天然地震波必要的补充[5-6].
对人工地震波合成,许多学者提出了各种方法,如三角级数法[7-9]、ARMA 方法[10]、小波变换法[11]等,其中三角级数法应用最为广泛[12].三角级数法假设相位角在[0,2π]内均匀分布,从而使得三角级数法只能依靠包络函数来模拟地震动的强度非平稳性[13],纵所周知,人为选择强度包络函数具有任意性,故所生成的地震波表征的强度非平稳性也具有任意性.地震动的非平稳性除了强度非平稳性以外,还具有频率非平稳性.但是,频率非平稳性在三角级数法中不能得到体现[14].基于上述原因,提出关于相位差谱的地震波合成方法,而且这种方法能很好地考虑地震动的强度非平稳和频率非平稳性[15-16].此外,天然地震动又具有空间性和多维性.就目前关于相位差谱合成地震波的研究而言,几乎没有相关研究考虑地震动的多维性.为了能更好地模拟地震动的真实特性,本文基于相位差谱合成了多维多点非平稳地震波,能弥补天然地震波的不足,也为抗震规范人工波合成提供理论参考.
本文基于随机振动理论,模拟多维多点地震动场,基于三角级数法,推导了基于相位差谱合成非平稳地震波的理论,并分析了相位差谱的分布规律,最后以某刚构桥为依托,运用合成的非平稳地震波对刚构桥进行了地震响应分析,并与反应谱法进行对比,验证其正确性和精度.
1 多维多点人工地震动模拟
1.1 多维多点地震动场
为了表示结构m个地面支撑点处的地震激励的相互影响,用加速度表示的互功率谱矩阵为
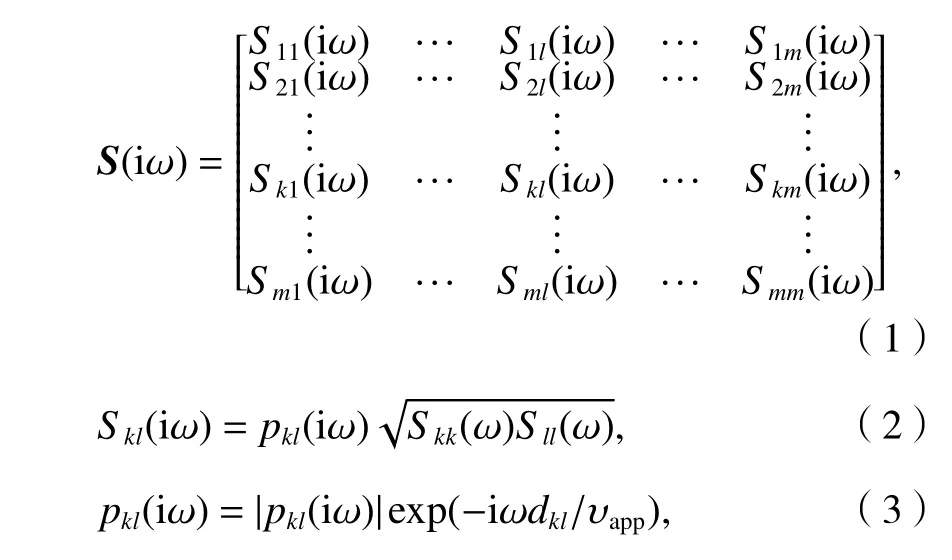
式中:矩阵主对角元素Skk(iω)表示任意点k处的自功率谱密函数;非主对角元素Skl(iω)表示任意两点k、l的互功率谱密度函数;pkl(iω)表示相干函数;|pkl(iω)|表示相干函数的模,反映部分相干效应;相干函数的指数部分- ωdkl/υapp表示相干函数的幅角,相位体现地震空间性中的行波效应;dkl表示支撑点k和l之间的水平距离沿波的传播方向的投影;υapp表示视波速,在实际地震中,视波速随频率变化,离散性较大.
在桥梁抗震分析中,取多个确定的视波速分别计算,其结果能包络视波速离散性的影响,所以在考虑行波效应的抗震分析中,取多个视波速是必要的,也是合理的.
为了研究地震动的多维性,将一维功率谱密度函数矩阵(式(1))中每一个元素按式(4)扩充为三维互功率谱谱密度函数矩阵.
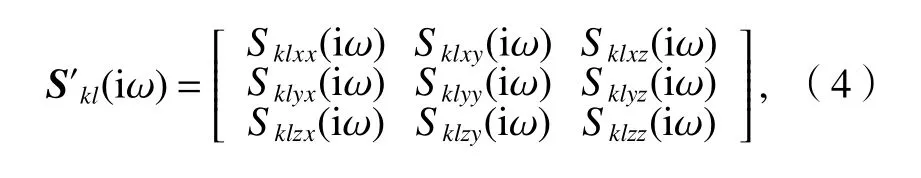
式中:x、y和z分别表示两水平向分量和竖直向分量.
各分量之间有一定比例关系,根据文献[17]:水平分量各个自功率谱密度相同且相关,则可得到

竖直分量的互功率谱也可根据式(6)获得.
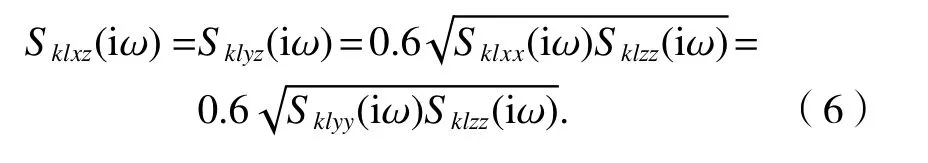
将式(4)、(5)和(6)代入式(1),将只考虑一维(m×m)地震激励的互功率谱密度函数矩阵扩展到了能同时考虑3 个方向地震激励相互影响的三维(3m× 3m)的互功率谱矩阵.
1.2 三角级数法合成多维多点地震动
三维的地震加速度互功率密度函数矩阵是Herrmite 矩阵,而且是正定矩阵.根据式(7),对三维互功率谱矩阵进行LDLT 分解,即

式中:P为3m×r的矩阵,r为矩阵S(ω)的秩.
P*为3m× 3m维矩阵,用lm'(iω)表示x、y和z方向中任意方向在P*矩阵中非主对角的元素,那么地震动的幅值am'和相位角θm'计算方法为
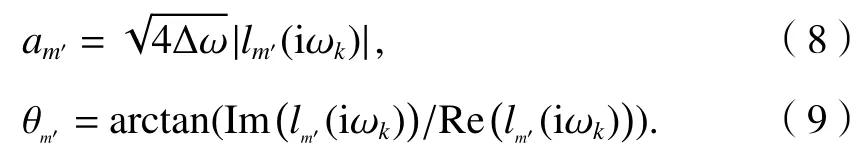
在合成第m′点任意方向dx、dy和dz的平稳地震动时,本文考虑了第m′点任意方向地震动与另外任意点各方向的相关性,那么,第m′点dx或dy、dz方向平稳地震动表示为

式中:am′b和 θm′b分 别为点m′与b在第k个频率时的幅值和相位角;φbk为点m′与b在第k个频率成分中的相位变化值;t为时间.
采用三角级数法合成人工地震波时,φbk为[0,2π]区间内均匀分布的随机变量.运用包络函数模拟地震动非平稳性中的强度非平稳,但是强度包络函数的选择具有很大的任意性,也不能考虑地震动的频率非平稳性.真实地震动具有强度和频率双重非平稳性,双重非平稳性与相位差有着密切的关系,因此,采用相位差谱合成人工地震波更能表征地震动的双重非平稳性.
2 地震动相位差谱
2.1 相位差谱和脉动相位差谱
Ohsaki[15]认为实际地震动的相位谱是随机变量,且具有一定相关性,并用相位差谱的形式来表示其相关性.相位差可表示为

式中:Δφ(f)为相位差,其定义域为[-2π,0],若其值大于0,则减去2π 转换至定义域内;φk和φk+1为相邻两个频率对应的相位角;f为频率.

文献[18]对真实强震加速度记录的相位差谱进行研究,回归得到均值函数Δ(f)为
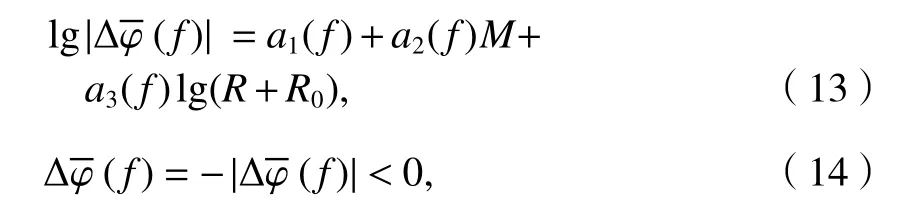
式中:M为震级;R为震源距;R0为常数,其值取15;a1(f)、a2(f)和a3(f)为与频率有关的回归系数,其取值参考文献[18].
ε(f)的标准差σε根据式(15)计算获得.
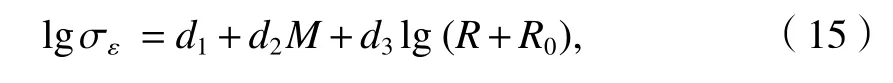
式中:d1、d2和d3为回归系数,当处于岩石地基时,d1=0.089,d2= -1.124,d3= 0.316.
图1给出了震距R= 100 km,不同震级时相位差谱均值变化规律.

图1 相位差谱均值趋势曲线Fig.1 Mean curve trend chart of phase difference spectrum
2.2 相位差谱的分布律
为了研究相位差谱的分布规律,对常用的实际地震波中的El Centro 波S00E 脉动相位差谱进行频数分析[18],得出随机变量εb满足对数正态分布规律,即随机变量εb取对数有 εc=lnεb,那么εc服从正态分布:

则 εb满足式(17)形式的对数正态分布:
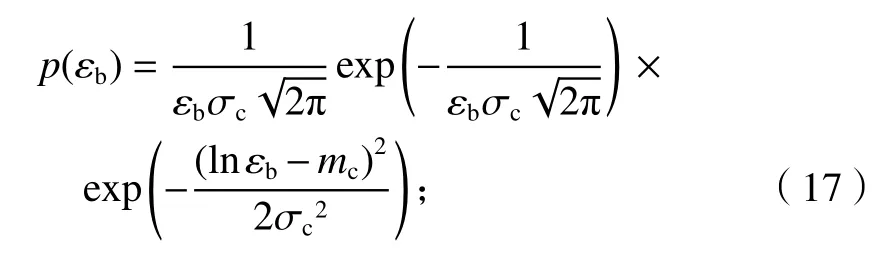
随机变量εc与εb的均值、均方差有如下关系:
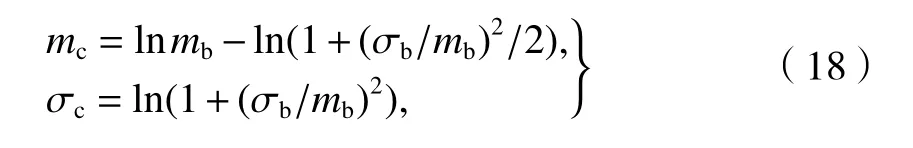
式(16)~(18)中:参数mc、σc分别为随机变量εc的均值和均方差;mb、σb为εb的均值和均方差.
2.3 基于相位差谱的人工地震动合成
均值mb= 2π,σb可根据式(15)回归得到,再根据式(18)获得εb的均值和均方差.最后根据分布规律计算得到满足相应条件的随机数εb,从而就得到脉动相位差ε(f),即

再将ε(f)与式(13)得到的 Δ(f)相加,并结合式(10),就合成了非平稳人工地震动.
3 实际算例
为了说明本文方法的正确性和准确性,采用传统反应谱法来进行验证工作.以某高墩刚构桥(89 m +160 m + 89 m)为对象.该桥位处6 级震区,震源距200 km.首先,选择对应的设计反应谱,特征周期Tg= 0.3 s,
抗震重要系数Ci= 1.7,场地系数Cs= 0.9,阻尼调整系数Cd= 1.0,加速度峰值A= 0.15g,0.20g,反应谱最大值Smax= 2.25CiCsCdA,场地类型为I 类场地,转化为功率谱并模拟地震动场(纵向、横向和竖向地震波传播速度分别为300、500、400 m/s);然后基于相位差谱合成多维多点地震波(地震动持续时间为50 s),再迭代修正合成地震波;最后得到满足精度的人工地震波.本桥两桥墩底处(1# 墩和2# 墩)设计反应谱的最大值分别为0.15g和0.20g,见图2.
3.1 非平稳地震动合成及修正
首先将设计反应谱视为目标反应谱,且转为功率谱,构造具有多维性和地震动空间性的互功率谱矩阵,基于式(10)和式(20)合成多维多点非平稳地震动时程.为了提高合成精度,对合成的地震动进行修正.在频域内,对合成地震动的幅值进行迭代修正.修正方法和步骤如下:
步骤1将合成地震动时程转化为反应谱,并与目标反应谱做商,即
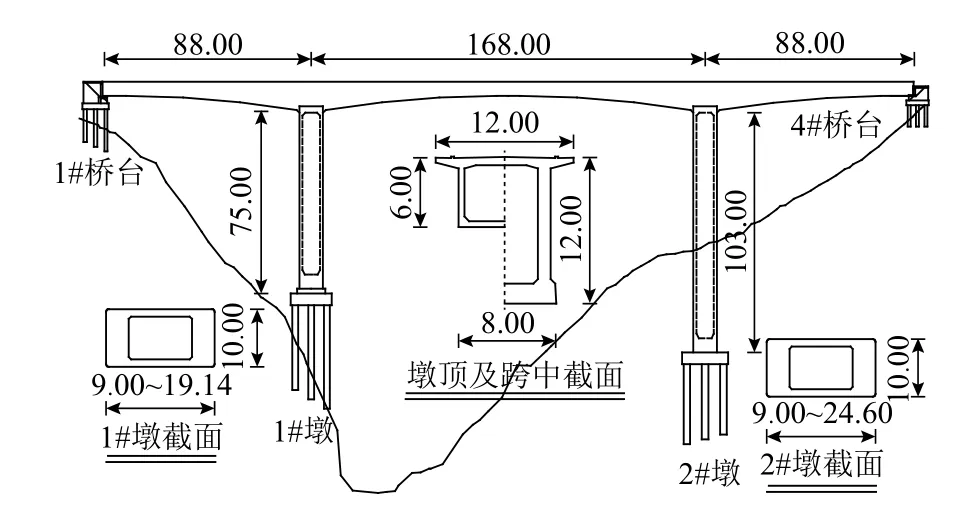
图2 连续刚构桥示意(单位:m)Fig.2 Schematic diagram of continuous rigid frame bridge(unit:m)
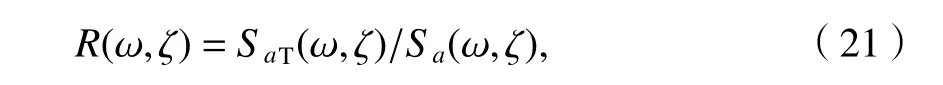
式中:SaT(ω,ζ)为目标反应谱;Sa(ω,ζ)为合成地震动转化的反应谱;ζ为阻尼比.
步骤2精度不满足要求,进行幅值修正,再次合成地震动.
根据式(18)对幅值进行修正.
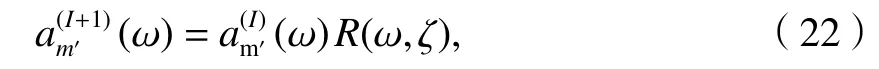
步骤3转到第1 步进行反应谱对比,如满足精度,则跳出此步骤,不满足就进入第2 步.
经上述流程,人工合成桥梁墩底处初始(未迭代修正)多维多点非平稳地震动见图3~5.同时,本文也给出初始合成的人工地震波转化成的反应谱与目标反应谱的对比,见图6.
由图3~6 可知:(1)从波形来看,基于相位差谱合成的多维多点非平稳地震动符合实际地震动非平稳性的3 个阶段:增幅阶段、平稳阶段和衰减阶段;(2)从幅值来看,1# 墩底合成地震动幅值比2#墩地震动幅值大,这与两墩底的目标反应谱峰值对应,可从宏观判断地震波合成是否正确;(3)1# 墩和2# 墩底处初步合成地震动转化的反应谱和目标反应谱基本一致,但1# 墩处幅值最大值相差约40%,2# 墩处相差约57%,且拟合反应谱尖峰较多,不平滑,未达到目标拟合精度15%.为了提高精度,需进一步迭代修正.根据式(18)对初次合成的人工非平稳地震动时程进行幅值修正,并再次对比拟合反应谱和目标反应谱,其最终修正的人工非平稳地震动曲线见图7,最终拟合反应谱与目标反应谱的对比见图8.基于MATLAB 采用Duhamel 积分将新生成地震波转换为拟合反应谱,相关参数:阻尼比为0.05;积分时间步长为0.02 和周期为0~10 s.由于篇幅有限,此处仅列两个桥墩处x方向人工合成的任意地震波对应反应谱和目标反应谱的对比.由图7和图8可知,经过迭代合成的地震动同样具有前述非平稳特性,且在1# 墩和2# 墩处幅值最大值相差分别变为了约6%和13%,且拟合反应谱尖峰较少,曲线平滑.同时,经过两个墩处地震动合成发现,目标反应谱峰值越大,拟合后峰值相差也越大,如2#墩处目标反应谱峰值0.2g,拟合反应谱与目标反应谱差值比1# 墩处大.修正后1# 墩和2# 墩处的地震动幅值缩减最大值分别为0.745 m/s2和1.580 m/s2.

图3 x 方向非平稳地震动(未修正)Fig.3 Non-stationary ground motion at x direction(uncorrected)

图4 y 方向非平稳地震动时程(未修正)Fig.4 Non-stationary ground motion at y direction(uncorrected)

图5 z 方向非平稳地震动(未修正)Fig.5 Non-stationary ground motion at z direction(uncorrected)

图6 拟合反应谱和设计反应谱(未修正)Fig.6 Fitting response spectrum and design response spectrum(uncorrected)
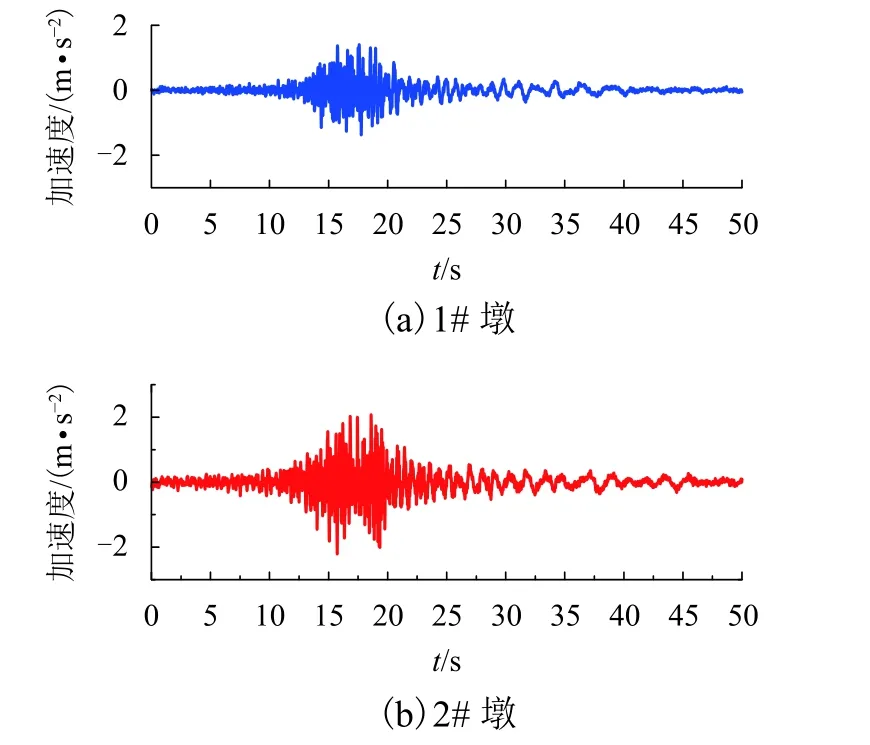
图7 x 方向的非平稳人工地震时程(修正)Fig.7 Non-stationary ground motion at x direction(corrected)

图8 拟合反应谱和目标设计反应谱(修正)Fig.8 Non-stationary fitting response spectrum and target design response spectrum(corrected)
3.2 桥梁地震响应分析
为了进一步研究修正前与修正后地震波对桥梁结构动力响应的影响,也为验证人工合成地震波的正确性.在图2刚构桥对应的有限元模型中,在1#墩和2# 墩底基础处分别施加合成的非平稳人工地震动,对桥梁结构进行多点激励分析.图9是基于本文合成地震动的时程分析法和传统反应谱法的工况说明图例.图9中列出了5 种工况:工况1,1# 墩和2# 墩峰值加速度都为0.15g时程分析法(一致激励);工况2,1# 墩和2# 墩峰值加速度分别为0.15g和0.2g时程分析法(多点激励);工况3,1# 墩和2# 墩峰值加速度都为0.2g时程分析法(一致激励);工况4,1# 墩和2# 墩峰值加速度都为0.15g反应谱法(一致激励);工况5,1# 墩和2# 墩峰值加速度都为0.2g反应谱法(一致激励).图中:UE 为一致激励;PDS为相位差谱法;ME 为多点激励;RS 为反应谱法.
图10~12 给出了各工况荷载作用下,刚构桥墩底剪力和弯矩的对比情况,由图10可知,加速度峰值越大,墩底的剪力和弯矩值也越大,初步判断地震作用下结构响应规律符合实际情况.采用反应谱法比基于相位差谱合成地震动的时程方法(本文方法)计算得到的剪力和弯矩要大,当加速度为0.2g时,1# 墩的剪力最大相差约3 973.5 kN,2# 墩的弯矩值最大相差889 146.2 kN·m;2# 墩比1# 墩剪力值小,但2# 墩比1# 墩弯矩值大,其中采用反应谱法计算的剪力值相差在10%以内,弯矩值相差在17%以内,采用本文时程分析法计算的剪力值相差在9%,弯矩相差在12%以内.这说明了本文方法和传统反应谱法计算结果基本一致,也说明了本文方法正确性.

图9 连续刚构计算工况图例Fig.9 Analysis case of continuous rigid frame bridge
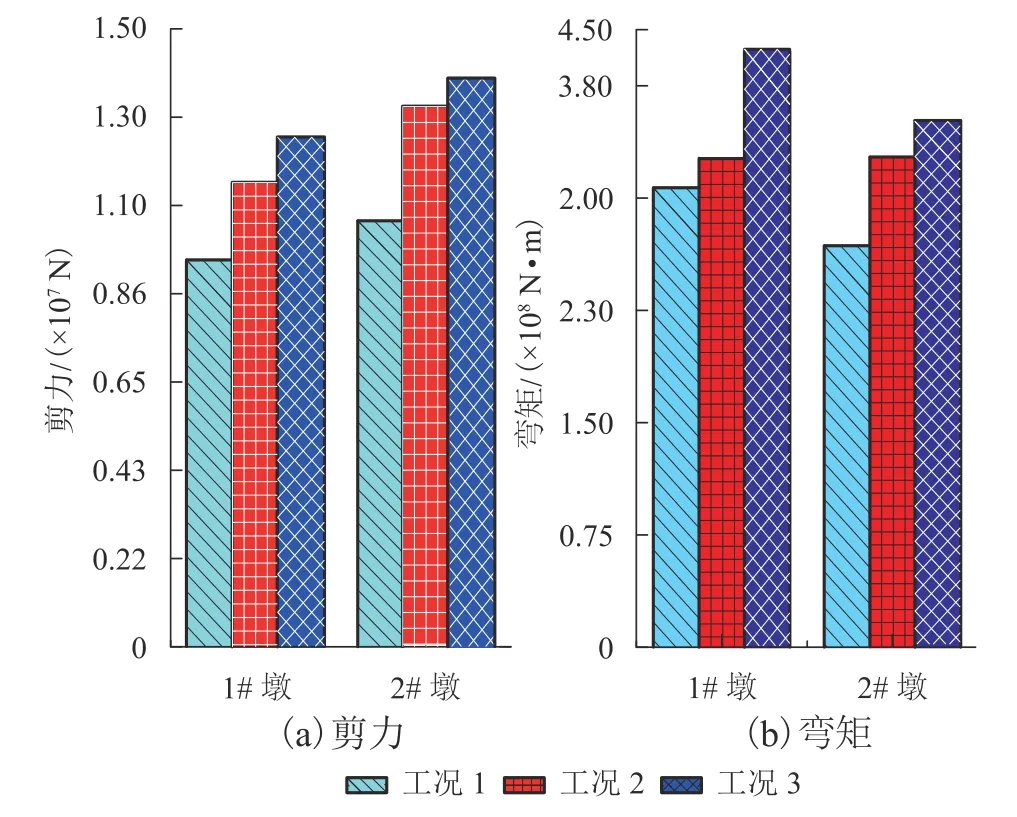
图10 一致激励与多点激励的墩底剪力弯矩(相位差谱法)Fig.10 Shearing and moment at the bottom of the piers under UE and ME(phase difference spectrum method)
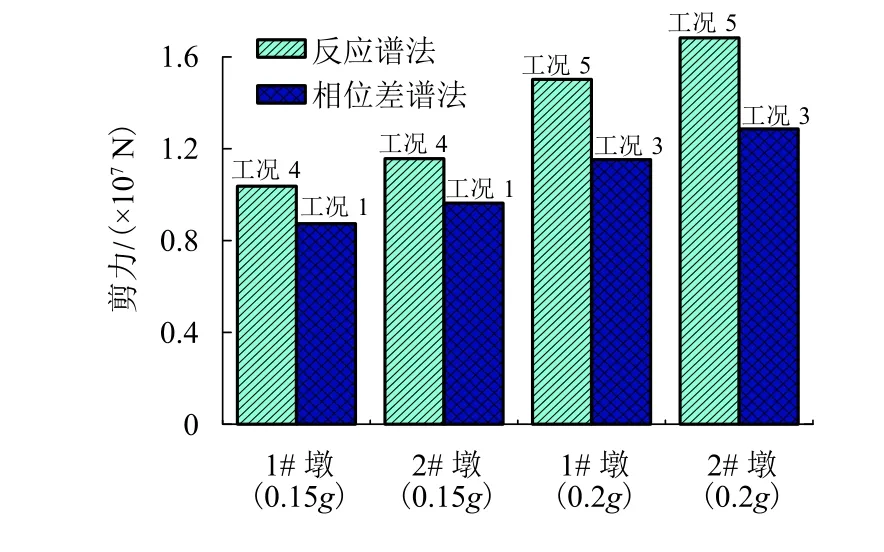
图11 墩底处剪力Fig.11 Shearing of the piers bottom
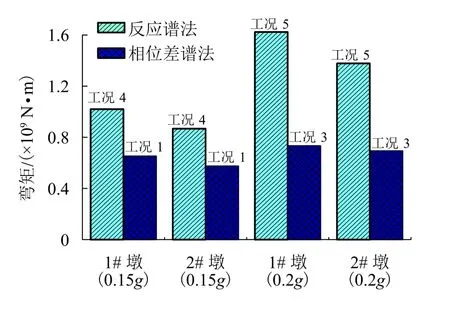
图12 墩底处弯矩Fig.12 Moment of the piers bottom
4 结 论
本文基于相位差谱合成了多维多点非平稳地震动,采用频域方法对合成地震动进行迭代修正.并研究了人工非平稳地震动对刚构桥多点激励下的响应情况.得到如下结论:
(1)基于相位差谱合成的多维多点非平稳地震动不用包络函数控制地震波的波形,较好地排除了人工选择强度包络函数的任意性,优于传统的三角级数法;
(2)基于相位差谱合成多维多点地震动不但考虑了地震动的空间相关性,还考虑了地震动的多维性,更加符合真实地震动特征;
(3)本文方法与传统反应谱法计算结果基本一致,采用反应谱法计算的1# 和2# 墩剪力值相差在10%以内,弯矩值相差在17%以内,而本文时程分析法分别在9%和12%以内.
