一种鼓形齿联轴器的侧隙设计方法

2019-07-11关亚彬杨小辉方宗德向龙陈国定

西安交通大学学报 2019年7期

关亚彬,杨小辉,方宗德,向龙,陈国定

(西北工业大学机电学院,710072,西安)

鼓形齿联轴器主要应用于机械传动系统中,联接主、从动轴,传递转动和扭矩。鼓形齿联轴器在运转过程中,不仅能够承受极大的载荷,而且具备综合补偿鼓形齿和内齿圈轴间倾角的能力。由于这些优点,其往往被用于重载或工况复杂的传动轴连接中,例如船舰[1]、风电[2]及轧钢[3]等的传动系统。

为了补偿轴间倾角产生的相对位移和避免轮齿之间发生边缘接触,鼓形齿联轴器传动较普通圆柱齿轮传动应具有更大的侧隙和齿面鼓形量。因此,国内外学者对鼓形齿联轴器的轮齿接触分析、侧隙设计以及齿面设计展开了大量研究。Nakashima基于平行于端面的截面为连续变位的渐开线的假设,采用齿面离散网格的方法,计算了鼓形齿和内齿圈相邻齿面的间隙量,得到了最小间隙点的位置,以此获得了在相应载荷下,轮齿的接触数目以及轮齿间的载荷分配[4]。在此基础上,Alfares等研究了轴间倾角状态下,模数、压力角、修形量对鼓形齿和内齿圈相邻齿面间最小间隙分布的影响[5],但是得到的最小间隙分布以及最小间隙量与Nakashima不同。Ohshima等采用抛物线逼近鼓形齿齿面的横截面形状,进而表达出了整个齿面的方程,并以成形法加工鼓形齿为例,计算了齿面的间隙分布,并进行了试验验证[6]。Hakozaki等提出了改变鼓形齿沿着齿廓方向曲率的方法,研究结果表明,该方法可以获得更大的承载接触区域和更小的轮齿间隙,降低由侧隙引起的冲击噪声[7]。Guan等采用成形砂轮加工鼓形齿,插齿刀加工内齿圈,建立了鼓形齿联轴器的齿面模型,并进行了轮齿接触分析[8]。刘鹄然等和毛世民等使用铣刀加工鼓形齿,进行了齿面接触分析,并进行了试验验证[9-10]。彭福华等按照共轭曲面原理,推导了共轭鼓形齿联轴器的接触线及齿面方程,分析了在不同倾角下轮齿齿面的接触状态及变化规律,并进行了滚检试验[11-13]。易传云等建立了非共轭齿面的鼓形齿联轴器齿面方程,根据连续切触方程进行了啮合分析,得出了啮合过程中的传动误差曲线,并求解了齿面的诱导法曲率和相对滑动系数[14-16]。李月潭等基于沿位移圆方向齿廓为渐开线的假设,建立了鼓形齿齿面方程,并推导了鼓形齿联轴器的齿面最小间隙点位置、齿面间隙以及综合曲率半径的计算公式[17]。魏家麒等基于Alfares的网格法进行了轮齿接触分析和力学分析[18]。

从上述文献中可以看出,在鼓形齿联轴器处于轴间倾角的工况下,采用齿面离散网格的方法虽然可以获得相邻齿面间最小间隙的位置和大小,但是这种方法耗时长且计算精度不高,不便用于鼓形齿联轴器的最小侧隙设计。因此,本文基于齿轮啮合原理提出了一种更精确快速的用于鼓形齿联轴器最小侧隙设计的方法。本文研究从以下方面展开:首先,对比了鼓形齿联轴器和圆柱齿轮副的运动规律;其次,建立了鼓形齿联轴器的齿面方程和装配关系;再次,基于连续切触方程,提出了鼓形齿联轴器最小侧隙设计方法;最后,将本文方法与Alfares方法[5]、有限元方法的计算结果进行了对比验证。

1 鼓形齿联轴器和圆柱齿轮副的运动规律对比

鼓形齿联轴器由齿数相等的内齿圈和鼓形齿组成,鼓形齿是齿顶面为球面、齿向为鼓形修形的齿轮,内齿圈是直齿内齿圈。圆柱齿轮副的啮合传动沿着啮合线进行,相较圆柱齿轮副而言,鼓形齿联轴器的运动状态更加复杂,两者的运动规律如图1所示。

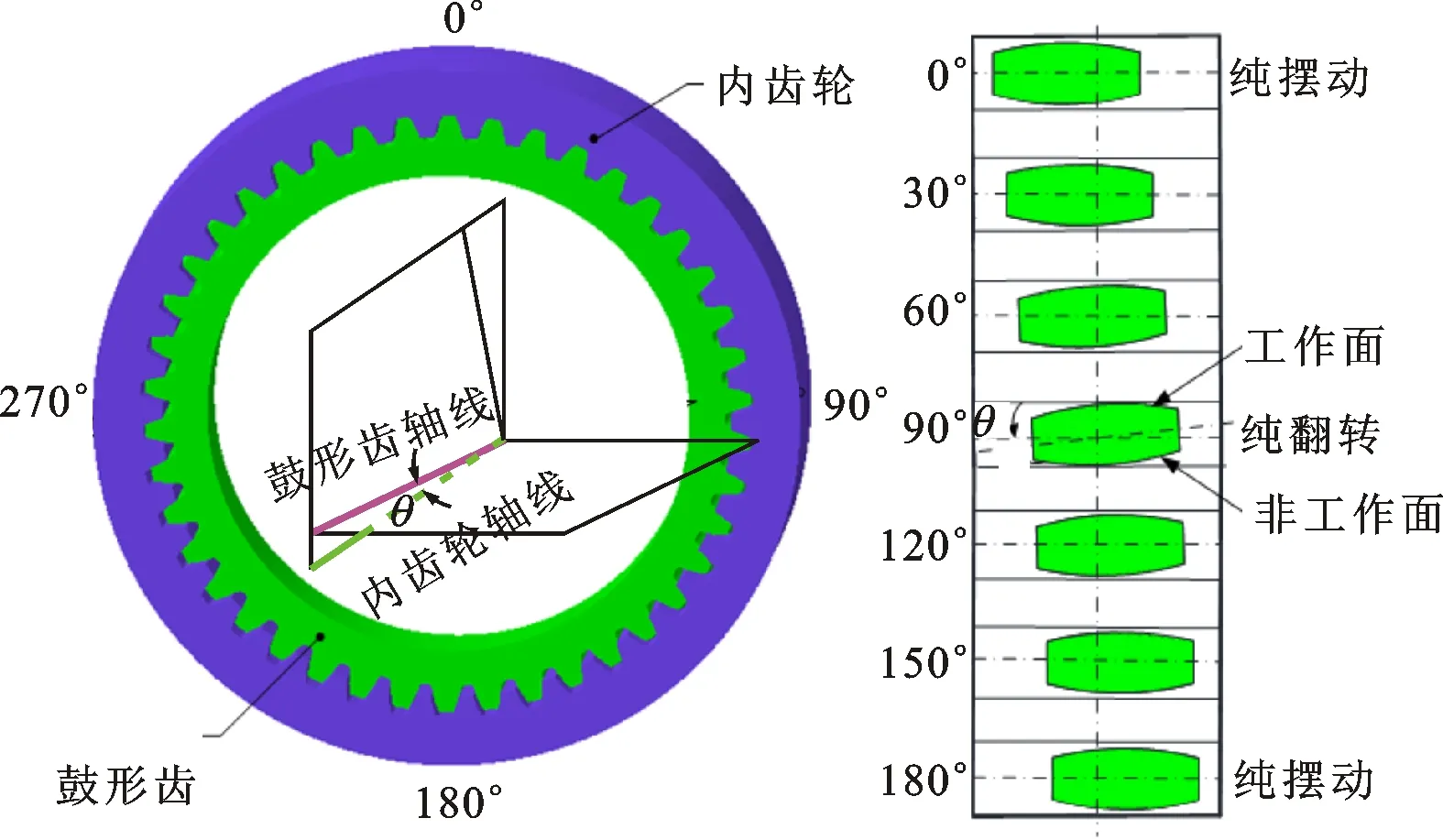
(a)鼓形齿联轴器

(b)圆柱齿轮副图1 运动简图

图1a为鼓形齿联轴器在倾角θ下的运动简图,沿着顺时针方向,把鼓形齿联轴器的运动位置依次规定为转角0°、90°、180°、270°,由于转角相差为180°的轮齿处运动状态是一样的,因此下面只分析0°～180°转角区间内轮齿的运动状态,其运动将经历纯摆动区、摆动和翻转复合区、纯翻转区、翻转和摆动复合区、纯摆动区。从图1a可以看出:在纯翻转区(转角90°),鼓形齿和内齿圈相邻轮齿工作面和非工作面的间隙均达到了最小值;在纯摆动区(转角0°和180°),鼓形齿和内齿圈相邻轮齿工作面和非工作面的间隙均达到了最大值。因此,在进行鼓形齿联轴器侧隙设计的时候,仅考虑纯翻转区的间隙量,便可以保证鼓形齿联轴器在倾角下正常工作。

相比于复杂的鼓形齿联轴器传动,圆柱齿轮副的运动规律更为简单,其运动简图如图1b所示,op和og分别为小轮和大轮的中心点。在传动过程中啮合点P均沿啮合线N1N2方向移动,从图中可以直观地看出正在啮合、即将进入啮合和退出啮合的齿的位置。由于圆柱齿轮副在工作状态下不要求能承受较大的倾角变化,因此很少有学者对圆柱齿轮副的侧隙设计进行研究。

2 鼓形齿联轴器齿面模型

根据沿齿宽方向连续变位产生鼓形齿齿面的方法可知,需要确定的鼓形齿齿面的关键参数就是平行于端面的每个横截面位置的变位系数x。下面叙述参数x的求解过程。

鼓形齿齿面各横截面变位系数之间关系如图2所示。分别以鼓形齿中心oh以及产生鼓形齿齿面的位移圆圆心od为原点,沿着齿宽方向zh、zd和齿高方向yh、yd建立坐标系。Rds为位移圆半径,l为位移圆与中截面的交点和位移圆与任意截面的交点沿着坐标轴yh的距离,Rf为分度圆半径。鼓形齿齿面的任意截面都可以看作是沿鼓形齿轴线方向zh的连续变位修形,lz表示任意截面与中截面之间的偏置距离,x0表示中截面处的齿廓变位系数,x1表示任意截面处的齿廓变位系数,x2表示端面处的齿廓变位系数,e表示位移圆圆心与鼓形齿中心之间的距离。

图2 鼓形齿齿面各横截面变位系数之间关系

根据图2可知,Rds和l可以表示为

Rds=Rf+e

(1)

(2)

由于鼓形齿齿面是由齿廓形状沿着鼓形齿轴线zh连续变位形成的,l和齿轮模数m以及x1、x0之间的关系可以表示为

l=m(x0-x1)

(3)

将式(2)和(3)联立,可以得到任意截面的变位系数x1为

(4)

鼓形齿联轴器的啮合坐标系如图3所示,Sf(xf,yf,zf)为固定坐标系,St(xt,yt,zt)为误差坐标系,Sf1(xf1,yf1,zf1)为辅助坐标系,Sh(xh,yh,zh)和Ss(xs,ys,zs)分别为鼓形齿和内齿圈的固连坐标系。zh和zs分别表示鼓形齿和内齿圈的轴线方向,φh为鼓形齿绕zh轴的转角,φs为内齿圈绕zs轴的转角,ΔE为鼓形齿与内齿圈中心点之间的距离。

图3 鼓形齿联轴器啮合坐标系

在固定坐标系Sf(xf,yf,zf)下,内齿圈和鼓形齿的齿面方程以及法矢可以表示为

(5)

(6)

(7)

(8)

式中:

根据上述鼓形齿联轴器的齿面方程以及鼓形齿和内圈之间的装配关系,建立鼓形齿联轴器的有限元模型以及边界条件,如图4所示。在鼓形齿中心处定义一个单节点六自由度的点单元,将鼓形齿轴孔壁的节点与中心处的点单元刚性耦合,保留旋转自由度,约束其他自由度。对于内齿圈,进行轮缘节点全约束。在点单元上施加绕鼓形齿轴线的转矩T。

图4 鼓形齿联轴器的有限元模型及边界条件

3 最小侧隙设计

侧隙作为鼓形齿的重要设计参数,不仅影响鼓形齿联轴器的装配,而且影响联轴器的动力学性能。侧隙设计量太小,鼓形齿联轴器不能在倾角下正常工作;侧隙设计量太大,轮齿之间的碰撞噪声会变大[4]。因此,本节将给出轮齿在倾角下能正常工作时,鼓形齿联轴器的最小侧隙计算方法。

从第1节可知,鼓形齿联轴器在纯翻转区时,相对于其他区域,工作面和非工作面的间隙均最小,工作面和非工作面的间隙与鼓形齿联轴器最小设计侧隙量呈现负相关。因此,最小侧隙设计时,仅考虑轮齿在纯翻转区的接触状态即可,只要在纯翻区的轮齿不发生干涉,便可以保证其他区域的轮齿不发生干涉。

(a)无倾角 (b)有倾角图5 无侧隙时纯翻转区的轮齿接触状态

要获得无侧隙鼓形齿联轴器在倾角下纯翻转区的最小间隙量,首先要获得最小间隙点的位置。最小间隙点的位置可以通过齿轮接触分析计算获得。

在齿轮啮合过程中,两齿面连续相切接触。由此可知,在固定坐标系Sf(xf,yf,zf)中,任一时刻两齿面间有最小间隙点,且最小间隙点处都有公法线,用数学公式表达为

(9)

根据式(9)可以获得鼓形齿联轴器在纯翻转区最小间隙的位置。

如果式(9)无解或者解的范围超出齿面边界,则认为齿轮发生边缘接触。由于鼓形齿的齿宽比内齿圈小,故不考虑内齿圈端面发生边缘接触的情况。

要判断边缘接触具体发生在哪个边缘,首先需要对齿轮边缘进行离散化处理,计算离散点处对应的齿面间的间隙量,然后通过对比各点的间隙量,判断出哪个边缘处的间隙量最小,再根据边缘接触分析公式计算出边缘最小间隙点的位置。鼓形齿联轴器边缘的离散点如图6所示。以鼓形齿的齿顶和内齿圈的齿面接触为例,最小间隙点的求解公式为

(10)

(a)鼓形齿

(b)内齿圈图6 鼓形齿联轴器边缘离散点

dsh=Rf(φh1-φs1)

(11)

结合图5b和图7可以看出,在纯翻转区,鼓形齿和内齿圈工作面间和非工作面间均有大小为dsh的周向干涉量。因此,要保证鼓形齿和内齿圈在倾角θ下不发生干涉,需使鼓形齿联轴器的最小侧隙C为

(12)

图7 最小间隙量计算示意图

4 算例分析

本节以文献[5]中的鼓形齿联轴器参数为例,运用本文的最小侧隙设计方法,得到了不同轮齿位置处最小间隙点在鼓形齿齿面的轨迹以及一个圆周的最小量分布,并与文献[5]的结果进行了对比。为了验证本文提出的鼓形齿联轴器最小侧隙设计方法的准确性,与有限元计算结果也进行了对比。表1为该鼓形齿联轴器的基本参数。

表1 鼓形齿联轴器的基本参数

将图1中鼓形齿联轴器位于纯摆动区(转角0°)位置的鼓形齿轮齿记为轮齿1,顺时针依次标记为轮齿2、轮齿3,一直到轮齿52。由于Alfares的论文中只给出了8个轮齿位置处最小间隙点形成的轨迹,因此图8和图9分别给出了在倾角0.5°和1°下,这8个位置的鼓形齿齿面最小间隙点轨迹。

对比图8a和8b、9a和9b可以看出:本文方法和Alfares方法得到的最小间隙点轨迹的形状一致,但是某些轮齿的最小间隙点位置不一致,尤其在纯翻转区(轮齿13、轮齿39)附近,最小间隙点距离轮齿边缘更远,二者相距大约1/8齿宽。对比图8a和9a可以看出:随着倾角增大,纯翻转区(轮齿13、轮齿39)附近最小间隙点的位置更接近轮齿端面边缘,更易发生边缘接触,而且大部分轮齿的最小间隙点都处于鼓形齿的齿顶和齿根边缘。

(a)本文方法

(b)Alfares方法图8 倾角0.5°下鼓形齿齿面不同位置最小间隙点轨迹

倾角为0.5°和1°时,鼓形齿联轴器的最小间隙分布如图10所示,可以看出:当倾角为0.5°时,在纯翻转区(转角90°、270°)附近,本文方法比Alfares方法计算得到的最小间隙小5 μm;当倾角为1°时,在纯翻转区附近本文方法比Alfares方法计算得到的最小间隙小40 μm。可见,本文方法计算得到的最小间隙比Alfares方法小,这是因为本文方法更加准确地找到了纯翻转区处的最小间隙点在鼓形齿齿面上的位置。

(a)本文方法

(b)Alfares方法图9 倾角1°下鼓形齿齿面不同位置最小间隙点轨迹

图10 鼓形齿联轴器的最小间隙分布

为了验证本文求解的最小间隙点位置较Alfares方法更加精确,将本文结果与有限元结果进行了对比。顺时针从纯摆动区位置开始对鼓形齿轮齿编号,依次计为轮齿1、轮齿2、轮齿3,一直到轮齿52。鉴于轮齿数目太多,图11中只给出了奇数编号轮齿在扭矩100 N·m下,倾角0°、0.5°和1°的鼓形齿齿面接触应力云图。从图11a中可以看出,0°倾角下,鼓形齿与内齿圈为线接触,这是由于两者在中截面处的齿廓形状相同,同时也说明了本文建立的鼓形齿联轴器齿面模型是精确的。对比图11b和8a、11c和9a得出,倾角0.5°和1°下,本文方法和有限元方法得到的在纯翻转区(轮齿13、39)的最小间隙点均位于距离轮齿端面1/4和1/8齿宽处,说明了本文方法和有限元方法可以获得一致的结果。因此,本文方法比Alfares方法更准确。