青龙沟金矿露天转地下采场矿石贫化评估*

田 军，李怀宾，杨晓明，张姝婧



青龙沟金矿露天转地下采场矿石贫化评估*

田 军1，李怀宾2，杨晓明2，张姝婧2

(1.东北大学 深部金属矿山安全开采教育部重点实验室，辽宁 沈阳 110819；2.东北大学 采矿地压与控制研究中心，辽宁 沈阳 110819)

为了研究采场的贫化问题，提出了一种ELOS(超挖深度)的量化指标，以青龙沟采区北矿段为工程背景，采用Mathews稳定性图法，计算得出上盘超挖深度较小，均小于0.5 m；下盘超挖深度随着采场长度的增加变化为0.7~1.6 m；通过数值计算，采场上盘超挖深度较小且变化不明显，而下盘超挖深度变化较显著，变化范围为0.64~1.07 m。图表法和数值模拟法得出的结果具有一致性，结果表明：在采场开挖时，下盘超挖较严重，应加强采场下盘的支护。

贫化；超挖深度；Mathews图表；数值模拟

矿产资源具有有限性和不可再生性，所以，优化开发矿产资源、降低生产成本以及提高经济效益是矿山的重要目标[1−2]。随着矿产资源产量的逐渐增大，降低开采过程中的损失与贫化对于矿山降低生产成本至关重要。矿山在生产过程中，不正确的采矿方法、开采顺序等都会致使大量的废石混入矿堆，导致矿石贫化率增高，出矿品位相应降低，加大采矿和矿石处理成本；因此，降低贫化率对于提高矿山的经济效益、充分利用矿产资源和延长矿山服务年限具有重要意义[3]。本文以青龙沟采区北矿段为研究对象，采用图表和数值模拟相结合的方法对采场贫化进行分析。

1 现场工程地质

大柴旦矿业有限公司青龙沟采区北矿段上部为露天开采，目前，露天开采已经结束，主要开采青龙沟采区北矿段，即露天转地下部分。青龙沟采区北矿段共探明4条矿体，其中M2矿体规模较大，图1为青龙沟采区三维地质模型。

青龙沟采区北矿段位于青龙沟复向斜的东南段，矿区内褶皱构造和断裂较发育，总体走向为NNW~SSE，与区域主构造方向一致，矿区侵入岩主要为块状构造，中元古代地层为薄~中厚层状构造。青龙沟金矿主矿体(M2)位于16250N-16550N勘探线间，形态呈-东倾的简单板状，向深部延伸时开始出现分支，倾向和走向上具有较好的稳定连续性。矿体上盘为条带状大理岩，下盘为白云质大理岩，矿体为蚀变的变质砂岩。矿化区域厚度一般从数米至二十多米，厚度变化较大，矿体呈似层状和透镜状，倾向NE，走向157°，倾角60°~90°，平均78°左右，矿体平均厚度约10 m。经多年开采，剩余矿体走向长675 m，倾向最大延深174 m。

图1 青龙沟采区三维地质模型

根据青龙沟采区北矿段M2矿体的赋存特点，对急倾斜中厚矿体采用长矿房干式充填采矿法进行开采(见图2)，采场高度设计为20 m，该方法采用深孔连续爆破后退式落矿，对出矿形成的空区进行连续干式充填。该采矿方法的优点是连续爆破落矿、出矿和连续充填空区，即随采随充。理论上，该采矿方法没有采场长度限制，这将减少切割天井数量，达产快、钻孔、循环时间短，提高了劳动生产率，获得了较好的经济效益。

图2 长矿房连续干式充填采矿法

利用测线法对青龙沟采区北矿段矿岩进行结构面调查分析，根据岩石力学实验和现场调查，采用Q、RMR和GSI分类方法对矿岩质量进行评价，最后利用经验公式获得矿岩力学参数[4]，如表1所示。

表1 岩体力学参数

2 矿石贫化主要影响因素分析

导致矿石贫化的影响因素很多，通常贫化是这些因素共同作用的结果。这使得很难检测单一变量对贫化的影响。影响矿石贫化的主要原因可以分为3大类：钻孔和爆破问题，不合适的采场尺寸设计和地质条件问题。

2.1 钻孔和爆破

钻孔和爆破问题包括钻孔精度和单位耗药量。钻孔精度是由于钻孔位置、钻孔倾角、钻孔偏斜和钻孔长度错误等造成的。钻孔和爆破问题对矿石贫化的影响很难预测，因为没有足够的数据来比较钻孔精度和超挖深度之间的关系。此外，钻孔的不良性能也会导致各种各样的结果，包括钻孔损失、钻孔间距的变化等。图3显示了钻孔精度差的可能影响，蓝色是计划中的钻孔，红色是可能错误的钻孔。由于这些钻孔误差作用的持续累积，爆破的对称性也会发生变化，可能导致矿石贫化或矿石损失。

图3 钻孔精度的影响

2.2 采场尺寸设计

由于采场尺寸设计造成的贫化，意味着采场边界的确定使得贫化几乎是不可避免的，当采出的矿量相同时，采场尺寸可以设计成不同情况，矿石贫化也会随之变化。

2.3 地质条件

地质条件主要包括地应力和采场围岩条件，矿石贫化通常是由这2个因素相互作用造成的，如软弱岩体的垮塌、冒落等。地质问题与采场尺寸设计密切相关，因为良好的采场尺寸，可以减小矿石贫化程度。

3 矿石贫化评估

在开采过程中，矿石贫化是不可避免的。贫化又分为计划内贫化和计划外贫化。计划外贫化是由采场冒落或围岩混入而导致的，计划内贫化则是由包含在矿体内或采场边界范围内随回采而混入的废石造成的(见图4)。

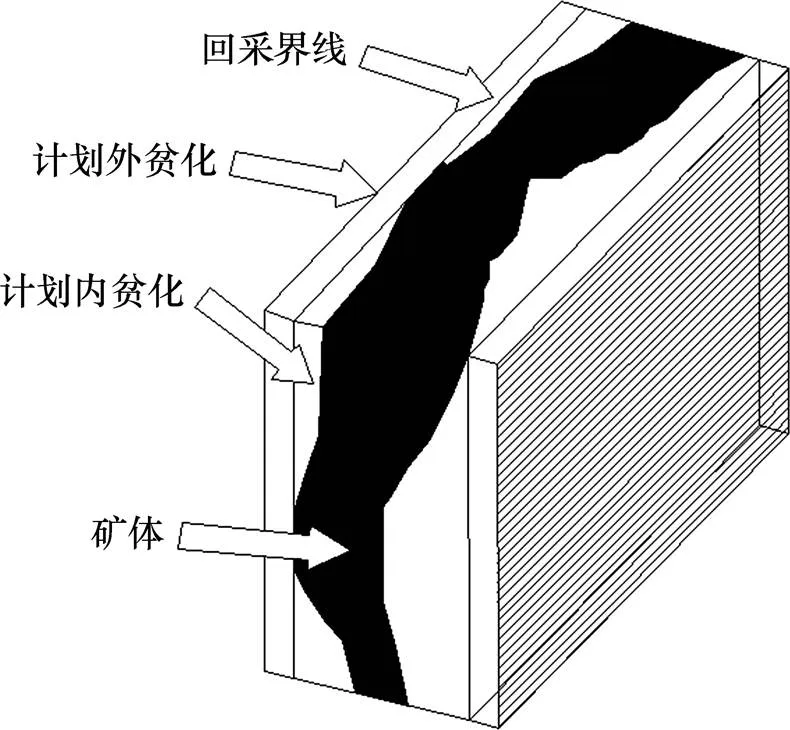
图4 计划内和计划外贫化

依据以往的研究，矿石贫化可以用不同的方式进行定义，例如，长时间对生产进行监测，获得废石和矿石的比例具有重要的意义，然而，这不是评估采场开采是否成功的最优方式，如果只比较废石和矿石的比例，即使是开采非常失败的采场，当坍塌的材料恰好是相邻的采场矿石时，也可以具有较低的贫化率。英属哥伦比亚大学的Brady(1998)引入“等效线性超挖深度()一词来量化贫化的程度[5]，是指从采场边界以外的体积除以相应面的面积(见图5)，这是一个很好的检验采场开采是否成功的方法，因为它不依赖于采场的体积，只与边界的表面积的有关。可以用公式(1)计算，目前，青龙沟采区北矿段处于露天转地下的接替阶段，还没有进行开采，无法现场监测采场上下盘的超挖体积，所以本文采用经验图表和数值

图5 ELOS计算示意图

模拟法来计算值。

3.1 图表法

Mathews稳定图法是由Mathews等人于1980年首先提出的用于1000 m以内硬岩矿山开采设计的方法。其中，Potvin(1988)、Potvin和Milne(1992)、Nickson(1992)通过对加拿大地下矿山350多个案例进行分析，提出一个新的稳定性图表，充分考虑了影响采场稳定的关键因素，稳定性被定性地评估为稳定、潜在的不稳定或塌陷3种情况。估算围岩超挖深度的稳定图表的设计过程是以稳定数′和水力半径这2个因子为基础进行的。

描述采场条件的稳定性系数′定义为[6]：

式中：′为修正后的岩体质量系数；为岩石应力系数，由完整岩石单轴抗压强度c与采场最大主应力1的比值确定，参照文献[7]进行求解；为节理方位修正系数，其值由采场面倾角与主要节理组的倾角之差来度量，参照文献[8]进行求解；为设计采场暴露面的重力调整系数，反映重力对采场岩体稳定性的影响，参照文献[9]进行求解。、、值见表2。

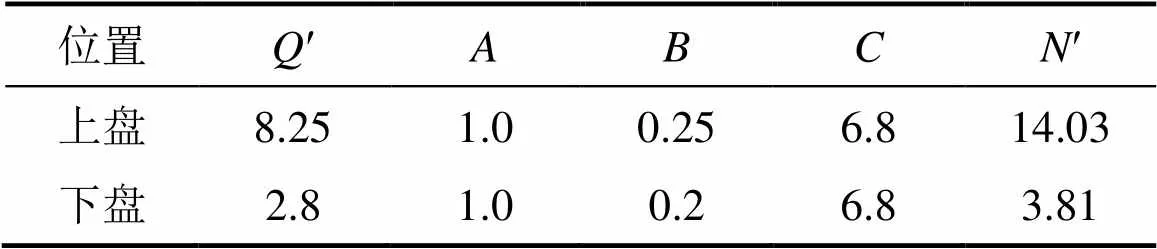
表2 稳定性系数N′计算值

采场的水力半径可以通过下式进行计算：

=/(3)

式中,为待分析采场的帮壁或者采空面的横截面积；为待分析采场帮壁或者采空面的周长。

利用稳定性图对青龙沟采区北矿段采场上下盘超挖深度进行评估，已知采场高20 m，上盘和下盘的稳定性系数′分别为：14.03和3.81，采场长度取12 m、24 m和36 m。分别进行计算(见图6)，计算结果列于表3。上盘超挖深度较小且均小于0.5 m；下盘超挖深度随着采场长度的增加变化为0.7~1.6 m。这说明当采场开挖时，下盘超挖较严重，应对下盘进行支护，防治大量废石混入矿石堆。

3.2 数值模拟法

为了验证上述经验图表法的准确性，运用FLAC3D软件对采场围岩超挖深度进行计算分析。

表3 采场上下盘超挖深度值

(1) 数值模型建立。本文充分考虑3Dmine、MIDAS/GTS和FLAC3D在建模、网格划分和计算分析等方面的优越性，建立了数值计算模型。模型尺寸：X方向长800 m，Y方向长1400 m，Z方向大约高900 m(地表起伏无确定值)，共有228684个节点，1355319个单元体，如图7所示。模型边界采用位移约束，模型四周限制水平方向的位移，模型底边界限制X、Y和Z方向的位移，模型上部边界设置成自由面，采用Mohr-Coulomb破坏准则。

图7 数值计算模型

(2) 数值模拟结果及分析。图8列出采场宽10 m、长12，24 m和36 m时的塑性区云图。采场围岩的塑性区体积通过fish语言编写的显示程序计算出来。利用公式(1)计算围岩超挖深度，结果见表4。

由表4可知，随着采场走向长度的增加采场围岩超挖深度随之增大，其中采场上盘超挖深度增加不明显；图表法和数值模拟法得出的结果具有一致性。

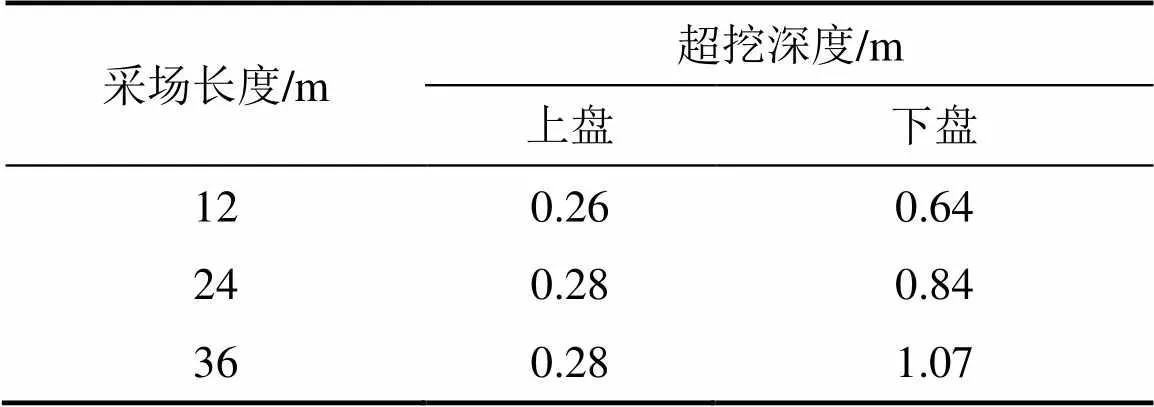
表4 采场围岩超挖深度

4 结 论

本文运用(超挖深度)量化矿石的贫化，通过图表法和数值模拟法对采场矿石贫化进行评估，主要得出以下结论：

(a) 采场长度12 m；(b) 采场长度24 m；(c) 采场长度36 m

(1) 运用Mathews稳定性图表，计算得出上盘超挖深度较小且均小于0.5 m；下盘超挖深度随着采场长度的增加变化为0.7~1.6 m。

(2) 通过数值计算得出，采场上盘超挖深度较小(约0.28 m)且变化不明显，而下盘超挖深度变化较显著，变化范围为0.64~1.07。图表法和数值模拟法得出的结果具有一致性，结果表明：在采场开挖时，下盘超挖较严重，应加强下盘的支护。

[1] 梁德义.矿山经营理念对矿石贫化损失的影响[J].采矿技术,2007(3):170−171+173.

[2] 霍俊发.低品位铁矿床开采降低矿石贫化率的技术措施[J].现代矿业,2013,29(12):87−88+103.

[3] 何 华,江 河.太和钒钛磁铁矿区贫化率和损失率降低措施[J].现代矿业,2016,32(8):39−40+43.

[4] HOEK E, BROWN E T. Practical estimates of rock mass strength[J]. International Journal of Rock Mechanics of Mining Science, 1998, 34(8): 1165−1186.

[5] BRADY T, PAKALNIS R, CLARK L. Design in weak rock masses: Nevada underground mining operations[J]. Transactions- society for Mining Metallurgy and Exploration Incorporated, 2006, 318: 182.

[6] MATHEWS K E, HOEK E, WYLLIE D C, et al. Prediction of stable excavation spans for mining at depths below 1000 m in hard rock[R]. Ottowa: Canada Centre for Mining and Energy Technology, Department of Energy and Resources, 1980.

[7] POTVIN Y. Empirical open stope design in Canada[D]. New York: University of British Columbia, 1988.

[8] STEWART S B V, FORSYTH W W. The Mathew’s method for open stope design[J]. CIM bulletin, 1995, 88(992): 45−53.

[9] MATHEWS K E, HOEK E, WYLLIE D C, et al. Prediction of stable excavation spans for mining at depths below 1000 m in hard rock[R]. Ottowa: Canada Centre for Mining and Energy Technology, Department of Energy and Resources, 1980.

(2018−08−30)

田 军(1962—)，男，辽宁建平人，高级工程师，主要从事岩石力学实验工作。

国家重点研发计划项目(2016YFC0600803)；国家自然科学基金资助项目(51474052)；中央高校基本科研业务费专项资金资助项目(N150102001).