面对称飞行器横侧向稳定控制设计研究

李天任，张 旋，黄 佩，周 华，郝 颖

（中国运载火箭技术研究院研究发展部，北京，100076）

0 引 言

Nonweiler[1]发现的楔形气动构型是最早高升阻比面对称气动构型，随后陆续发展出锥形流[2]、吻切锥[3]等面对称高升阻比构型。在设计飞行条件下，该类构型前缘处产生的附体激波，阻止下表面的高压气体横向“泄露”到上表面，可有效减少飞行器的升力损失[4]，提高其升阻比，进而使其成为高升阻比再入飞行器重要构型之一[4]。面对称高升阻比再入飞行器，气动特性复杂，通道间耦合效应强烈，可能导致控制机构的执行效果与设计预期效果相去甚远。

面对称再入飞行器的气动构型在实际应用中，需设计合适的姿态稳定策略及控制参数，使其能沿着既定的目标飞行。本文采用全状态量反馈控制器，推导出适用于不同状态的控制稳定条件，设计了相应控制策略，并通过不同工况下的参数调整与运动仿真，验证了稳定条件适应性与控制策略有效性。

1 横侧向姿态动力学模型

基于中国航天领域常用的机体坐标系[5]，建立非线性运动学与动力学方程：

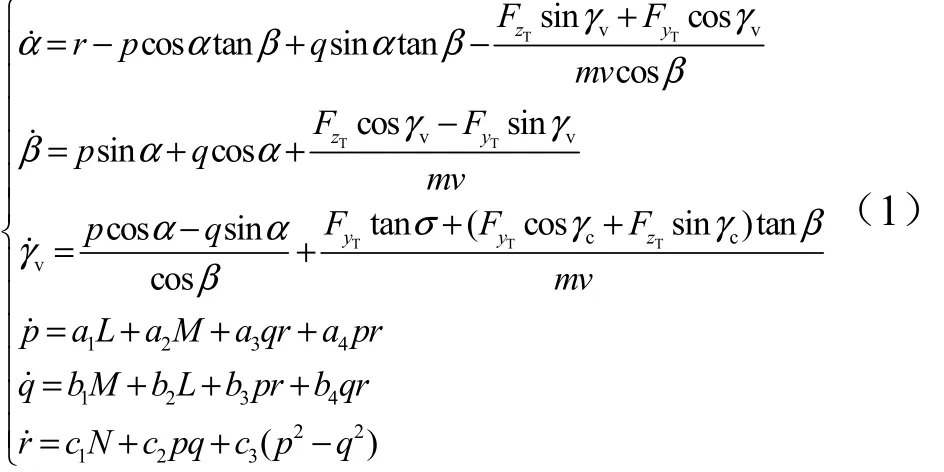
面对称再入飞行器采用倾斜转弯（Bank-to-Turn，BTT）控制方式，侧滑角始终限定在0°附近，忽略纵向运动及气动阻尼项对横侧向运动的影响，并将重力因素划归制导系统补偿，设：δr,δa为飞行器方向舵及副翼舵偏角； Ix,Iy,Ixy为飞行器对体轴 OX，OY的主转动惯量及惯量积； Q , S, lk为飞行动压、飞行器参考面积和参考长度；为滚转力矩系数与偏航力矩系数对侧滑角、方向舵及副翼舵偏角的导数。得到基于平衡状态的横侧向小扰动线性化状态方程为

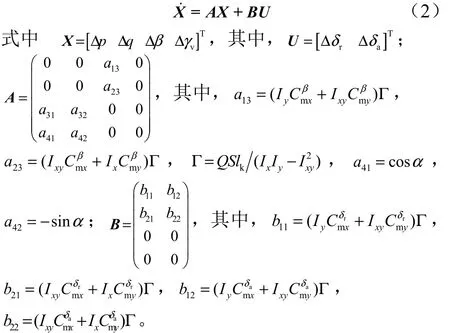
2 控制稳定性分析

2.1 方向舵控制稳定条件

基于式（2），采用全状态量反馈，得到控制器方程为

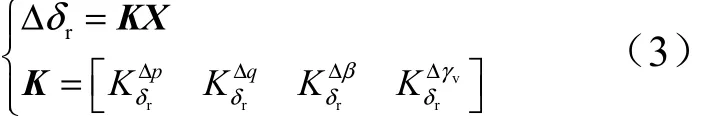
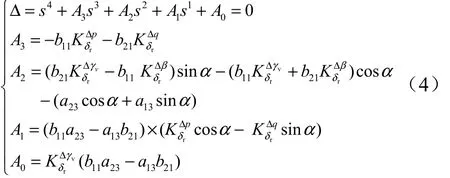
根据劳斯稳定判据，系统稳定的充要条件为

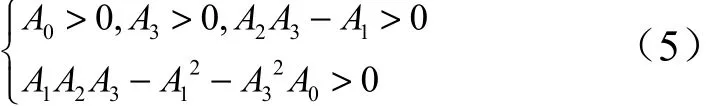
以上充要条件形式复杂，不便于分析，这里推导其必要条件：

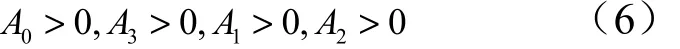
另设：

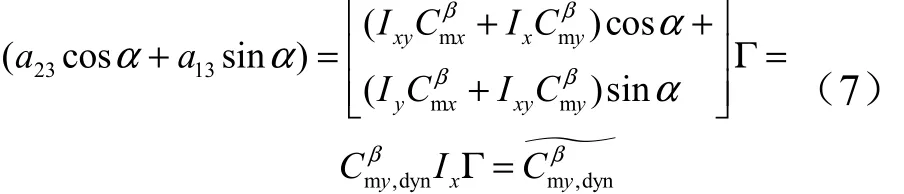
考虑到面对称飞行器通常要求荷兰滚模态稳定，本文坐标系下即有，同时限定飞行攻角在，可得以下稳定条件：

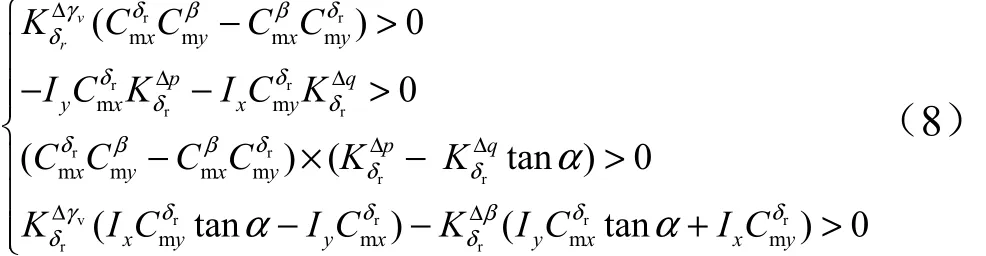
2.2 副翼控制稳定条件

与第2.1节的分析类似，副翼采用全状态量反馈，得到控制器方程如下：

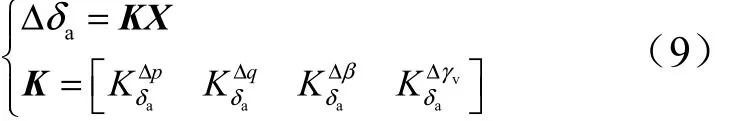
另设：

式中 dLCDP为横向操纵偏离参数（Lateral Control Departure Parameter，LCDP）与 d~LCDP同号。可得以下稳定条件：

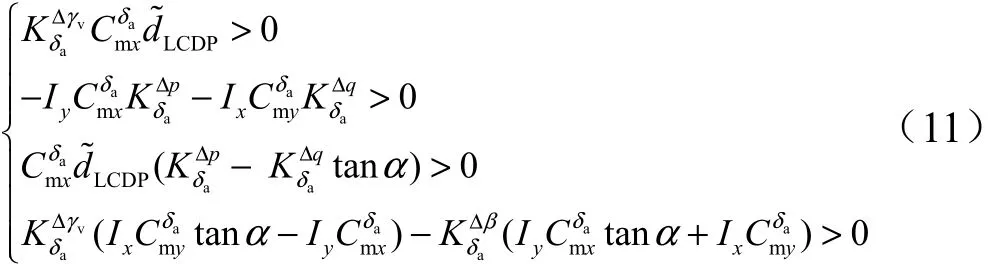
2.3 常规控制稳定条件

根据文献[6]，副翼与方向舵分别控制横向与侧向通道，得到常规控制方程为

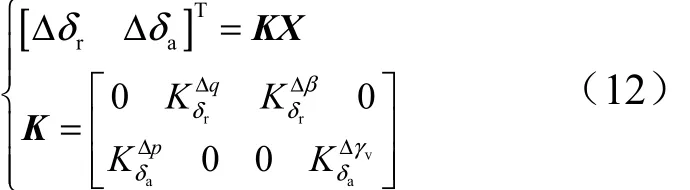
综合式（8）与式（11），得到如下稳定性条件：

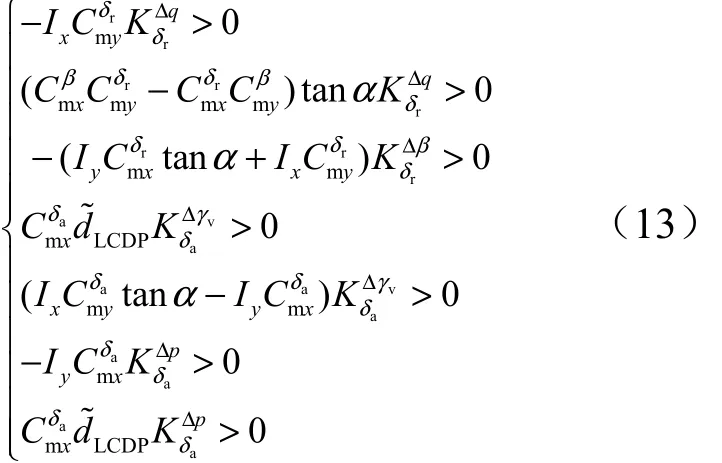
式（13）表明，若飞行器使用常规控制方案实现姿态稳定，则其气动特性需满足：

3 控制器设计与仿真

1958年，Moul和Paulson[7]提出的LCDP判据，是高升阻比再入飞行器气动布局设计与评估的重要指标。因此，本文针对某面对称再入飞行器，分别选取LCDP为负值与正值两个典型飞行工况，进行控制器设计与仿真。

3.1 LCDP小于0

此时，飞行器横侧向状态方程参数取值为：α=10°，a13=-9.57，a23=-0.2885，b11=0.4382，b21=0.1087，b12=-3.294，b22=-0.0642。

这一工况下，按照舵面使用方式不同，设计3类控制策略：

a）策略一：方向舵主导控制横侧向通道，反馈侧滑角、倾侧角及偏航角速度；副翼增稳，反馈滚转角速度。

b）策略二：副翼主导控制横侧向通道，反馈侧滑角、倾侧角及滚转角速度；方向舵增稳，反馈偏航角速度。

c）策略三：方向舵控制侧向通道，反馈侧滑角及偏航角速度；副翼控制横向通道，反馈倾侧角及滚转角速度。

图1展示了输入为1°倾侧角指令时，系统的状态响应及舵偏角曲线。

图1 状态响应及舵偏角曲线( dLCDP＜0)Fig.1 The State Response, Rudder and Aileron Curve (dLCDP＜0)

续图1

由仿真结果可知：

a）副翼主导控制（策略二）与常规控制（策略三）对比：二者在横向通道的表现较为类似，倾侧角、滚转角速度及副翼舵偏角曲线十分靠近，后者的倾侧角跟踪略显快速；在侧向通道上，后者引入侧滑角到方向舵的反馈，因而收敛速度更快。

b）方向舵主导控制（策略一）的机理是先产生负的侧滑角，利用飞行器自身横向静稳定性较大（ Cmβx＜0，a13=-9.57）的特性，进而产生正的滚转力矩，实现倾侧角跟踪阶跃指令。与策略二、三相比：策略一需要较大的侧滑角，另外 Iy与 Ix的比值较大，因此其横侧向通道的收敛速度均慢了不少；阶跃响应初期，倾侧角偏差反馈使得方向舵负偏角较大，而侧滑角尚未大幅增加，正的力矩系数导数（b11=0.4382，0）产生负的滚转力矩，导致倾侧角出现一小段负值。

3.2 LCDP大于0

此时，飞行器横侧向状态方程参数取值为：α=9°，a13=-17.911，a23=-0.185，b11=0.3705，b21=0.09，b12=-8.361，b22=-0.2322。

根据式（8）、（11）及（13）所列的控制稳定性要求，对前文控制策略进行适当修改，得到LCDPd ＞0时的3类控制策略：

a）策略一：方向舵主导控制横侧向通道，反馈侧滑角、倾侧角及滚转角速度；副翼增稳，反馈偏航角速度及滚转角速度。

b）策略二：副翼主导控制横侧向通道，反馈侧滑角、倾侧角及偏航角速度；方向舵增稳，反馈偏航角速度。

c）策略三：方向舵控制侧向通道，反馈侧滑角及偏航角速度；副翼控制横向通道，反馈倾侧角及滚转角速度；采用副翼方向舵交联[8,9]（Aileron Rudder Interconnect，AIR）技术，引入控制器参数KAIR，利用方向舵克服副翼的不利偏航力矩。

图 2为副翼方向舵交联控制结构框图，图 3为dLCDP＞0时的状态响应及舵偏曲线。

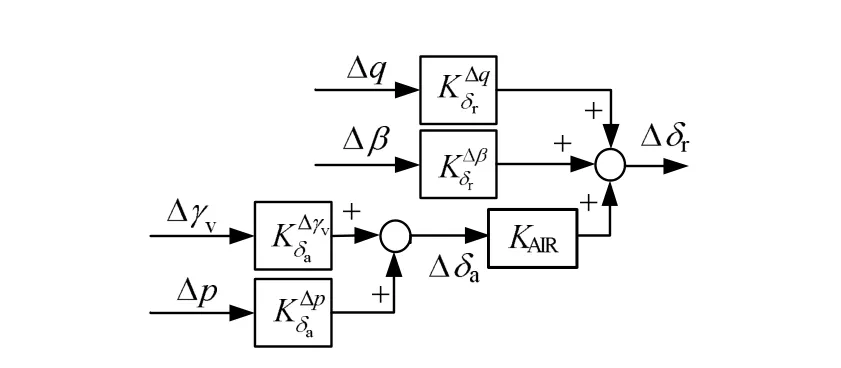
图2 副翼方向舵交联控制结构Fig.2 Structure of Aileron Rudder Interconnect Control

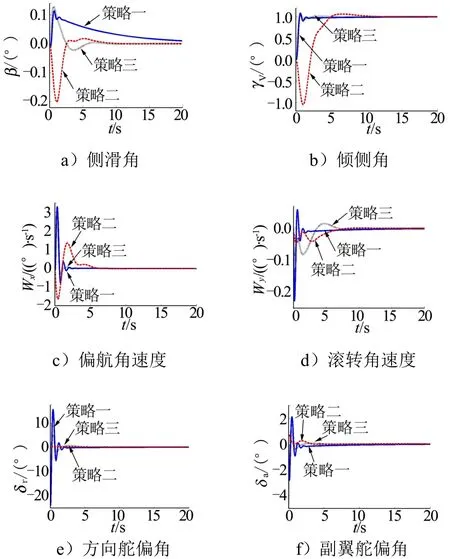
图3 状态响应及舵偏曲线( dLCDP＞0)Fig.3 The State Response, Rudder and Aileron Curve (dLCDP＞0)

由图3所示的仿真结果可知：

a）方向舵主导控制（策略一）与常规+AIR控制（策略三）对比：二者在横向通道的表现较为类似，倾侧角与滚转角速度曲线十分靠近，副翼舵偏角仅在仿真初始时刻（0.1 s以内）偏差较大，随后变化趋势一致；在侧向通道上，前者的方向舵需完成横侧向两通道姿态稳定，因而其舵偏角更大，但侧滑角收敛速度仍慢于后者。

b）对于策略一：虽然其侧滑角始终为正值，且方向舵偏角为负值，横向静稳定性（=-17.911）与力矩系数对方向舵偏角导数（=0.3705）产生的是负滚转力矩，但由于偏航角速度到副翼的反馈（根轨迹如图 4所示）提升了系统稳定性，副翼舵偏角为负值，且力矩系数对副翼舵偏角导数为较大的负值（），使得综合的滚转力矩为正，倾侧角正向增大。策略三的情形与之类似。

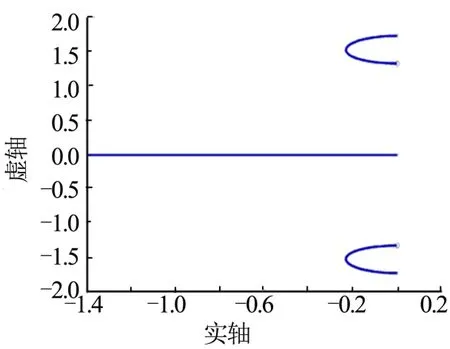
图4 副翼反馈偏航角速度根轨迹Fig.4 Root Locus Diagram for the Feedback from Yaw Angular Velocity to the Aileron

4 结束语

本文以面对称再入飞行器为研究对象，首先从横侧向状态方程出发，基于全状态量反馈，推导了方向舵控制、副翼控制及常规控制的稳定条件。随后，针对LCDPd ＜0与LCDPd ＞0两种工况，各自设计了方向舵主导、副翼主导及常规（+AIR）3类横侧向控制策略。最后，仿真算例显示3类策略均可实现姿态稳定控制，验证了稳定控制条件对不同特性飞行器的有效性与适应性。文中的研究，亦可适用于升力体、融合体、翼身组合体等其它高升阻比面对称构型飞行器，对工程实际应用具有一定参考价值。