应用速燃发动机技术的固体运载器优化设计
2019-07-11黄体圣孙勇强王鹏飞
黄体圣,赵 民,姜 利,孙勇强,王鹏飞
(1. 北京宇航系统工程研究所,北京,100076;2. 中国运载火箭技术研究院,北京,100076)
0 引 言
作为一种重要的航天运载器,多级固体运载器具有响应速度快、机动性强、成本低、可靠性高的特点,目前已成为各国研究的热点[1]。国内外众多研究者对固体运载器的总体参数优化设计方法进行了研究,在研究中一般选取运载能力最优为目标函数[2~4]。但作为复杂的系统工程,在追求运载能力最优的同时,也应兼顾其它性能指标,如效费比、可靠性、生存能力等,而面对日益复杂的应用环境,生存能力的重要性也愈来愈突出。
在固体运载器飞行过程中,一般可分为主动段和被动段(包括飞行中段和再入段),其中主动段发动机红外特征明显,是生存能力较为薄弱的阶段[5]。速燃发动机可显著降低固体运载器主动段高度,被认为是提高主动段生存能力的有效手段[6]。
采用速燃发动机后,一方面固体运载器飞行条件恶化,气动阻力损失大大增加;另一方面发动机流量增大、喷管喉径增加,必然带来发动机质量比的下降,与运载能力最优的目标相矛盾。因此在应用速燃发动机技术的固体运载器方案论证阶段,需对运载能力及生存能力进行综合权衡。多目标优化是解决这类问题的有效手段,可得到所有的非劣解构建非劣解集,而后根据经验从中选取合适的解。
本文针对三级固体运载器,选择主动段高度最小和射程最大为目标函数,应用NSGA-Ⅱ算法完成固体运载器的多目标优化设计研究。
1 系统设计模型
在固体运载器的设计过程中,一般涉及发动机、弹道、气动、姿态控制及载荷计算等多个学科[7,8]。其中发动机是固体运载器最主要的部件之一,决定了固体运载器的构型及性能水平,而弹道设计确定了固体运载器的飞行弹道,是评价其总体性能好坏的核心依据,因此本文选择这两个关键学科构建固体运载器系统设计模型。
1.1 发动机设计模型
由于发动机设计对固体运载器的构型及性能水平具有决定性作用,可选择发动机的设计变量作为固体运载器系统设计模型的输入变量。固体发动机设计变量的选取有多种方式,一般选取一组相互独立的设计变量[9],本文选择的设计变量为:发动机直径mD、装药量pm、工作压强cP、发动机工作时间wt、喷管扩张比ε,其中发动机直径mD根据已有型谱确定,不参与优化。
固体发动机主要由装药、燃烧室壳体、喷管及点火装置等组成,为提高固体运载器性能,本文选用硝酸酯增塑聚醚(Nitrate Ester Plasticized Polyether ,NEPE)推进剂装药、复合材料壳体及喷管。
固体发动机的设计流程较为成熟,主要需对发动机的能量特性、质量及尺寸进行计算。能量特性的关键是对发动机比冲进行预估,其计算公式为

式中 C*为特征速度,可视为常量,由热力计算提供;CF为推力系数;ηcf为比冲效率,可采用回归方程形式的经验公式进行计算[2],即:

式中td为喷管喉部直径,cm;β为喷管扩张半角,(°);AlW为推进剂中铝粉含量的百分比;ε为喷管扩张比。
推力系数FC可由下式计算:

式中 Γ为比热比函数;k为比热比;aP为环境压强;为喷管出口压强。
对于发动机质量计算,为保证计算精度,采用展开型质量模型分别计算燃烧室壳体、绝热层、喷管、前后接头等部件结构质量,质量模型的具体建立过程参见文献[2]。同时,对燃烧室壳体及发动机喷管的尺寸参数进行计算,以获得发动机的整体尺寸。
由设计变量通过发动机设计模型计算可获得各级发动机的性能、质量及尺寸参数。对于方案论证阶段,可认为运载器级间段、电缆网、控制仪器等部件的质量与各级发动机质量成正比,取适当的无因次系数即可获得运载器的各级起飞质量,供弹道设计模型使用。
1.2 弹道设计模型
1.2.1 飞行程序角设计
采用常用的工程设计方法对固体运载器主动段的飞行程序角cxϕ进行设计[10],飞行程序角曲线如图1所示。

图1 主动段飞行程序角曲线Fig.1 Power Flight Programming Angle Curve
具体飞行时序为:点火起飞后,零攻角垂直飞行至t1时刻,t1由运载器推重比确定;此后利用攻角转弯调整推力方向至t2时刻,攻角转弯的最大负攻角为αM,是弹道设计模型的设计变量, t2选择运载器的马赫数为0.7~0.8;而后保持零攻角穿越稠密大气,以减少气动载荷,同时利用重力进行转弯,t3选择为大气稀薄时的高度;最后是定轴飞行段,保持俯仰角不变直至主动段结束。
采用该种程序角设计方法,弹道设计模型只有αM一个变量,由于再入点的当地弹道倾角是影响飞行弹道形态的关键约束,因此,可通过求解方程Θr= Θrmax的方式确定αM,避免了αM参与系统层的优化,提高了系统层的优化效率。
1.2.2 弹道计算模型
考虑地球为标准圆球体,不考虑地球自转,采用标准大气模型,在发射系内建立运载器的三自由度质心运动方程[11],即:
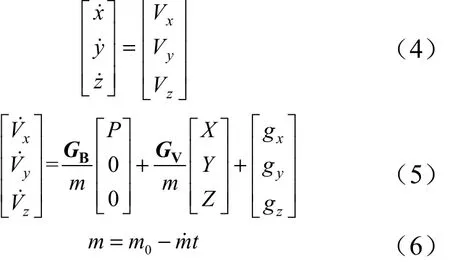
式中 下标x,y,z分别为位置向量在发射系下的分量;Vx, Vy, Vz为速度向量在发射系下的分量; GB为弹体坐标系至发射坐标系的转换矩阵;m为运载器质量;P为发动机推力; GV为速度坐标系至发射坐标系的转换矩阵;X,Y,Z分别为运载器的气动阻力、升力和侧力,本文选择泰坦2火箭的气动力系数进行计算;gx,gy,gz分别为引力加速度在发射系下的分量; m0为运载器起飞质量;m˙为发动机燃气秒流量。
2 优化模型建模
2.1 优化目标
综合考虑固体运载器的运载能力和主动段的生存能力,目标函数选择为:最大化射程L、最小化主动段高度PH。
2.2 约束条件
为限制固体运载器规模,应对固体运载器的起飞质量0m和长度0L进行限制;为限制固体运载器主动段气动载荷及加热量,应对飞行最大动压mq进行限制;考虑到一、二级分离的安全性,应对分离高度sH进行限制;为保证有效载荷中的电子元件正常工作,需对运载器飞行过程中的最大轴向过载xN进行限制。
综合设计变量、优化目标及约束条件,固体运载器系统的优化模型数学表述为

式中 下标:j为发动机级数,lim为各约束的限定值;X为设计变量; XL, XU分别为设计变量的取值下限和上限。
2.3 优化算法
对于求解多目标优化问题,主要有归一化算法和非归一化算法两大类[12]。归一化算法是采用加权法、约束法和目标规划法等手段将多个目标转化为单一目标,但为了获得Pareto最优解集,必须运行多次优化过程,求解效率低。非归一化算法是采用Pareto机制直接处理多个目标的优化技术,不需要将多个目标转换为单一目标,并且能够使所求解集尽量均匀覆盖Pareto前沿,避免了归一化算法的缺陷,在多目标优化问题中得到广泛的应用。
在移动互联网时代高速发展的今天,中国铁路沈阳局集团有限公司如何利用互联网+的思维模式实现管理转型与创新,特别是对集团公司内部的审批业务模式的改革与升级势在必行。
非支配排序遗传算法(NSGA-Ⅱ)是最具代表性的非归一化算法,该算法是在传统遗传算法的基础上发展而来的,其基本思想是首先对父代种群进行遗传操作,得到子种群,再将父代和子代种群合并,而后进行非支配排序和拥挤距离排序,得到新的种群,反复进行直到算法设置的最大迭代次数[13,14]。NSGA-Ⅱ算法具有优秀的探索能力,在多目标优化问题中得到广泛应用,本文也采用该算法进行求解。算法参数设置为:种群规模100,进化代数100,交叉概率0.9,交叉分配指数20,变异分配指数100。
本文构建的优化模型如图2所示,实现方法为采用 C++语言编制发动机及弹道设计模型,通过优化软件Isight进行集成优化。

图2 固体运载器多目标优化模型示意Fig.2 Multi-objective Optimization Model of Solid Launch Vehicle
3 仿真分析
3.1 仿真条件
某固体运载器的总体任务需求及约束条件为:有效载荷1.5 t,起飞质量0m不大于50 t,长度0L不大于18 m,飞行最大动压mq不大于150 kPa,分离高度sH不低于20 km,最大轴向过载xN不大于40g。在实例优化仿真中,设计变量的优化区间如表1所示。
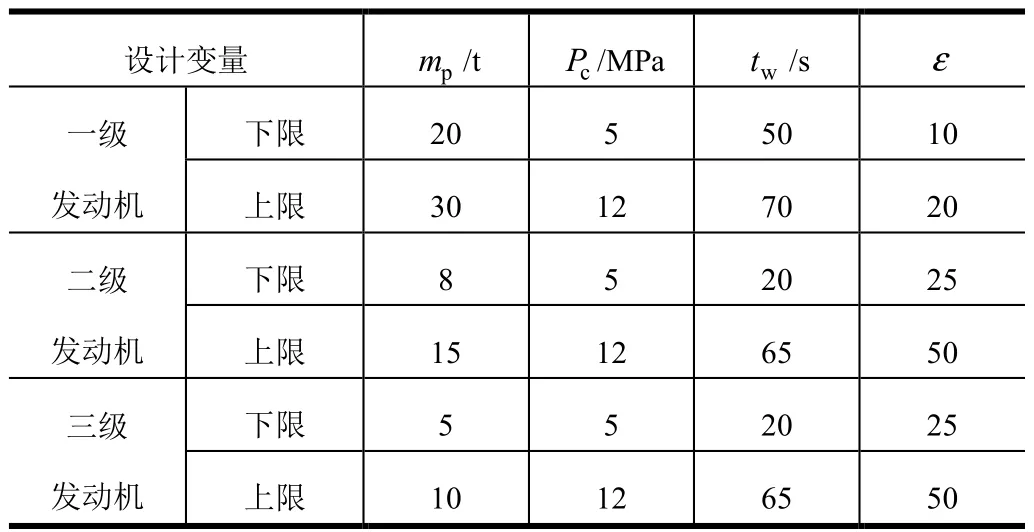
表1 设计变量的优化区间Tab.1 Optimal Interval of Design Variables
3.2 优化结果及分析
采用本文所构建的固体运载器系统优化模型进行仿真分析,获得的Pareto前沿如图3所示。

图3 Pareto前沿Fig.3 Pareto Frontier
由图3可知,采用NSGA-Ⅱ算法优化得到的Pareto前沿分布较为均匀,且散布范围广,可满足固体运载器系统优化设计的要求。此外,图3表明主动段高度越低,射程损失增加的越快,当主动段高度低于80 km时,射程损失急剧增加,因此在方案综合决策时,主动段高度不宜过低。
表2和表3给出了Pareto解集中的具有代表性的解及其相应的性能参数,表3中1r,2r和3r表示各级发动机燃速。图4和图5给出了这3个解的主要弹道特征曲线。
由表2和表3可知:
a)相比于正常燃速的方案3,方案1的射程损失约1800 km,但主动段结束高度为75 km,是方案3的一半,这对运载器主动段生存能力的提高大有好处;
c)为降低主动段高度,一级发动机燃速变化不大,主要需增大二、三级发动机燃速,方案1的燃速需增加至方案3中正常燃速的2.5倍左右,可通过添加燃速调节剂实现,美国在实际工程中应用的NEPE推进剂燃速可达30 mm/s[6],达到表中各方案所需燃速,可以实现75~100 km大气层内关机是可行的。

表2 固体运载器部分设计结果Tab.2 Partial Design Results of SLV

表3 固体运载器部分设计结果的性能参数Tab.3 Performance Parameters for Partial Design Results of SLV

图4 主动段高度随时间变化曲线Fig.4 Curve of Height for Power Flight
4 结 论
采用NSGA-Ⅱ算法开展多目标优化分析,得到如下结论:
a)针对固体运载器多目标优化问题,可采用NSGA-Ⅱ算法仅通过一次优化仿真获得分布均匀、散布范围广的Pareto解集,方便进行综合决策;
b)对于不同主动段高度的设计方案,二、三级发动机设计参数变化较大,主要体现在随着主动段高度的下降,工作时间缩短及燃烧室压力升高;
c)当固体运载器主动段高度低于80 km时,运载能力损失急剧增加,在方案综合决策时,不宜选择过低的主动段高度。
