长江经济带新能源汽车零部件库存与运输整合优化研究

摘 要：新能源汽车因其运输路线规划的不合理，总成本居高不下。本文选取长江经济带的重要节点配送中心为实例，对新能源汽车零部件物流系统进行调查研究，构建多元线性回归模型，分析运输距离、运输量、周转次数与总成本的关系，通过对三项指标的合理设计，得出总成本可降低的具体数值，分别为31.95112元/km、17.75872元/百件、129.6443元/次，三者影响大小以周转次数、运输距离、运输量排列。以此为基础构建降低物流成本的最优配送方案，从而达到降低成本的总目的。

关键词：长江经济带;新能源汽车;库存—运输整合优化

中图分类号：F253文献标识码：A文章编号：1008-4428（2019）04-0022-02

一、 引言

长江经济带因有着丰富的自然资源、人才资源，其市场广阔、交通便捷、产业众多，因此人口和生产总值均超过全国的40%，有着巨大的发展潜力，是中国重要的经济发展领域之一。近年来为优化产业结构以获更大的发展，长江经济带集中发展新能源产业，其中新能源汽车更是重中之重。然而，作为整车行业的基础，汽车零部件行业因仓库容量有限，零件数量繁多，配送计划不合理等诸多因素，导致物流系统总费用高昂。制定配送计划时如何整合优化库存控制与路径规划，降低物流成本，成为亟待解决的关键问题。

在经济全球化的背景下，供应链一体化的趋势愈发显著，由于库存与运输之间存在着“效益背反（trade-off）”的关系，决定了对其进行综合研究分析，有利于从整体上提高物流效率、降低物流成本，两者的联合优化也成为研究热点，Chuah和Yingling基于库存与运输的关系，建立循环模式的数学模型;Nagesh Shukla等三人构建了随机性需求下的单供应商和单零售商的库存运输模型;Chen和Sarker建立了多供应商、单一制造商的循环取货集成优化模型。国内也有许多相关研究，施朝春等构建了Milk—Run模式的双层规划模型;赵达等对直接配送策略下随机需求库存—路径问题进行研究;杨志林等在随机需求且允许缺货的条件下构建了单个供应商—多个零售商的生产—库存—运输的整合优化模型。

以上库存与运输联合优化研究侧重于通用理论模型与算法研究，注重物流供应运作模式的研究，对长江经济带的汽车零部件物流系统优化没有进行针对性的研究，长江经济带覆盖面广，各个地域对新能源汽车的支持政策均有所不同，且零部件技术要求高，零件数量繁多，具有特殊性。本文以上海汽车售后配送中心、武汉上汽通用汽车配件配送中心、襄阳长英物流分公司、重庆聪聪·高新物流配送中心等新能源汽车零部件配送中心为核心，构建多元线性回归模型并设计求解，根据模型分析得出影响总成本的显著因素，以便构建降低物流成本的最优配送方案，从而达到降低成本的总目的。

二、 现状

（一）长江经济带

长江是中国最长、流域最广的河流，长江经济带依长江而生，横跨我国中东西三大区域，覆盖11个省市，有着巨大的发展潜力。近年来，国务院接连印发《关于依托黄金水道推动长江经济带发展的指导意见》《长江经济带综合立体交通走廊规划（2014—2020年）》《长江经济带发展规划纲要》，体现了国家对长江经济带发展的高度重视。

长江经济带宏观经济发展近几年来一直稳中有进，然而绿色发展指数与创新发展指数却增速缓慢。2011—2017年长江经济带绿色发展指数中，前三年发展迅速由49.39增长到54.9，之后四年发展速度放缓，然而一直在稳步提升。另一方面，长江经济带的创新驱动力在2011—2013年间，由41.63上升到53.37，而在2014、2015又下降回43.17，年增速仅为0.72%。作为创新绿色发展领域中的佼佼者，新能源汽车理应受到重视、改进和发展自身，从而为GDP的发展做出更大的贡献。

（二）新能源汽车

从2001年起新能源汽车研究项目被列入国家重大科技课题，2008年开始，新能源汽车的话题在我国受到的关注度不断提高，至今仍有极高的热度。新能源汽车拥有政府支持补贴、自身节能环保以及噪声小等诸多优点，也存在着续航能力差、充电难等缺点。但不可否认在国家的大力推行下，傳统汽车终将退出市场被新能源汽车取而代之。

新能源汽车的产量月均8万辆以上，且有着不断上升的趋势。据推测，中国的汽车需求仍在不断增加，到2020年，中国的汽车市场将达到2000亿元，对新能源汽车的产业要求也在不断提高，因此即使是占有优势的新能源汽车若不进一步发展完善自身，提高企业竞争力，也一定会在激烈的市场竞争中落败。

新能源汽车作为中国七大战略性新兴产业之一，被国家密切关注且支持，然而中国的新能源汽车产业仍存在关键核心技术未能完全掌握和民族品牌缺乏的问题，长江经济带覆盖面广，上、中、下游地区各有其独特的优势，武汉、襄阳、福田、长沙等众多位于长江经济带的城市都竞相发展新能源汽车产业，为了降低成本，以提高企业竞争力，新能源汽车零部件物流的整合优化研究必不可少。

（三）汽车零部件物流

在汽车制造业中，零部件制造业可谓是至关重要的一部分。在汽车工业的成本中，汽车零部件制造业占了绝大部分，随着时间的推移比重逐步上升，到了2017年，它在汽车工业的制造成本中甚至高达70%。而物流却在零部件制造业中占了近14%。因此若能有效地降低物流成本，也能有效地降低总成本，进一步达到提高利润、增强企业竞争力的效果。

三、 问题描述及模型构建

物流成本是一座冰山，其沉在水面下的黑色区域还有很大的开发潜力。运输及库存是物流中最具潜力的利润创造源，而它们之间还存在着“效益背反”的关系，需要进行合理的整合优化，以求最大化的降低物流成本，达到价值的最大化。

新能源汽车零部件运输与库存的综合优化就是汽车生产商在目前所采用的JIT生产模式，以及对零部件供应的硬性需求和各种客观因素的限制下，追求最优的运输与库存解决方案，使整个供应物流系统运输与库存的总费用达到最小，从而显著降低成本，有效提升企业效益，改善企业运营效率。

在实际问题中，影响汽车零部件库存—运输成本的因素太过繁多和琐碎，本文由于数据来源、简化计算等诸多考虑，仅选择距离、运输数量和周转次数这三个最为显著的因素作为自变量进行研究。根据多元回归模型建立以下方程：

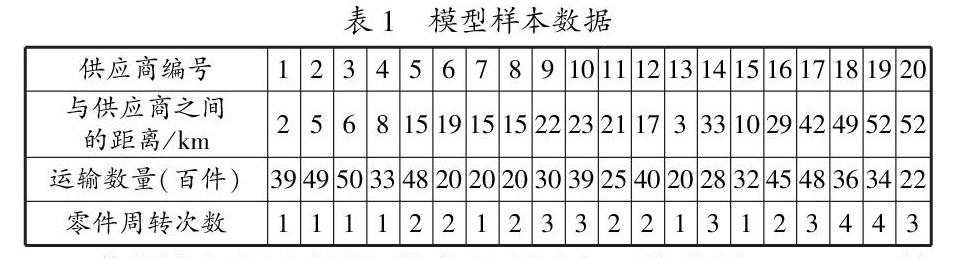
襄阳是长江中游城市群重要成员，也是湖北省省域副中心城市，近年来襄阳积极响应国家号召，保护环境绿色发展，着重发展新能源汽车产业且成果显著。通过对上海汽车售后配送中心、武汉上汽通用汽车配件配送中心、襄阳长英物流分公司、重庆聪聪·高新物流配送中心的走访调查，对他们企业每天的大致運输量，与运输工厂的距离，大致运营成本等数据，并对运输过程、企业内部组织进行了观察，之后通过spss软件进行整理录入，表1为整理出的部分数据。

依据市场调查结果，设定短程固定运输费用C0=200（单位：RMB），针对本案例所处的宏观条件和自然条件限制，做出如下设定：

1. 在运输过程中发生的特殊情况不计入在内，如发生交通事故等。

2. 忽略在中转过程中由于不同汽车生产商所规定的特殊要求而产生的额外费用。

3. 由于不同的供应商所负担的责任和职责可能不同，例如有些生产商只要求供应商将零部件整包配送至储存地，而有些生产商则要求直接配送至车间。在本案例中，忽略这种情况所产生的运输成本。

四、 模型回归分析

（一）模型回归结果检验

在多元回归模型中，t值是一个重要的判断标准，如果得到的t值超过临界值就代表该自变量对因变量影响显著。查表可得本文t值的临界值为2.101。

F检验是多元线性回归模型中的另一重要检验，是用于检验总体回归方程的显著性。查表可得，本文F检验的临界值为2.46。

在回归分析中，p值用来检验系数的显著性水平，值越小表示变量越显著，超过0.05则判定系数不显著。Prob.是检验F检验本身的显著性，判断方法与P值一致。

R2度量了Y与所有解释变量的线性相关程度，计算方法为R2=ESS/TSS，其中ESS代表回归平方和，TSS代表因变量Y的总平方和，越接近于1越能说明模型的准确性。

VIF（方差膨胀因子）是判断模型是否存在多重共线性的重要标准。VIF越大，显示共线性越严重，反之存在的可能性越小。一般以10作为共线性存在与否的分界线，超过10说明存在多重共线，反之不存在。

（二）模型回归结果

由表2可得：本模型设定显著水平α=0.05，查表得到对应的t值的临界值为2.101。得到的结果中X1、X2、X3的t值分别6.228911、4.865588、2.631514均大于临界值，P值为0.0000、0.0002、0.0223均小于0.05，即三个变量均通过显著性检验，说明选取的三个自变量对因变量影响显著。

在回归结果中F=94.7，且Prob.=0.0000<0.5，说明模型通过F检验，拒绝0假设，即表示解释变量Y与被解释变量X1、X2、X3之间有明显的线性关系。

该模型的拟合优度R2=0.94，调整后的拟合优度R2=0.93，均大于0.9且接近于1，所以该模型的拟合程度很高，模型准确。

表2中的模型结果显示的VIF均小于10，说明解释变量之间不存在多重共线性。

最终根据模型结果建立多元回归方程：

从模型结果来看，不难发现，运输距离X1、运输数量X2、周转次数X3均对成本有正向影响，即距离越大，运量越大，周转次数越多，总成本越大，且三者影响大小以周转次数、运输距离、运输量排列。

五、 结语

新能源汽车是集创新和环保于一体的新兴产业，引起社会的诸多热议，作为其根基的零部件物流也成为企业重点关注的对象。本文分析了新能源汽车零部件物流的现状以及发展的必然性。并对新能源汽车零部件的运输过程进行回归分析，分析运输距离、运输数量、周转次数与总成本之间的关系。以长江经济带四个主要城市的汽车零部件配送中心作为研究对象，收集数据建立多元回归线性模型，发现距离越大，运量越大、周转次数越多，总成本越大，而且三者影响大小以周转次数、运输距离、运输量排列。

本文中构建的模型相对简单，但这也说明在库存—运输这一整体中仍存在着诸多成本浪费现象以及值得挖掘的利润，还有优化上升的空间。这对降低物流总成本、提高企业竞争力有着积极的推动作用。

参考文献：

[1]Chuah K H Yingling J C.Analyzing Inventory/Transportation Cost Tradeoffs for Milkrun Parts Delivery Systems to Large JIT Assembly Plants[C].AerospaceManufacturing Technology Conference & Exposition，2001.

[2]Nagesh Shukla，M.K.Tiwari，Darek Ceglarek.Genetic-algorithms-based algorithmportfolio for inventory routing problem with stochastic demand[J].nternational Journal of Production Research，2013，51（1）：118-137.

[3]Chen Z，Sarker B R.An integrated optimal inventory lot-sizing and vehicle-routing modelfor a multi-supplier single-assembler system with JIT delivery[J].International Journalof Production Research，2014，52（17）：5086-5114.

[4]王旭，施朝春，葛显龙.基于Milk Run模式的库存运输整合优化[J].计算机集成制造系统，2011，17（4）：852-857.

[5]赵达，李军，马丹祥，李妍峰.直接配送下随机需求库存-路径问题最优平稳策略及其算法[J].中国管理科学，2014，22（6）：61-68.

[6]杨志林，李擎卿，林冠男.随机需求下单供应商与多零售商的生产—库存—运输联优化模型[J].大学数学，2015，31（5）：12-19.

[7]叶志坚，杜文，王清荣，朱健梅.供应商管理库存系统中库存和运输计划整合[J].交通运输系统工程与信息，2003（4）：82-88.

[8]肖继先，康玉茜，孔闪闪.最大最小运送周期下的库存与运输优化模型[J].辽宁工程技术大学学报（自然科学版），2013，32（3）：393-396.

[9]葛显龙，辜羽洁，王伟鑫.供应链环境下的库存与运输整合优化模型及算法[J].系统工程，2014，32（1）：26-32.

[10]汪金莲，蒋祖华.汽车制造厂零部件入厂物流的循环取货路径规划[J].上海交通大学学报，2009，43（11）：1703-1708，1714.

[11]叶志坚，杜文，王清荣，朱健梅.供应商管理库存系统中库存和运输计划整合[J].交通运输系统工程与信息，2003（4）：82-88.

作者简介：

江铭佳， 女，湖北武汉人，湖北文理学院管理学院学生，研究方向：事物流管理。