小学数学教学等量代换思想渗透例谈

吴彩凤

“等量代换”是指用一个量取代与之相等的量。应用在数学中，其实质便是用已知的量代换未知的量，或按照已知的关系，代换推导出新的关系，使复杂题目简单化，抽象题目具体化，从而达到解决问题的目标。等量代换是数学中一种基本的思想方法，也是代数思想方法的基础。这个数学思想方法在数学学习、研究中有着广泛的应用，它贯穿于数学学习的各个阶段，尤其是到了中学，使用更为广泛、频繁，如解多元方程、几何推理、函数等。因此，在小学阶段的数学学习中，渗入并训练等量代换思想方法对学生今后的数学学习无疑是具有积极意义的。那么，如何在小学数学教学中渗透等量代换思想呢？

一、通过对题目的选择与分析，渗透数学代换的“生活性”

小学数学课堂倡导“从生活中来，到生活中去”，等量代换思想在日常生活中更是常见，对此，教师在宏观把握教学内容和熟练运用教学方法的基础上，可以进一步分析与选择更接近学生生活的例子，设置生活问题情境，引导学生结合生活实际思考问题，有利于学生对知识的理解与掌握，体会数学与生活的联系。比如北师大版一年级上册的第二单元《比较》中，就有等量代换思想的渗透。

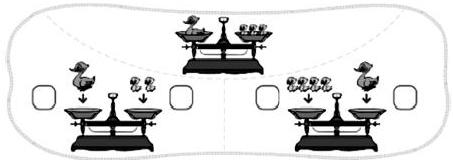
对于小学一年级的学生而言，等量代换思想方法是抽象的，而教师根据课本内容，巧妙的利用学生喜欢且好奇的“小鸡小鸭”作为教学例子，激发了学生的学习兴趣，其中呈现1只小鸭重量=3只小鸡重量，用3只小鸡代换一只小鸭，则3只小鸡比2只小鸡重，4只小鸡比3只小鸡重的代换比较过程，突出了等量代换教学中浓浓的“生活味”。

创设学生日常生活可能遇到情景，可以促使学生理解问题，对学习产生兴趣;同時这有利于培养学生用数学思考问题的意识，联系生活解决实际问题习惯，以及善于发现生活中数学的美的能力。

二、通过要素提取与概括，渗透数学代换的“程序性”

在理解的基础上，教师可以引导学生从题目中提取等量代换的要素，一是指被代换的对象，二是指用来代换的对象。被代换对象通常是问题语境里的直观量，这个量是未知的，需要通过与它相等的另一个量或式子代换后才能最终解决问题。代换对象，即与被代换对象相等的量或式子。另外，在提取要素后，为了理清解题思路，明确解决方案，可以引导学生分析文本，概括关键信息，呈现与原题文本形式有别的数字化的关系式。通过提取要素以及概括关键信息的过程，使学生体会数学语言表达的简洁美，以简代繁，更直观地看出要素之间的数量关系，有效突破思维的转换局限。

比如，执教《用方程解决问题》（北师大版小学五年级下册第七单元）中的“相遇问题”时，没有采用“让学生理解从两地相向同时出发行走，直至相遇的直观情境画线段图表示列方程解决问题”这一常规方法，而是聚焦于等式“淘气走的路程+笑笑走的路程=总路程”“淘气行走速度×时间+笑笑行走速度×时间=总路程”“70x+50x=840”，这个逐步代换的过程能充分体现学生数学思维的层次性。这个代换、推导的过程，恰恰是培养学生数学精神、数学思想方法的重要环节。以下是具体实施步骤：

1.认真分析题目，根据问题情境列出直观的等量关系

（1）结合图示，仔细读题，说说题目的意思。

让学生说出题目的已知信息：总路程、总路程由两个人共同走完、两个人的行走速度、求需要的时间。

（2）这一段路程，由两个人朝不同方向共同走完，你能理解这个意思并列出等量关系式吗？

由两个人共同走完一段路的问题是学生第一次遇到，这是一个比较复杂的问题，综合性比较强，学生不容易一步到位。但根据题目的表述，可以先提取“淘气走的路程”“笑笑走的路程”这两个要素，列出直观的“淘气走的路程+笑笑走的路程=总路程”这一等量关系式，则在学生理解能力范围内。

2.寻找能代换未知量的式子，列出新的等量关系

（1）淘气和笑笑走的路程都不知道，不能直接列出方程，你能用之前学过的知识，找到别的式子来代换吗？

这个问题让学生首先独立思考，然后交流讨论，最后商定答案。通过课前复习路程问题的公式，学生可以得出答案，即“速度×时间=路程”。

（2）学生列出代换后的等量关系式。这一部分交给学生相互探讨完成，即列出：淘气行走速度×时间+笑笑行走速度×时间=总路程。

寻找用来代换的对象，并代入原等式，是一个难度较大的环节，但学生初步掌握了路程问题的基本计算公式，且初步接触过等量代换的思想，解决“代换后的等量关系式”等问题的难度不大。尽管如此，让学生充分思考、交流、探讨，还是很有必要的，这有助于学生解题思路的形成。

3.用数字符号代换文字，列出简便的数学等式

淘气和笑笑的行走速度已经知道，这个环节的关键是让学生明白，淘气和笑笑的行走时间是相同的，也是题目要求的，设为x。这样，代入已知量和未知数的等式为：70x+50x=840。最后，由学生解方程，得出答案。

通过以上“变异”代换的方法，使复杂的式子简单化，拓宽解题思路;建构小学生可理解的、可掌握、可应用的等差数列求和公式，开阔学生的数学视野。总之，将原题进行结构上的变异或者方法上的求异，使思维拓展落到实处，对学生的思维发展以及数学眼光的开阔具有一定的意义。

整体而言，渗透有“生活味”的等量代换重在“激趣导入”，多用于“初步感知”和“联系生活”环节，意在为进一步形成抽象的基本代换思维步骤奠定基础;渗透等量代换的“程序味”重在“形成思路”，多用于“自主探究”“总结归纳”等环节，意在使学生思维经历“具体—半抽象—抽象”的全过程，有感知内化的意味;渗透等量代换的“变异味”重在“思维拓展”，多用于“拓展提升”等课余兴趣环节，意在开拓学生的发散思维。

根据学生的需要和认知情况，教师通过对题目的选择、提炼、概括、拆分、转换等方法，渗透代换的“生活味”“程序味”“变异味”，不失为培养学生等量代换思想方法的一种新途径。【基金项目：岭南师范学院教育教学改革项目“区域教学模式本土化的变革实践”（项目编号：LSJGZB1810）】

责任编辑 黄日暖