自然灾害区域疏散的预警优化模型研究
2019-07-10苏子逢
孙 典, 宋 艳, 苏子逢
(1.清华大学 公共管理学院 应急管理研究基地,北京 100084; 2.上海外国语大学 国际工商管理学院,上海 201620; 3.北京大学 博士后流动站,北京 100871; 4.国家开发银行 博士后科研工作站,北京 100032)
0 引言
近年来自然灾害事件频发,如台风洪水等灾害给人们生命财产安全带来了极大的伤害。而在类似的灾害情况下,可以通过有预警的应急疏散规划,对危险地区的人群进行有计划的疏散,进而减少人员伤亡。应急疏散作为应急管理中的主要功能模块,其情景可分为灾害到达时间基本确定和到达时间不确定两类。前者如台风,洪水,泄漏毒气等可以通过气象手段判断短期时空轨迹[1],针对此类问题,管理者需要考虑在限定时间内,高效地将民众疏散至安全区域。
针对大规模的区域疏散问题,国外的研究较为丰富,Murray-Tuite和Wolshon回顾了近十年来疏散模型和仿真,并指出明确和有效的疏散指令沟通是实施疏散的关键[2]。Lindell和Hwang强调了考虑预警信息特定的接收者和沟通媒介的重要性[3]。大量研究表明关于灾害条件的信息会帮助人们进行决策[4],而预警信息可以从国家气象服务部门,媒体,同级(朋友,亲戚,邻居,同事)和政府官方获得。然而,不是每个信息来源都有相同的可信度,当人们从不同的渠道获取信息时会导致疏散指令的不同服从度[5],而疏散者是以从不同渠道获得的信息为依据来进行疏散[6]。Burnside在疏散行为的研究中强调了多重信息来源的重要性,当多重信息都共同确认了相同的疏散预警信息,会诱使个体进行疏散[7]。
Fu和Wilmot利用离散选择理论建立了有序的logit模型用来预测将采取疏散行动的人群比例,把与时间有关的因素和被疏散者在不同时段的选择联系起来[8,9]。Chen和Zhang假设每个人都会接到疏散指令且当接到指令后才会进行疏散,编码并列举备选的按照区域有序进行疏散的方案,是探索分阶段疏散问题的早期研究[10]。Lim 等人为以台风为代表的短时间疏散预案提出了一个限量的网络流量模型来最大化被疏散人群的总人数。这种方法建立在时间拓展网络基础上,发展了一个用来处理疏散路线,流量,时间表的分配的决策工具[11]。Swamy等人则为公共交通疏散提出了一个多阶段的方法,形成了一个预案的研究框架,包括定位危险区域,分配避难点,设计疏散路径,运用仿真建模的方法为公共交通疏散提供科学决策依据[12]。
国内关于大规模应急疏散的研究较少,很多学者从公共交通入手对集结点选址和公交车辆行驶路径规划问题展开研究[13],提出基于公共交通的疏散组织方案和疏散策略[14]。从私家车疏散入手的研究在国内并不丰富,有从涉及信息方面着手分析路径选择,目的地选择等优化问题,从而减少疏散过程中的交通阻塞[15~18]。在研究应急管理中的路径问题时,代颖等人将物资需求信息和路网信息的动态变化转化成了离散点的静态决策问题[19]。俞武杨设计了一种嵌入迭代线性规划的启发式模拟退火算法对应急物资的运输的非线性模型进行求解[20]。
综上所述,疏散行为的执行者和管理者是疏散问题的关键,一方面管理者发布疏散预警信息,另一方面执行者自行决定是否疏散以及疏散的时间。为了整体的疏散效率最大化,政府在进行疏散时通常以全局的角度进行规划,并适时地发布疏散指令,目的是避免被疏散个体因无序逃离而造成的拥堵滞留现象,这种现象会导致灾害风险的增加。因此,疏散指令发布的时间,方式以及内容尤其重要,直接影响被疏散者决定撤离的时间和数量。此外,在疏散的过程中,被疏散者对于疏散指令的响应也决定了在不同时段的交通需求。很多研究调查了疏散预警来源的利用和它潜在的对于台风疏散行为的影响[6~8],但关注于优化预警发布方式以提高疏散效率的研究基本没有。我国现有的区域应急疏散研究较少,多从交通网络出发采用仿真的方法[21~23]主要涉及路径和选址等相关问题[24~27],大规模区域疏散及其风险沟通的研究相对较少,而与之对应的对信息发布机制与疏散效率关系的研究更是匮乏。
本研究适用于自然灾害如洪水台风等有预警灾害的大规模区域疏散,主要针对私家车疏散群体,包括两个模型,决策的变量包括1)分配交通路径(为每个预警地区分配避难点);2)影响需求的预警发布决策。这种方法考虑如何发布信息以驱动疏散过程,将人的行为因素与交通系统相结合,其中预警发布问题的数学模型,考虑了时间维度,区域差别以及发布渠道的不同影响效果,将在一定时间内最大化疏散人群数量为目标,优化信息发布的策略,减少道路中的堵塞,为制定应急疏散预案提供科学依据。针对模型的特点设计了贪婪的迭代启发式算法,最后给出算例,结果表明了模型和算法的有效性和可行性。
1 模型研究
1.1 问题描述
对于到达时间基本确定的自然灾害,需要启动应急预案对危险区域的公众进行疏散。通常政府会指定一些安全地区并配备相应公共设施的避难点,并为危险地区的公众发布疏散预警信息,包括灾害严重性,疏散指令以及疏散路径等,最大程度的保证公众的人身及财产安全。在疏散过程中需要解决的首要问题是减少疏散过程中的混乱,准确高效及时地疏散危险地区的人群。本研究旨在优化疏散预警消息发布的不同渠道及时间,在自然灾害来临之前更好的将消息传递给特定地区的人群,以期减少道路阻塞,提高应急疏散效率。研究框架主要包括以下几个步骤:
首先,确认危险地区:根据灾害的严重性确认需要被疏散的危险区域,并根据人口普查的区域边界划分,把危险地区划分成不同的地理区域,这样可以保证获取人口信息。被疏散地区的点的定位是根据地理区域的面积大小和位置利用区域的重心来标记的。
第二,确认疏散路径:在定位被疏散的区域点和避难点后,需要确认被疏散者可能采用的疏散路径,假设所有自行疏散的群体都利用最短路径来进行疏散。本研究利用Dijkstra’s算法来计算从每个疏散地区到每个疏散点的最短路。
第三,分配避难点:通常政府机构会在安全区域设置避难点以应对灾害。考虑到每个疏散点的容量,若所有被疏散者都选择最近的目的地,则不能满足安置所有被疏散者的需求。因此,为了使总体的疏散距离最短,同时避免超出每个避难点的容量,利用避难点分配模型来分配来自不同区域的被疏散者到指定的避难点。在决定了疏散的目标疏散点后,根据选择最短路径的假设,抵达目的地的路径也会随之确定。
最后,疏散预警优化:在完成以上步骤之后,所有疏散预警模型的输入数据都已取得。此模型通过控制预警信息的传播以最大化被疏散人群的数量,输出是一个疏散预警的发布日程表,可以为政府的决策者提供发布预警消息的具体指导。
在实际疏散问题中,公众做出的疏散决策可看作一个有序的离散选择问题[9],因此疏散的需求和路网状况信息的动态变化一般是在一些离散的时间点发生。本研究在研究预警发布策略时加入了时间成分,将整个疏散过程划分成均匀的时段,在每个时段内将需求和路网信息看作是常量,而在不同时段则基于滚动时域[20]策略更新路网信息和公众决策,将动态问题转化为一系列离散时间点的静态决策问题。同时,各种预警发布渠道影响下的疏散响应率可由统计数据给出,或由需求模型计算而得,通常情况下其分布服从S曲线(S-Curve)[28]。
1.2 参数和变量设置
(1)设疏散网络G=(N′,A′)表示所研究地区的交通网络图。在这个网络中,N′,A′分别表示全部的点和线,但事实上网络是十分庞大的,并不需要考虑全部的点和线。因此,利用N,A来表示在疏散过程中用到的点和线。将点的集合N划分为三个子集,Nk是疏散地区的点的集合(k表示疏散点编号),Nd是疏散避难点的集合(d表示避难点编号),No是疏散路径的交点。A则表示交通网络中用于疏散的道路的集合(a表示路网中的道路编号)。另外,将疏散总时间划分为均匀的时段,T是疏散时间段集合(l∈T表示时间段编号);J是信息来源方式的集合(j⊂J表示信息来源组合方式编号),即可以在同一个时段通过不同的消息源组合的方式发布疏散预警信息。
(2)其他相关参数:Qd:避难点d的容量;rkd:从疏散点k到避难点d所需的出行时间;nk,t=2:在疏散开始时(t=1),在疏散点k需要被疏散的人数;pjkt:当在t时段k地区人群接收到从信息发布渠道方式j的预警信息时的疏散响应率;Cn:路网中道路a的容量;Bat:在t时段道路a上的背景交通流量;β:私家车去往避难点的比率;δak:描述从疏散点k出发,是否通过道路a的0-1向量,当道路a被使用时,其值为1,否则其值为0。
(3)变量:wkd:避难点分配决策变量,当疏散点k地区的群众分配给避难点d时,其值为1,否则其值为0;
xjkt:疏散预警信息发布方式的决策变量,在t时段向疏散点k通过j方式发布预警信息时,其值为1,否则其值为0;
nk,t≥z:在t时段初,疏散地区k还未疏散的人群数量(t≥2),此变量由t时段前已经疏散的人群数量决定。
1.3 避难点分配模型
将不同疏散地点的人群指派到不同的避难点,构建避难点分配模型,使总体的出行行程最短。
其中,式(1)的目标函数是从所有的疏散地区到避难点的总的行程时间最小。约束条件(2)是令到每个指定避难点的私家车疏散的人数不超过避难点提供给私家车的容量。约束(3)是确保每个疏散地区需分配给一个避难点。约束(4)定义了决策变量是0-1变量。此模型为整数线性规划模型,利用Gurobi软件的内置算法可以对模型进行有效计算。
1.4 疏散预警模型:
其中,目标函数(5)是使最终总的疏散人数最大化。约束(6)是使用每条路线的自行疏散的人群的数量不能超过道路的容量。约束(7)计算了属于疏散地区k的在下一个疏散时段的疏散人群(未被疏散的剩余人群)的人数。约束(8)在每个疏散的时段,不能有超过一种的方式来发布预警信息给在某个地区的特定类型的人群。约束(9)定义了决策变量是0-1类型。
2 模型的启发式算法
本文建立的应急避难点模型是线性模型,可使用分支定界法进行求解,本文采用科学计算软件Gurobi进行求解。而疏散预警发布模型中nk1是已知的,但当t≥2时,nkt是决策变量。因此模型(P)是非线性模型,因此不能直接通过优化软件求解,本文采用了一个贪婪的启发式算法进行求解。具体算法流程如下:
Setp1参数初始化:输入交通网络参数疏散网络相关参数G=(N′,A′),Nk,Nd,No,A,Qd,rkd,ca,Bat,β,nk,t=1,等初始数据,以及疏散预警模型参数(可调节),T,J,pjkt。
Setp2通过路网数据,运用Dijkstra’s算法计算从各个疏散点到避难点的最短路。
Setp3将数据及参数带入避难点分配模型,运用整数规划软件求得各疏散点指配的避难点,通过Step2中计算的最短路得到路网中的道路使用参数δak。
Setp4计算
计算此模型后,利用xjk1变量的值得到:

(14)

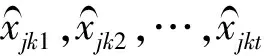
说明以上求解过程通过计算每个时段的最优解来求得全局的解,事实上并不能证明此方法可以得到全局最优解,因此,通过下节算例可以对此算法进行进一步分析,以证明方法的有效性和可行性。
3 模型的优化分析
3.1 单地区迭代过程的最优性
命题1本研究采用的贪婪启发式算法,在单地区多时段的问题中,可以得到最优解。
证明(1)设一个疏散地区在两个时段(T=2)内进行疏散,并且没有道路容量的限制。本研究提出的迭代的流程算法会使每个数段内的被疏散人数最多,即通过令第一时段疏散的人数Z1和第二时段被疏散的人数Z2分别最大化,可以使两时段内疏散总人数最多。根据疏散预警模型(P),则单地区两时段模型可化为:
maxZ=Z1+Z2
(15)

(16)
xjt∈{0,1},∀j∈J,t∈T
(17)

(18)

(21)

(22)
若存在式(22),那么任何大于或等于第一时段的疏散比率将会导致同等或更多的总体疏散比率。证明如下,重新变换公式(22),得到:

(23)

(24)

(25)

(2)设一个疏散地区在三个时段(T=3)内进行疏散的例子,其他条件不变,模型表示如下:

(26)

(27)
xjt⊂{0,1},∀j⊂J,t⊂T
(28)

(29)

(36)
根据式(32),可以得到三个阶段被疏散人群的总数:
(38)

(3)运用归纳法可以推断出在单地区单类别被疏散群体并且不考虑阻塞条件时,需要在每个时段最大化被疏散人群的数量来使总体的被疏散人数最多。这也是这个启发式算法迭代过程所解决的问题。
3.2 多地区算例中的反例
设两个被疏散地区,两个时段,以及两种预警发布源的算例。两种信息发布源可以构成四种发布信息的方式(J=0,1,2,3分别代表发布源:无消息发布,发布源1,发布源2,发布源1与2同时发布消息)。这两个被疏散的地区公用同一条道路进行疏散,道路容量为(Ct),则有:

(39)
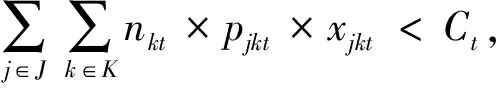
(40)

(41)
xjkt⊂{0,1},∀j⊂J,k⊂K,t⊂T
(42)

(43)
在这个算例中,所有的输入参数设置如下:
在开始阶段(t=1),在不同的地区(nkt)需要被疏散的人口数量分别为:n11-100,n21-200;不同时间的道路容量(Ct):C2-75,C2-80;不同的预警发布源方式在不同时间发布消息会导致疏散的概率:p111=0.15;p211=0.2;p311=0.3;p112=0.5;p212=0.6;p312=0.7;p121=0.15;p221=0.2;p321=0.3;p122=0.5;p222=0.6;p322=0.7。
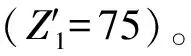
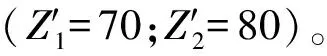
说明虽然此算例表明本研究所用的方法求得的解可能并非最优解,但是算例中所设置的条件属于“特殊情况”,在实际生活中,发生类似情况的概率极低。例如,在多地区两时段情况下,这种特殊情况需要满足至少以下两个条件:第一,运用本算法求得在后时段的疏散人数的最大值要远远小于道路的容量,且其差值要足够大;第二,后一个时段的疏散响应比率要远大于第一个时段。只有同时满足这两个条件才可能存在更优于本算法的解。但是,实际生活中这两个条件基本不可能同时满足,因此可以推断,本算法在实际条件下可求得最优解。
3.3 贪婪启发式算法
以文献[29]中算例的疏散网络为例说明模型的应用,设某沿海区域即将遭受自然灾害的侵害,需在T=5个时段(每时段3小时,共15小时)内疏散危险区域人群。疏散网络如图1所示,此区域有D=2(D1,D2)个避难所需要安置疏散群众的车辆以应对灾害的避难点,共有K=3(K1,K2,K3)个疏散点人员需要被疏散,其余顶点代表弧交叉点No,边上的第一个数字为相应弧在一个时段内的最大容量,第二个数字为通过弧所需要的旅行时间。初始各个疏散点的人数:K1处20个单位,K2处30个单位,K3处25个单位。各个避难点容量:V1,V2处均为50个单位。

图1 疏散网络图
应用本研究设计的启发式算法进行求解。
首先,参数初始化:输入交通网络参数疏散网络相关参数G=(N′,A′),Nk,Na,No,A等如图1所示,其中Ca-Bat,rkd分别为图中边上的第一和第二个数值;Qd和nk,t=1分别为避难点容量(Q1=Q2=50)和疏散点人数(n11-20,n11-30,n31=25);其他参数,T=5,I=3,β=1,pjkt值的设定见表1,这里pjkt设置成固定的参数值,且不区分地区差异,但在实际应用中,可以根据具体情况,在每个时段更新参数的动态信息。

表1 算例中疏散响应率pjkt值的设定
运用Dijkstra’s算法计算从各个疏散点到避难点的最短路,将数据及参数带入避难点分配模型,运用整数规划软件Gurobi求得各疏散点指配的避难点,通过计算的最短路得到路网中的道路使用参数δak,各疏散点分配的避难点及指定的路径如表2所示。

表2 各疏散点到指定避难点的路径
将得到的δak及其他初始参数值代入到疏散预警模型(P1)求解,并利用本研究设计的贪婪启发式算法结合Python编程,使调用Gurobi内置算法对算例进行了T次的迭代运算,得到疏散预警模型结果如表3所示,即通过不同渠道发布预警消息给特定地区的时间表(预警策略)。

表3 疏散预警发布方案
表3表示的是在5个时段内,算例中的3个地区应该采用哪种方式发布信息。其中,j=0,1,2,3分别代表发布源:无消息发布,发布源1,发布源2,发布源1与2同时发布消息。则通过疏散预警模型计算出的发布策略为:在第一时段从信息发布源2发布消息到疏散点K1,发布源1与2同时发布消息到疏散点K2和K3;在第二时段信息发布源2发布消息到疏散点K1,发布源1发布消息到疏散点K2,而在疏散点K3不发布任何消息;在第三时段从信息发布源1与2同时发布消息到疏散点K1和K2,在疏散点K3仍不发布任何消息;在第四时段从信息发布源1与2同时发布消息到所有疏散点;在最后时段仍发布所有预警消息到所有疏散点。由此可以观察出,在前三个时段,信息发布的策略各不相同,以此来减少道路中的堵塞情况,而在后两个时段,由于未被疏散的人数的减少,道路可以承载剩余人在特定时间内撤离,因此需要尽可能的发布所有消息,动员剩余公众的撤离。
通过进一步分析得到此疏散策略可以达到的疏散率如图2所示,其中曲线All标记了三个疏散点的总人口疏散比率可以达到90%以上,而K1和K2两个疏散地区的人口几乎全部撤离,而K3地区由于在第二和第三时段不发布预警,因此有一段时间疏散比率不变。曲线的形状与设置的pjkt的参数值有关,由于本算例中的疏散响应率的设置不区分地区,只区分时间,所以各地区疏散率走势基本一致。而其中K1和K3两个疏散地区在算例中共享某几段疏散道路(如表2所示),因此呈现较大差异。

图2 累积疏散率
3.4 模拟退火优化算法
模拟退火算法最初由Kirkpatrick提出[30],通常被用来在优化问题中寻求一个全局最优解。本研究中,虽然迭代的启发式算法能够求得局部最优解,为了确认其是否为全局最优解,笔者尝试利用模拟退火算法来优化从迭代算法中获得的解。具体的算法流程如下:
Step0初始化:设s=0,iteration=0;设定初始温度Tems,降温系数α,利用Gurobi内置算法求得的初始可行解WScurrent,即预警策略集X{xikt|xjkt=1},并计算预警策略得到的最优目标函数值f(WScurrent)。
Step1邻域搜索:根据当前解WScurrent,生成其领域解WSnew,并计算f(WSnew),令iteration-iteration+1。

Step3若iteration Step4若满足终止准则,则停止搜索,得到最优解WScurrent;否则设iteration=0,s=s+1,降温Tems+1=α×Tems,并转到Step 1。 在Step 0的初始可行解是由本研究提出的启发式迭代算法求得。为了搜索到新的可行解(预警方案),在模拟退火算法的Step 1中,随机选取一个时段t,并且获得了这个时段的预警方案。然后,随机选取其中一个有效解(xjkt=1),并设置其值为0;根据式(8),由于选择的有效解即决策变量值为1,则其他此时段其他解的值则为0(即选择一种方式对特定地区发布预警);所以随机选择此时段同地区值为0的解,并将该解的值进行0-1互换,进而得到一个新的策略集,记为WSnew,检查新的策略集的可行性。 为验证本研究提出的贪婪启发式算法的有效性,利用以上步骤对上节算例进行进一步计算。其中,模拟退火算法的参数设置为初始温度Tems=100,降温系数α=0.95,迭代次数iterationmax=50,外循环终止温度阈值Tems=1,初始可行解WScurrent为利用迭代线性规划的启发式算法得到的解(小结3.3.1)。通过利用Python编程以及Gurobi优化程序应用模拟退火算法不断修改参数计算,尽管进行了大量的测试,并未找到比初始解更优的解。说明了本研究所设计的依据时间过程迭代的贪婪启发式算法已近乎求得全局最优解。这与本研究的结论相一致,除“特殊情况外”,迭代的贪婪启发式算法可以求得最优解,并用于解决实际问题。 本研究为自然灾害预警提供了一个信息发布方式的研究框架,解释了更有策略的发布预警消息可以使疏散更有效率,建立了避难点分配和多时段疏散预警模型,设计了适用于模型的迭代启发式算法。本研究的结果提供了在疏散的不同时段选择哪种的预警信息发布源来发布预警消息的日程表,为良好的风险沟通及制定相应的应急疏散预案提供理论支持。整个模型框架在算例分析中应用三个不同算例,明确了算法的适用范围,表明了这个方法可以得到单地区疏散的最优解,多地区除“特殊情况”也可得到最优解,且运用模拟退火算法并不能使解优化,说明本算法可以得到合理且有意义的结果,并可以用来在现实的疏散过程中通知公众完善应急疏散预案。另外,这个模型框架也可以应用在其他地区,在求解过程中,算法的迭代过程为各个时段间的联系提供了更新信息的接口,可以依据实际情况调整参数的变化,即通过实时信息更新疏散响应率,道路容量等参数信息,有较强的灵活性。 本研究的假设存在一定局限性,第一,疏散地区的公众是无差别的进行疏散,第二,目的地均为避难点。下一步的研究可以依据公众的特点,将其划分为不同类别进行分别探讨,发现其疏散响应的规律,进一步将模型细分,还可增加关于疏散目的地选择模型,使研究更加的完整。4 结论
