有砟轨道与无砟轨道动刚度特性差异研究

2019-07-10成都工业职业技术学院轨道交通学院成都608西南交通大学高速铁路

铁道标准设计 2019年7期

亓伟，闫雪，曹勇 (.成都工业职业技术学院轨道交通学院，成都 608；.西南交通大学高速铁路

线路工程教育部重点实验室，成都 610031)

1 概述

有砟-无砟轨道过渡段是高速铁路两种不同轨道间设置的不得已的工程过渡措施。随着行车速度的不断提高，高频段荷载所占比重增加，对线路动态平顺性提出了更高要求，其中动刚度是保证线路平顺性的重要指标[1-4]。为保证列车在更高速度下安全、平稳地通过有砟-无砟轨道过渡段，首先需要研究有砟轨道与无砟轨道间的动刚度特性差异。

动刚度是不同激振频率的荷载作用下轨道抵抗变形的能力，是轨道系统各层结构动响应的叠加，它反映的是全频段系统振动与轨道各结构层振动的关系[5-7]。随着我国列车运行速度不断提高，对线路基础的平顺性提出了更高要求，因此需要对轨道的动刚度特性展开研究，而轨道动刚度主要与系统组成结构与所受激振荷载有关。

有砟轨道与无砟轨道是目前我国高速铁路的两种主要轨道结构形式，为保证高速列车行车平稳性，需要对两种轨道的动刚度展开研究。由于两种轨道结构组成差异较大，而线路中存在较多有砟-无砟轨道过渡段，为保证高速列车在所有线路的平稳运行，因此需要重点研究两种轨道间的动刚度差异。目前仅文献[4，5]对有砟轨道的动刚度特性作了研究，指出高速行车下轨道动刚度研究的重要性。但是现在依然缺少对于无砟轨道动刚度、两种轨道间动刚度特性差异的研究。同时，现有轨道过渡段的设置措施有扣件刚度过渡、道床刚度过渡、轨枕过渡、辅助轨过渡等措施[8-13]，但这些措施主要是实现两种轨道间静刚度的过渡，对于两种轨道间动刚度过渡缺乏研究。

随着行车速度的不断提高，高频段荷载所占比例逐渐增大。我国高速铁路现已达到350 km/h，并提出研制400，600 km/h的超高速列车的计划，高频段荷载的增加使得动刚度差异研究变得尤为重要。以车速为120 km/h与600 km/h的德国低干扰普、美国六级谱与我国高速铁路谱下的轨道高低功率谱密度作对比[14]，如图1所示。由图1可知，随着行车速度的提高，3种轨道谱下的高频段荷载所占比例大幅提高。以我国高速铁路谱为例，激振荷载频率为2 000 Hz时，车速120 km/h下的轨道高低功率谱密度为3.34×10-10m2/(rad/m)，而当车速提高至600 km/h，轨道高低功率谱密度增加至7.48×10-8m2/(rad/m)，相同频率下高频段列车荷载提高了224倍。同样的，车速为600 km/h时，中国高速铁路谱在2 000 Hz时的高低功率谱密度与车速为120 km/h时，400 Hz时的中国高速铁路高低功率谱密度相同。由此可知，在行车速度较低时，线路设计按静刚度设置是合理的，但随着行车速度的不断提高，高频段荷载所占比例的增加，需要对轨道动刚度展开研究，尤其是过渡段处动刚度的过渡研究。

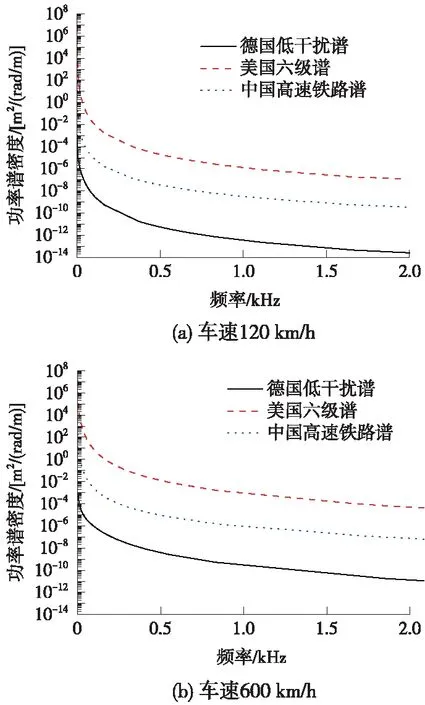
图1 不同行车速度时各激振频率对应的高低不平顺功率谱密度

国内外专家学者已对线路病害尤其是过渡段病害问题作了大量研究，现有线路动力学研究中，通常是建立车辆-轨道耦合动力学模型分析线路病害对行车的影响及对轨道结构受力的影响；现场的大量测试内容以车辆通过病害治理地段的车辆振动特性、轨道受力情况为主[15-21]。但是，这些研究忽略了特定频率下车辆、轨道结构的振动特性，而随着行车速度提高，轨道动刚度问题变得越发突出后，尤其是共振频率附近的轨道动刚度特性，因此需要对车辆、轨道结构在不同频率下的动刚度特性展开研究。有砟轨道与无砟轨道动刚度特性对于高速行车的平稳性、工务养护维修中特定波长不平顺的消除及将来开展过渡段动刚度过渡的研究均有重要指导作用，但目前缺乏轨道动刚度特性相关研究工作，为此本文对两种轨道的动刚度特性及其差异展开深入研究。

2 力学模型

有砟轨道与无砟轨道两种轨道结构组成差异较大，本文以桥上有砟轨道与桥上双块式无砟轨道为例建立相应的力学模型，研究两者间的动刚度差异，两种轨道的力学模型如图2、图3所示。

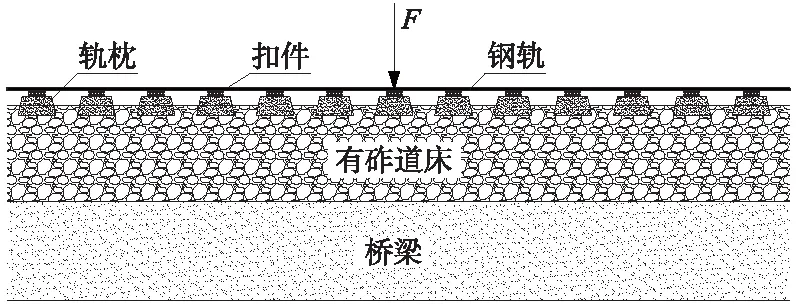
图2 桥上有砟轨道力学模型

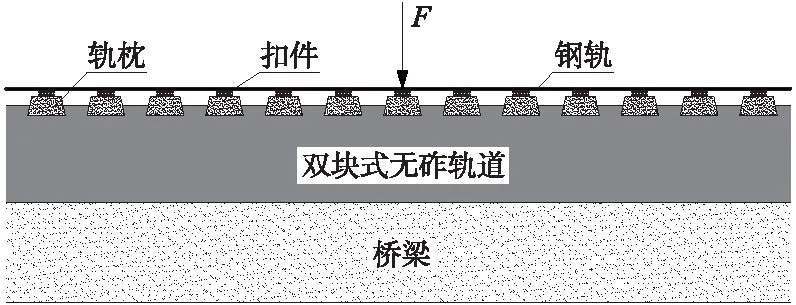
图3 桥上双块式无砟轨道力学模型

2.1 模型简化

结合轨道部件自身特点及其在动刚度特性中的表现情况，适当简化建立的有砟轨道与无砟轨道的力学模型，轨道各部件在力学模型中的具体简化情况如下。

钢轨采用CN60钢轨，无砟轨道扣件间距0.65 m，有砟轨道扣件间距0.6 m。扣件系统简化为起传力与减振作用的刚度-阻尼弹簧，有砟轨道扣件静刚度取60 kN/mm，无砟轨道扣件静刚度取25 kN/mm，两种扣件阻尼均为75 kN·s/m。有砟轨道采用IIIA型有挡肩轨枕，简化为梁结构，划分为0.2 m的单元。双块式无砟轨道的轨枕块与现浇道床板粘结为一个整体，模型中将其与道床板作为整体结构分析。有砟道床简化为离散质量块与刚度-阻尼弹簧，有砟轨道的道床具体参数见表1。桥上双块式无砟轨道简化为一个钢筋混凝土整体结构，无砟轨道道床参数见表2。桥梁简化为长32 m，截面惯性矩7.65 m4的实体模型，网格划分与道床相同。桥梁采用 C50 混凝土，弹性模量为3.45×104MPa，混凝土密度采用2 500 kg/m3。模型中其他参数参考文献[14，19，22]。

表1 IIIA型轨枕有砟轨道相关参数

表2 双块式无砟轨道相关参数

2.2 边界与约束条件

为消除动荷载作用下边界效应对动刚度的影响，有砟轨道与无砟轨道均选取50跨轨枕长度(即有砟轨道30 m，无砟轨道32.5 m)。通过分析两种轨道在静荷载、各共振频率下的钢轨加速度纵向传递规律，如图4、图5可知，模型选取50跨轨枕是可行的。

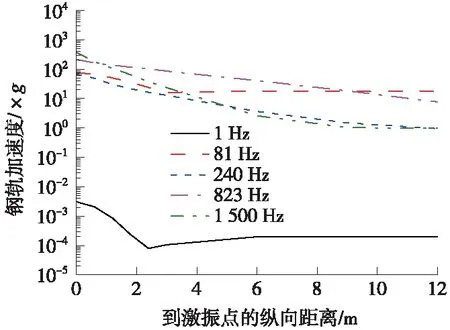
图4 有砟轨道钢轨加速度的纵向传递规律

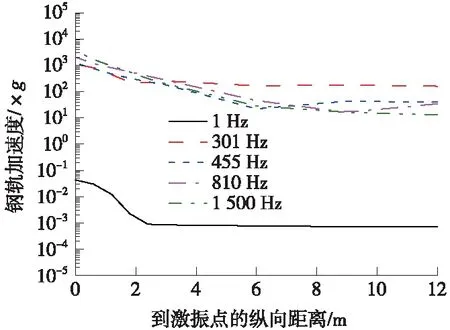
图5 无砟轨道钢轨加速度的纵向传递规律

模型中钢轨两端限制x方向(沿线路方向)的位移，沿z方向(线路横向)的位移以及绕x轴和y轴的转动。有砟轨道的轨枕在列车荷载作用下主要承受上部钢轨传递的竖向荷载，因此模型中的轨枕限制其x方向、z方向位移，限制其绕y轴的转动。有砟轨道的道床简化为质量块与刚度阻尼弹簧，其3个方向均有弹簧连接，因此质量块不施加约束。无砟轨道的道床在其4个端部分别施加纵、横向位移的约束。桥梁底部两端全约束。

2.3 荷载取值

轨道结构在简谐荷载的激励下产生的振动方程

(1)

由此可得相应的动刚度

(2)

式中F(iω)——作用在轨道部件上的节点力；

u(iω)——轨道部件的相对位移。

有砟轨道与无砟轨道扣件刚度与道床组成差异较大，因此，在研究两者间的轨道动刚度差异时，需要分别分析轨道动刚度与轨下动刚度两部分。轨道动刚度即动荷载作用于钢轨上，对应各频段的轨道抵抗变形的情况，它可以反映轮轨间的振动特性，便于分析车辆振动、钢轨振动情况。轨下动刚度是指动荷载作用于不包含钢轨的轨下部件时，轨道轨下各部件的动刚度情况，它可以反映轨道部件的振动情况，这有利于分析轨道部件可靠性、稳定性。

由前文已知，轨道动刚度特性分为轨道动刚度与轨下动刚度两部分，因此模型中的荷载施加分别为施加于钢轨上与扣件上。为研究有砟轨道、无砟轨道的动刚度特性差异，荷载分别加载于有砟轨道中段、无砟轨道中段。

分析轨道动刚度时，施加的荷载F=F0eiωt，F0为列车静轴重，ω激振频率。参考文献[4]，F0=15 kN，ω=1～2 000 Hz。

3 结果分析

3.1 轨道动刚度差异

有砟轨道与无砟轨道的轨道动刚度对比如图6所示，根据两种轨道的动刚度特性差异，可以将其划分为低、中、高频三部分。低频段为低于50 Hz段，该部分振动主要影响乘车舒适性、轨道结构疲劳寿命等；中频段50～500 Hz，该频段主要为轨道结构共振频段及轮轨振动频段；高频段500～2 000 Hz主要是轮轨高频振动及噪声的来源。

图6 有砟轨道与无砟轨道动刚度对比

对比有砟轨道与无砟轨道的轨道动刚度低频段可知，随激振频率的增加轨道动刚度变化较小，整个低频段轨道动刚度与轨道静刚度量值相近，有砟轨道动刚度略低于96 kN/mm，无砟轨道动刚度略低于70 kN/mm。对比有砟轨道与无砟轨道的动刚度可知，随激振频率的增大，有砟轨道动刚度略有降低，无砟轨道动刚度略有增大。由于无砟轨道扣件刚度低于有砟轨道扣件刚度，低频段无砟轨道的动刚度均低于有砟轨道的动刚度。由此可知，列车由一种轨道驶入另一种轨道时，轨道结构动刚度必然存在过渡变化问题，当该频段轨道动刚度出现较大的交替变化时会影响乘车舒适性和轨道结构寿命，因此有砟-无砟轨道过渡段的设置需要实现低频段轨道动刚度的均匀过渡。

对比中频段有砟轨道与无砟轨道的轨道动刚度可知，轨道动刚度变化趋势受轨道共振频率影响较大，共振频率处轨道动刚度出现明显的极小值。有砟轨道的第一共振频率与无砟轨道的第一共振频率差异显著，有砟轨道的第一共振频率为81 Hz，此时轨道动刚度为24.8 kN/mm，无砟轨道的第一共振频率为240 Hz，此时的轨道动刚度为228 kN/mm。第一共振频率下无砟轨道动刚度衰减显著低于有砟轨道，有砟轨道动刚度不足轨道静刚度的26%，无砟轨道第一共振频率时的动刚度是轨道静刚度的3.5倍。无砟轨道在第一共振频率后，轨道动刚度随激振频率的增加整体呈增长趋势，而有砟轨道仍在189 Hz时出现第二共振频率轨道刚度的衰减情况。中频段两种轨道间动刚度差异显著且存在显著的共振情况，因此有砟-无砟轨道过渡段设置时应保证两种轨道结构动刚度的过渡问题。

对比高频段有砟轨道与无砟轨道的轨道动刚度可知，随激振频率的增加，有砟轨道与无砟轨道动刚度均逐渐增大，且两种轨道的动刚度已经非常接近，相同频率下无砟轨道动刚度略大于有砟轨道的动刚度。高频段两种轨道间动刚度差异较小，表明高频段轨道动刚度情况受轨下刚度差异较小，且两者均达到静刚度的5倍以上，可以保证轨道结构稳定性，因此有砟-无砟轨道过渡段设置中可以减少高频段动刚度过渡的研究。

此外，为维持线路动态稳定性，需要注意控制线路共振频率范围内的激振荷载。由此可知，无砟轨道应重点控制激振频率为240 Hz的线路高低不平顺，即350 km/h的无砟轨道客专应控制波长为0.4 m的高低不平顺，而600 km/h的无砟轨道客专应控制波长为0.7 m的高低不平顺。有砟轨道应重点控制激振频率为81，189 Hz的线路高低不平顺，即350 km/h的有砟轨道客专应控制波长为1.2，0.51 m的高低不平顺，而600 km/h的有砟轨道客专应控制波长为2.1，0.88 m的高低不平顺。

3.2 轨下动刚度差异

轨下动刚度为轨道钢轨以下的轨下结构在动荷载作用下的动力特性，有砟轨道与无砟轨道的轨下动刚度对比如图7所示。同样可以将轨下动刚度分为低、中、高频段三部分进行分析。

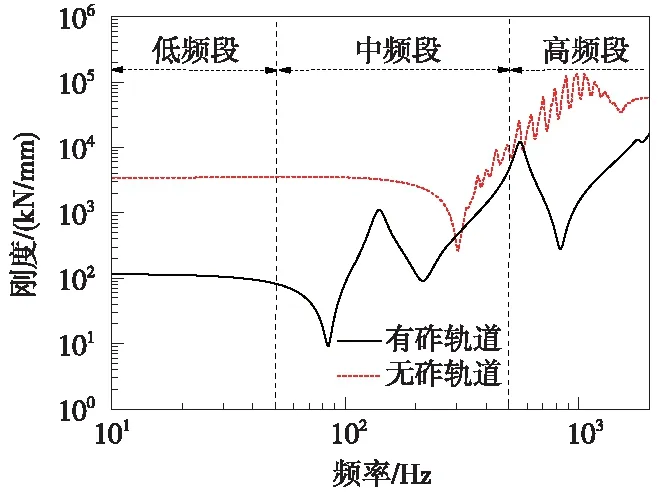
图7 有砟轨道与无砟轨道轨下动刚度对比

在低频段，随激振频率的增加，两种轨道的轨下动刚度均出现小幅降低趋势。但由于无砟轨道道床板整体刚度远大于有砟轨道道床刚度，低频段的有砟轨道轨下动刚度远低于无砟轨道的轨下动刚度，相同激振频率下无砟轨道的轨下动刚度达到有砟轨道的30倍以上。由此可知，列车荷载由一种轨道驶入另一种轨道时由于两种轨道的轨下动刚度差异过大，会增加两种轨道结构低频段的振动情况，进而会增加两种轨道结构的疲劳伤损问题，有砟-无砟轨道过渡段的设置需要实现两种轨道的轨下动刚度均匀过渡的目的。

对比中频段有砟轨道与无砟轨道的轨下动刚度可知，无砟轨道轨下动刚度整体大于有砟轨道轨下动刚度，轨下动刚度变化趋势受轨道共振频率影响较大，共振频率处轨下动刚度出现明显的极小值。有砟轨道的轨下动刚度第一共振频率与无砟轨道的第一共振频率差异显著，有砟轨道第一共振频率为84 Hz，无砟轨道第一共振频率为303 Hz。第一共振频率下无砟轨道的轨下动刚度衰减显著，且低于同频率下的有砟轨道轨下动刚度，此时无砟轨道轨下动刚度仅为256 kN/mm，不足其静刚度的1/15。有砟轨道的轨下刚度在第一共振频率时仅为9.1 kN/mm，不足其静刚度的1/13。此外，有砟轨道在214 Hz时存在第二共振频率，此时的轨下动刚度为91 kN/mm，略低于轨下静刚度。无砟轨道第一共振频率后，有砟轨道第二共振频率后，两种轨道的轨下动刚度随激振频率的增加逐渐增大。中频段两种轨道轨下动刚度的差异除共振频率时，差异随激振频率的增加逐渐减小。对比共振频率下两种轨道的轨下动刚度情况可知，共振频率对两种轨道的轨下动刚度影响显著，此时轨道结构稳定性急剧下降，因此需要尽量减少该频段的激振荷载。但是，列车由一种轨道驶入另一种轨道时，激振频率发生变化会对两种轨道的轨下动刚度造成影响，因此有砟-无砟轨道过渡段的设置需要尽可能减少中频段，尤其是轨下刚度出现共振频率的频段激振荷载出现波动。

对比高频段有砟轨道与无砟轨道的轨下动刚度可知，两种轨道的轨下动刚度特性出现较大差异。有砟轨道在560 Hz时轨下动刚度达到一个极大值，之后随激振频率增加轨下动刚度逐渐减小，在830 Hz时出现第三共振频率，此时轨下动刚度为278 kN/mm，已达到其静刚度的2倍以上。之后随激振频率的增加，有砟轨道的轨下动刚度逐渐增大。而无砟轨道的轨下动刚度随激振频率的增加出现波动增加的情况，这是由于无砟轨道的道床板是实体单元，网格的划分使得无砟轨道轨下刚度在高频段存在较多的共振频率，但是高频段的无砟轨道轨下动刚度已达到其静刚度的5倍以上，可以保证轨道结构的稳定性，共振频率对其影响已较小。高频段有砟轨道的轨下动刚度随激振频率的增加与无砟轨道的轨下动刚度差异逐渐增大，但此时两种轨道的轨下动刚度均可以保证轨道的稳定性，因此，有砟-无砟轨道过渡段的设置中可以减少对高频段轨下动刚度过渡的研究工作。

通过分析有砟轨道与无砟轨道的轨下动刚度特性可知，两者在全频段均存在较大差异。随着列车速度的不断提高，中高频段的荷载所占的功率谱密度逐渐增加，有砟轨道与无砟轨道间的轨下动刚度差异问题变得越发严重，因此，有砟-无砟轨道过渡段的设计需要着重考虑轨下动刚度过渡的要求。此外，通过分析有砟轨道与无砟轨道的轨下动刚度特性可知，无砟轨道应重点控制激振频率为303 Hz的线路高低不平顺，即350 km/h的无砟轨道客专应控制波长为0.32 m的高低不平顺，而600 km/h的无砟轨道客专应控制波长为0.55 m的高低不平顺。有砟轨道应重点控制激振频率为84，214 Hz的线路高低不平顺，即350 km/h的有砟轨道客专应控制波长为1.16，0.45 m的高低不平顺，而600 km/h的有砟轨道客专应控制波长为1.98，0.78 m的高低不平顺。