基于量表得分的最小临床重要性差值(MCID)制定方法*

薛红红 杨 铮 万崇华△ 许清安 许传志 陈 莹

20世纪20年代，问卷测量作为一种新的测评工具在国外兴起，随后在医学领域得到广泛的应用。问卷测量结果是一个综合性的指标，相较于临床客观指标能够更全面、多维度地反映出被调查者的综合健康状态。但由于问卷测量结果的大小常常反映被调查者主观感受，缺乏客观性，问卷测量差异具有统计学意义并不代表在临床上也有实际的意义。越来越多的学者认识到仅根据治疗前后量表得分差异的假设检验P值来判断疗效是不科学的，只要样本例数足够大，P值一般都会显示统计学意义，但并不能说明有临床意义。因此，量表应用中的一个关键问题是得分要改变多少才具有临床意义。1987年，最小临床重要性差值(minimal clinically important differences，MCID)的概念首次被提出，随后加拿大学者Jaeschke R等人对其进行定义，认为MCID是在不考虑副作用和成本的前提下，被病人认可的最小问卷维度得分变化值[1-2]。以不同的角度最小临床重要性差值主要可分为三类。以Jaeschke R、Guyatt等人为主的最小显著变化值(minimal important difference,MID)，强调MID是可观察到的最小的变化，无论被调查者是改善还是恶化[3-5]；其二是最小可测变化值(smallest detectable difference,SDD,也记作minimal detectable change,MDC)：指在一定置信度的前提下，结合评价工具测量误差所确定的最小可测变化；其三是充分重要变化值(sufficient important difference,SID)：其主要目的是为克服最小临床意义变化值的不足,指在考虑成本和副作用后确定的病人最小受益值。

MICD是统计和临床建立关系的桥梁，其重要性不言而喻。如何制定合理可信的MCID值成为学者研究的热点。传统方法主要有2种，包括效标法(anchor-based methods)，又称锚法，以及分布法(distribution-based methods)。传统方法虽有其优势，但尚无统一的标准，在使用过程中其缺点与局限性也逐渐暴露出来。近年来，不断有新的方法被提出，如：基于锚的MIC分配法、线性回归模型和logistic回归模型等。本文将对已有方法尤其是近年来新出现的方法如何应用进行较详细的介绍，为量表(问卷)MCID的制定等问题提供依据和参考，并通过住院系统性红斑狼疮患者实例分析，比较不同方法下MCID值的大小。

MCID制定方法及步骤

1.效标法(锚法)

效标法是由1993年美国学者Lydick等人提出，又名锚法，其原理是通过检验量表与另一独立测量工具评分或其他指标的关系来阐明该量表评分改变的含义。可分为2个步骤：首先选择一个恰当的锚并报告锚与检验量表的相关系数；其次计算干预前后在锚选项上至少相差一个等级的患者的问卷得分差值，若差值服从正态分布，则以差值的均值作为MCID，若差值服从偏态分布，则以其中位数为MCID[6]。

锚的性质可分为客观锚和主观锚(又可分为患者和专家评价2种类型)。锚的种类有横断面锚和纵向锚。横断面锚与时间无关，一般用于完全随机设计；纵向锚与时间有关，一般适用于自身配对设计或重复测量设计。以锚为基础的方法关键是要寻找适宜的锚。没有很好的锚时，可以在测定的问卷中另外加入一个或几个特定的条目，并以此作为总体评价的一个标准(锚)，调查锚得分变化与所测量得分变化的关系。

2.分布法

分布法是根据观察到的评分变化分布情况估计MCID，其分布变异情况可以采用几个效应统计指标，有明确的计算公式并将测量误差纳入计算。如标准差(SD)、效应尺度(ES)、测量标准误(SEM)、标准化反应均数(SRM)等[7-10]。当不能用锚法时，可采用分布法。分布法的MCID计算公式及指标见表1。

3.基于锚的MIC分配法(anchor-based MIC distribution)

2007年de Vet HC等[11]借助ROC曲线提出了可视化的基于锚的MIC分配方法。其核心在于选择一个恰当的锚并以其为分类的金标准，以干预前后被调查者问卷评分的改变值作为试验分类方法，寻找灵敏度与特异度都最佳的改变值作为MCID(MIC)。应用的具体步骤如下：

表1 分布法指标汇总

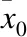
(1)基于锚分组：以SF-36中条目q1为锚，若患者治疗后相较于治疗前在锚问题的选项上正向改变至少一个等级，则归为“改善组”。若患者治疗前后在锚问题的选项上未改变，则归为“无变化组”。若患者治疗后相较于治疗前在锚问题的答案上反向改变至少一个等级，则归为“恶化组”。根据患者治疗前后在锚条目的选项上的变化情况对其进行归类，称为锚分组。

(2)分布图绘制：计算3种不同分类中被调查者两次问卷测量分数的变化值(dchange)，并分别绘制dchange的频率分布图(以百分数表示)。

(3)明确研究目的：若要制定最小临床重要性改善值，将“无变化”组分布图的95%上限值定义为有较大改善值(MIC)，其计算公式：MIC=Meanchange+1.645SDchange。(注：95%上限值在ROC曲线中特异度为95%；1.645对应5%面积(单侧))。

(4)ROC曲线的构建：以无变化组分布图的最小值与95%上限值为取值范围，确定组距、截断点。以的锚分组为金标准，以不同截断点分别为试验分类方法，计算每个截断点的灵敏度和1-特异度。1-特异度为横坐标，灵敏度为纵坐标进行描点，形成ROC曲线。

(5)选择ROC曲线中最左上角的点(Youden指数最大的点)作为截断点值，即为最佳分类阈值(MIC值)。

4.响应累计分布函数(cumulative distribution function of responses,CDF)

2013年Wyrwich等[12]代表国际生命质量研究会ISOQOL顾问委员会推荐了利用响应累计分布函数CDF来制定MCID。如图1为一条累积分布曲线图，累积分布函数能完整描述一个实随机变量X的概率分布。若以X轴为干预前后问卷得分的变化值(dchange)，从左到右依次增大，Y轴为概率值，对任意变化值x，累积分布函数定义为F(x)=P(Xx)，即x对应的y值等于所有小于等于x的值出现概率之和。

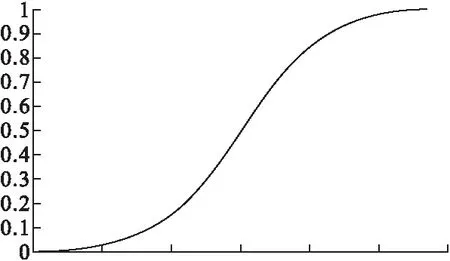
图1 累积分布曲线图

2018年Cheryl等人[13]在文献中，表明响应值的定义是能够识别被调查者干预前后临床结果评估(COA)变化值中有意义的变化值。响应值的确定方法有：基于锚的经验累积分布函数、判别分析、锚法。响应累积分布函数制定MCID应满足：(1)一个合理的研究设计(锚与COA同时使用)；(2)至少选择一个恰当的锚(锚与COA的结构必须一致)；(3)报告锚与临床结果评估(COA)变化值的相关系数r。

5.多元线性回归模型法

2017年Angst等[14]提出了借助多元线性回归模型制定MCID的方法，可以调整潜在的混杂因素；其原理是以干预前后被调查问卷得分改变量(dchange)为因变量，以年龄、性别、基线得分、组别等混杂因素为自变量，对dchange拟合多元线性回归模型，对配对纵向队列研究其多元回归模型的具体构建步骤如下：

(1)分组：若患者治疗后相较于治疗前在过渡问题的选项上正向改变至少一个等级，则归为“改善组”。若患者治疗前后在过渡问题的选项上未改变，则归为“无变化组”。若患者治疗后相较于治疗前在过渡问题的答案上反向改变至少一个等级，则归为“恶化组”[15-16]。

(2)确定研究对象组：例如过渡问题“今天(随访时)与基线相比，你的健康状况如何”，其选项为：1.好了很多，2.好了一些，3.没变化，4.差了一些，5.差了很多。若要制定最小临床重要改善值，则以选择“好了一些”和“没变化”这两组患者为研究对象。

(3)模型构建：对分组因素进行赋值(例：没变化=0、好了一些=1)，以组别、性别、年龄、基线等混杂因素为自变量，以“dchange”为因变量，构建多元线性回归模型。

(4)MCID值：采用SPSS软件构建多元线性回归模型并输出其预测值的均值，预测值的均值即为最小临床重要改善值，也可计算其95%可信区间。

6.其他方法

除上述方法外，还可以采取专家意见法和文献分析法来制定MCID。专家意见法是根据专家的意见来确定最小临床意义变化值,常用技术是Delphi法。因其依赖专家的主观判断,不能较好地反映病人的观点。Brozek等认为在确定以病人为主的最小临床意义变化值时，专家意见法只能作为辅助。根据已有文献，Revicki等将meta分析作为确定最小临床意义变化值的一种方法，他们认为临床试验证据的不断积累为确定最小临床意义最小值提供丰富的、有价值的信息。文献分析法依赖于已有文献,在确定最小临床意义变化值时只能起辅助作用[17,7]。也有一些学者探讨了几种方法结合制定MCID。如选择多个锚计算其均值，也可见以计算分步法中不同指标下的MCID值，再求其均值等方法。表2对已有方法的优缺点及使用环境进行了总结。

表2 常见MCID制定方法基本特征

通过上述总结，可以看出锚法与分布法作为广泛使用的方法，不限研究的设计类型。分布法有好几种指标且易受样本量的影响，不同的指标又有不同的参数可选。本研究采用了一个实例(详见实例分析中的表3)，探讨以锚为参照，观察分布法中各种方法对应MCID的变化，结论为：当找不到合适的效标时，建议首选分布法中1.96SEM法或SRM=0.8时对应的MCID，其次考虑ES(0.5)法。

实例分析

1.对象资料

本研究是对已有的研究数据为实例进行分析。已有数据来源于自身配对的实验设计，以昆明医科大学第一附属医院住院系统性红斑狼疮患者为研究对象，采用系统性红斑狼疮患者生命质量量表QLICD-SLE(V2.0)、SF-36中条目(总的来讲您的健康状况是：1.非常好；2.很好；3.好；4.一般；5.差)为锚，对住院系统性红斑狼疮患者进行三次调查，分别在患者入院当天、入院第二天、干预后出院前一天。QLICD-SLE(V2.0)量表包含生理、心理、社会功能、疾病特征四个领域，共计47个条目。x0表示被调查者的基线评分(入院当天)，x1表示被调查者干预后评分(出院前一天)，d为同一个患者两次测量得分标准化后的差值。

2.结果

(1)基本情况

研究共计调查系统性红斑狼疮患者143例；其中女性132例(92.3%)、男性11例(7.7%)；患者的年龄主要集中在30～40岁，约占40%；回收有效问卷102例(71.3%)。PROISCD-SLE V1.0量表的重测信度系数r为0.903，锚得分(第一次)与患者基线得分的相关系数0.43。由于d值为患者两次问卷评分差值(X1-X0)，既有正值也有负值，其标准差是9.96，均数是1.16。调查对象中有70例患者在干预前后在锚条目的选项上的结果未发生变化，其对应的量表得分差值的均值为0.36，标准差为8.32。被调查者第一次问卷评分的均数是67.6，标准差是13.27；第三次问卷评分的均数是68.8，标准差是12.67。

(2)MCID值

通过不同的方法得出的MCID值具体结果见表3。其中ES、SRM、RS均以0.2为小效应，0.5为中等效应，0.8为大效应[18]。基于锚的MIC分布法MCID值对应的敏感度0.63，特异度为0.66。通过比较分布法中不同指标下MCID值与锚法对应的MCID值，可看出SEM法中X=1.96时对应的MCID值与SRM=0.8时最为接近。SEM法中X=1时的MCID(4.11)与ROC曲线法中的4.26最为接近。当ES=0.5对应的MCID值(6.63)与多元线性回归(6.71)以及锚法(6.69)最为接近。

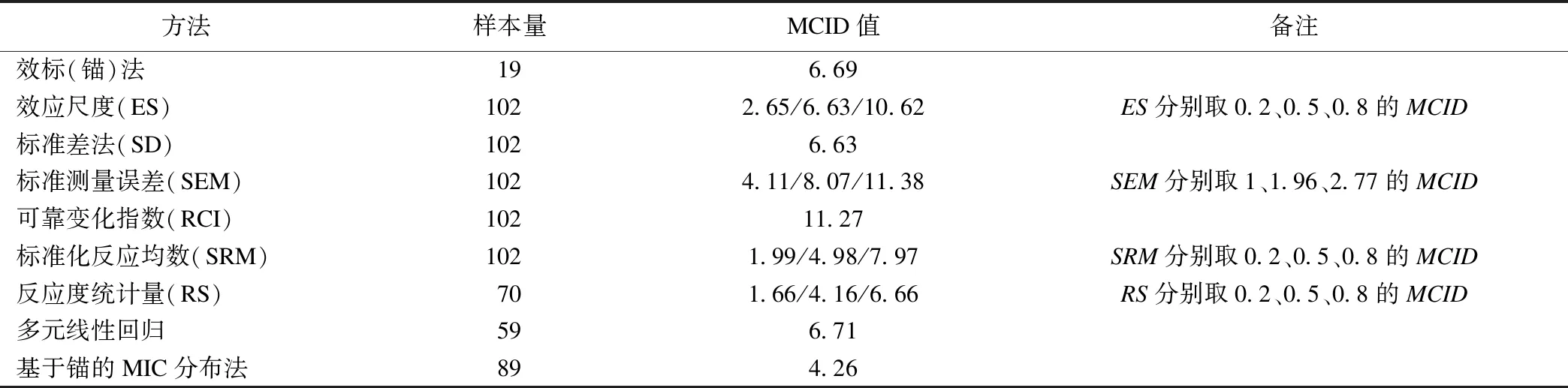
表3 不同方法的MCID值

讨 论

根据国内外文献[19-32]在慢性病领域中，常选用传统方法中的锚法、分布法制定MCID值。锚法中常见以SF-36、圣乔治呼吸问卷(SGRQ)等国际公认的综合量表为锚；也可见选用两种锚，求其均值作为MCID。分布法是用统计学的指标估计MCID值，常用于自身配对的实验设计或治疗组和对照组在某一时间点或更多时间点的比较。也可见综合锚法与分布法，取其最大值、最小值，最终以最大值与最小值和的均值作为MCID，以减小统计误差[33-34]。2017年Angst等人将统计中P值得概念引入MCID计算中，得出ES、SRM更适用于配对设计资料，ES的取值在0.3～0.5之间，可用于MCID的粗略估计[8]。我国学者许清安等人[35]采用SPSS模拟的手段，分析了ES法、SEM法、RCI法的应用条件并对其适用范围提出了建议。本文通过自身配对的实例分析，发现锚法与1.96SEM法得出的MCID最为接近，建议当找不到合适锚的情况下，首选1.96SEM法或SRM为0.8时对应的MCID值，其次考虑ES(0.5)法。

近年来在方法学研究上，以研究最小临床重要性改善值为主；基于锚的MIC分配法利用ROC曲线制定MCID相较于传统的方法使其灵敏度、特异度可视化，而且具有较好的稳定性[8]，适用范围较广；Turner等[36]通过一个实例表明，利用整个队列的数据与ROC曲线制定MCID能有效提高MCID准确性。在纵向队列研究中多元线性回归模型能够有效控制混杂因素对MCID的影响，并且能够识别出对MCID影响最大的混杂因素[11]。响应累积分布函数制定MCID作为一种新的方法已被学者对其理论概况进行探讨，但未见实例报道。

如今MCID如何体现出个体差异成为人们关注的热点。2010年Henrica等人[37]提出ROC曲线法计算的MCID的95%可信区间等方法可用来量化其用于单个患者时的不确定性。2013年Linda等[38]提出以置信区间估计MCID的范围时，如果置信区间跨入由MCID定义的临床无差异区域，则无法建立治疗方案对结果的影响(正面或负面)，不能只依靠值或95%CI计算MCID的取值范围，必须结合临床实际情况得出合理的结论。