轮廓爆破孔壁压力峰值计算方法*

2019-07-10叶志伟卢文波

爆炸与冲击 2019年6期

陈明，刘涛，叶志伟，卢文波，严鹏

（1. 武汉大学水资源与水电工程科学国家重点实验室，湖北武汉 430072；2. 武汉大学水工岩石力学教育部重点实验室，湖北武汉 430072）

轮廓爆破是岩体开挖成型及爆破损伤控制的主要手段，被广泛应用于水利水电、交通及矿山等工程建设领域。作用在爆破孔孔壁的爆炸荷载压力峰值，直接影响到岩体轮廓成型质量及其保留岩体的损伤破坏范围，是进行轮廓爆破参数设计及非流固耦合爆破振动响应数值模拟分析的关键参数之一，受到了爆破工程技术研究人员的高度关注。

传统的轮廓爆破均采用不耦合装药结构，众多研究者分析了不耦合装药条件下爆破荷载峰值。朱瑞赓等[1]、费鸿禄等[2]较早研究了不耦合装药炮孔内的峰值压力计算方法；王志亮等[3]运用数值模拟对水不耦合炮孔的孔壁压力进行了研究，揭示了炮孔中压力的变化规律；凌伟明[4]利用试验方法研究了炮孔壁的峰值压力；王伟等[5]根据爆轰产物中反射波方程和介质中的冲击波方程求解出岩体中爆炸冲击波参数，并与弹性波理论透射公式结果对比，发现两者间的差别很大；刘云川等[6]指出了现有孔壁压力峰值计算方法可能存在的不足，并按照能量等效的原则，提出了炮孔压力峰值的计算公式；Feldgun 等[7]利用数值模拟方法研究了爆破荷载的变化过程，数值模拟结果与理论及试验结果非常一致。其他学者[8-10]也研究了炮孔的压力峰值问题，并考虑了轴向装药系数的影响，提出了各种不同形式的计算公式。总体上，由于爆破孔内炸药的爆轰过程、爆炸冲击波与炮孔壁相互作用的复杂性以及爆炸荷载测试技术的局限性，难以直接测量出孔壁压力峰值，而且计算值与实测值的差别也较大：炮孔孔壁压力峰值的问题一直吸引着众多学者的关注。

目前最常用的轮廓爆破孔壁压力峰值计算方法有2 种。

第1 种常用方法，基于爆生气体的膨胀过程计算。在工程误差允许范围内，将爆生气体的膨胀过程分为等熵膨胀和绝热膨胀2 个阶段[11]，且考虑爆生气体与炮孔壁的相互作用。爆炸压力大于炸药临界压力的阶段，按等熵膨胀分析；爆炸压力小于炸药临界压力的阶段，按绝热膨胀计算。

若装药不耦合系数较小，则爆生气体的膨胀只有等熵膨胀状态，孔壁的压力峰值：

若装药不耦合系数较大，爆生气体的膨胀需经历等熵膨胀和绝热膨胀2 个阶段，孔壁的压力峰值：

式中： pr为孔壁压力峰值； pw为平均爆轰压力，为装药直径；db为炮孔直径；db/dc为装药不耦合系数；ρe为炸药密度；D 为炸药爆速；k、γ 为绝热指数，通常取为冲击波碰撞压力增大倍数，n=8～11，一般取n=8；为炸药的临界压力，一般中等威力炸药取为200 MPa。

第2 种常用方法，基于临近炮孔壁的空气冲击波特性计算。其计算方法：

这2 种方法都包含冲击波碰撞压力增大倍数n，n 取值的大小对孔壁压力峰值的影响最显著。方法1中n 取值变化范围较小；方法2 认为n 随着入射压力的变化而变化。实际上，由于爆炸空气冲击波与炮孔壁相互作用的复杂性，比较合理地确定n 值的大小仍有难度，导致轮廓爆破孔壁压力峰值难以准确确定。

综上所述，目前关于轮廓爆破孔壁压力峰值问题仍有待进一步研究，本文采用理论与数值模拟相结合的方法，研究了空气冲击波与爆破孔孔壁相互作用后，爆破孔壁上的压力与空气冲击波强度之间的关系，建议了一种新的轮廓爆破孔壁压力峰值计算方法。

1 空气冲击波与孔壁的相互作用

由于炮孔为圆柱形，炸药爆炸时炮孔内的空气冲击波作用过程复杂，并存在透、反射的叠加效应。为便于研究，简化爆破孔壁与空气冲击波的作用界面为一平面，并假定爆破孔壁处于弹性状态，此时将炮孔壁简化为图1 所示的弹性界面F-F，设入射波I 从介质Ⅰ传播到另一种声阻抗不同的介质Ⅱ中，传播方向垂直于界面，即讨论正入射的情况。当入射波扰动到达界面时，不论对于第一种介质而言，还是对于第2 种介质而言，都引起了一个扰动，即分别向2 种介质中传播反射波扰动R 和透射波扰动T[13]。

下面从理论上推求分析空气冲击波与弹性壁的相互作用。

图 1 冲击波反射和折射示意图Fig. 1 Schematic diagram for shock wave reflection and refraction

冲击波自左向右传播如图1 所示，设 p0、 ρ0、 v0为入射介质初始压力、密度和质点速度； p1、 ρ1、 v1为冲击波波后参数， c1为入射冲击波波速度； p2、 ρ2、 v2、 c2为反射波波后参数； p3、 ρ3、 v3、 c3为透射波波后参数；p30、 ρ30、 v30为透射初始参数。

间断面上的冲击波质量、动量、能量守恒关系式就是冲击波的基本关系式[14]：

式中：c 为冲击波速度；p、ρ、v 和e 分别为介质的压力、密度、速度和比内能，带下标“0”的量表示波前参数。

多方气体状态方程为[14]：

式中：τ 为比容，γ 为绝热指数。

按照动量守恒定律，冲击波传播过程中，单位时间内作用于介质的冲量等于其动量的变化，对透射波则有[14]：

由式(8)中 p300， v300可得：

假定两介质界面始终保持接触，于是根据牛顿第三定律，界面两侧质点根据应力连续条件得到[15]：

冲击波在岩石中迅速衰减为弹性应力波，并以恒速传播，对于大多数岩石来说，冲击波作用范围很小，可忽略不计， c3可近似为岩石纵波波速 c30。由式(9)可推得：

联立式(4)～(7)、(10)～11)求解可得：

其中：

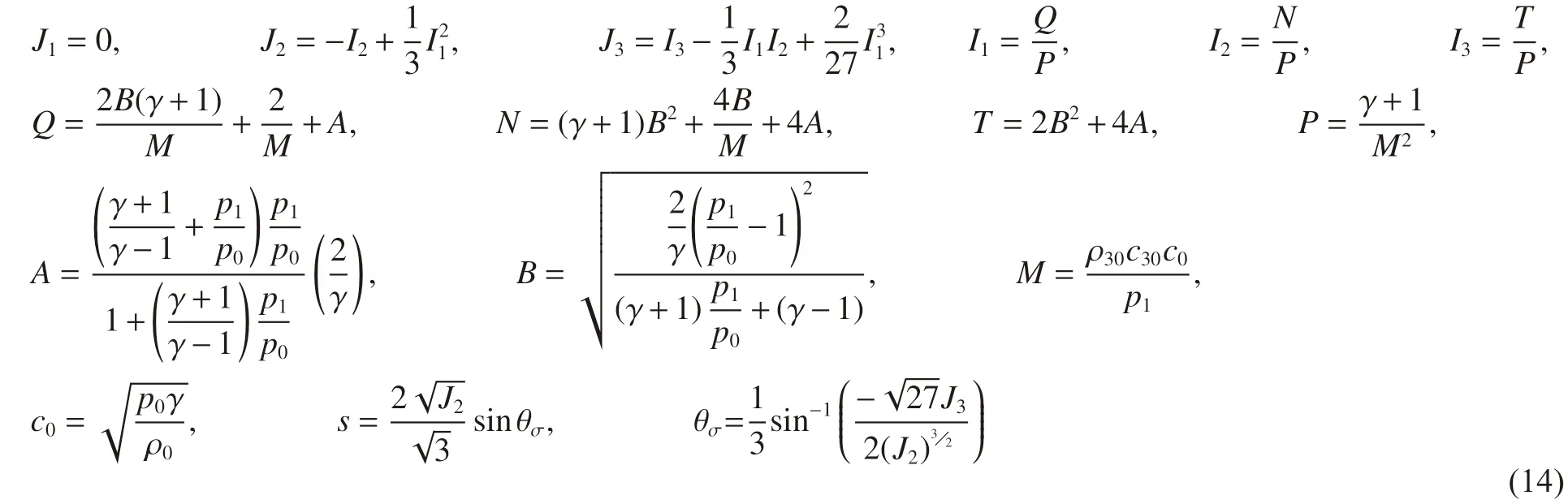
式中： c0为入射波波前气体声速。

为探寻压力增大倍数n 的影响因素，图2 给出了不同绝热指数条件下，绝热指数γ 分别取为1.2 和

图 2 不同入射压力下p3/p1 与介质波阻抗的关系Fig. 2 Relationship between p3/p1 and wave impedance of transmission medium at different incident pressures

上述研究中，将炮孔壁简化为平面状态，忽略了反射冲击波因炮孔壁实际上的弧面特征可引起的二次冲击波斜碰撞进一步增大炮孔壁近区的压力，可能导致理论推导的n 值较实际的增大倍数偏小。下面采用流固耦合数值分析方法，模拟分析常用的传统轮廓爆破参数条件下的炮孔壁压力峰值。

2 轮廓爆破孔壁压力峰值的数值模拟

本数值计算中采用LS-DYNA 的流-固耦合任意拉格朗日-欧拉(arbitrary Lagrangian-Eulerian，ALE)算法模拟炸药的冲击作用，其中炸药、空气采用Eulerian 算法，岩石、堵塞采用Lagrange 算法，其原理是实现材料在网格中流动，可有效计算爆炸冲击过程中的大变形问题。

2.1 计算工况

为进一步研究轮廓爆破孔壁压力峰值与周围介质条件、不耦合系数、炸药性能的关系，基于实际工程中常见的工程岩体特性、爆破参数及炸药类型，选择粉砂岩、石灰岩、花岗岩3 种岩体分别代表软岩、硬岩及坚硬岩类炮孔介质，选择装药直径与炮孔直径比分别为25/42、25/50、32/76、32/90、32/110 的5 种常用轮廓爆破不耦合装药结构，选用乳化炸药、多孔粒状铵油炸药2 种炸药展开研究。为研究轴向不耦合装药结构时炮孔壁的压力峰值状况，继续建立了轴向装药系数分别为0.6 和0.3 的对比数值模型，轴向装药系数为装药长度与炮孔药室长度的比值。

2.2 计算模型

因模型具有对称性，采取1/4 模型，如图3 所示，尺寸为1.5 m×1.5 m×3.0 m，其中堵塞长度为0.5 m，装药长度为1.5 m，孔底岩石长度为1.0 m，为能模拟出炸药的真实爆炸效果以及确保不同工况结果之间具有可比性，模型炸药和空气单元的尺寸控制在2 mm 以内，岩石单元尺寸也和炸药、空气单元尺寸相近，不同装药条件下控制模型单元尺寸相同，不同介质条件，不同炸药种类作用时保证模型网格一致，所建立的统一模型的单元数量约为38 万，节点数量约为40 万。同时计算的时间步也要和模型最小单元尺寸相匹配，以便观察到冲击波与孔壁的透反射效果。为控制模型边界的影响，计算模型中的人工截断边界分别设置为无反射边界和对称边界，如图3 所示。

2.3 计算参数

粉砂岩、石灰岩、花岗岩3 种岩石材料选用常用的双线性随动硬化塑性模型，并根据Cowper-Symonds 计算式考虑应变率对岩石动态强度的影响[16]，参照《岩石力学参数手册》[17]，各种岩石的参数取值见表1。

炸药选用M A T_H I G H_E X P L O S I V E_BURN 材料模型，并结合JWL 状态方程模拟炸药爆炸过程中压力与体积的关系：

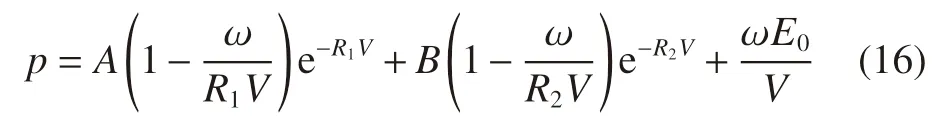
式中：p 为JWL 状态方程决定的压力，V 为相对体积，E0为初始比内能，A、B、R1、R2和ω为描述JWL 方程的独立常数。以上参数的取值方法均参考LS-DYNA 用户手册[16]。乳化炸药、多孔粒状铵油炸药的相关参数取值详见表2。

空气材料模型采用线性多项式状态方程，空气压力计算公式：

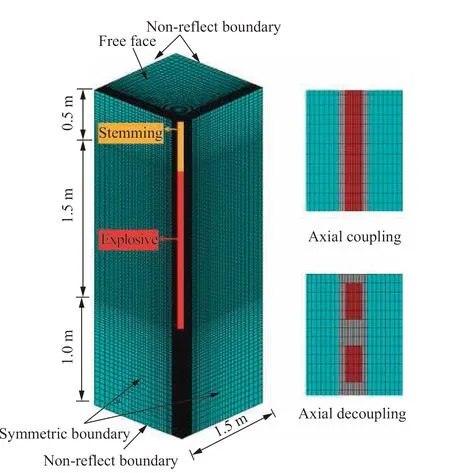
图 3 计算模型示意图Fig. 3 Sketch of calculational model

式中：C0=C1=C2=C3=C6=0，C4=C5=0.4，μ=ρ/ρ0，ρ、ρ0分别为初始材料密度和当前材料密度，e 为比内能。

表 1 岩石物理力学参数Table 1 Physical and mechanical parameters of rock

表 2 炸药相关参数Table 2 Parameters of explosive

2.4 模拟结果分析

图4 给出了部分典型工况下空气冲击波与孔壁作用的压力时程曲线。从图4 可以看出压力时程曲线有一个明显的拐点，空气冲击波与孔壁作用后压力有一个显著的提高，拐点前最大压力为入射压力p1，拐点后最大压力为反射压力p2，孔壁处径向应力为透射压力p3即孔壁压力峰值。表3、表4 分别给出模拟反射压力p2、透射压力p3与入射压力p1的比值，图5、图6 分别给出了相对应的曲线。表5 给出了径向不耦合装药时数值模拟与常用方法1、2 理论计算得出的孔壁压力峰值；表6 给出了径向与轴向均不耦合装药时，装药系数分别为0.6 和0.3 的炮孔壁单元的最大径向应力的平均值，以及装药系数为1.0 时孔壁压力峰值，分析径向和轴向不耦合装药系数对孔壁压力峰值的影响。

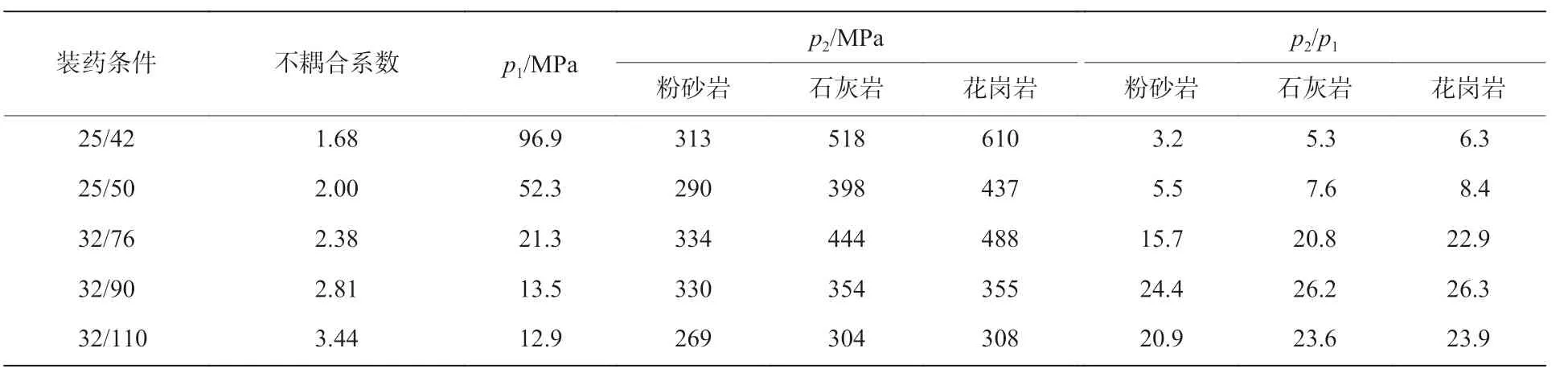
表 3 乳化炸药作用下空气冲击波反射压力与入射压力比值Table 3 Ratio between reflected pressure and incident pressure of air blast wave induced by emulsion explosive

表 4 乳化炸药作用下空气冲击波透射压力与入射压力比值Table 4 Ratio between transmission pressure and incident pressure of air blast wave induced by emulsion explosive

图 5 乳化炸药作用下空气冲击波反射压力与入射压力比值Fig. 5 Ratio between reflected pressure and incident pressure of air blast wave induced by emulsion explosive

图 6 乳化炸药作用下空气冲击波透射压力与入射压力比值Fig. 6 Ratio between transmission pressure and incident pressure of air blast wave induced by emulsion explosive

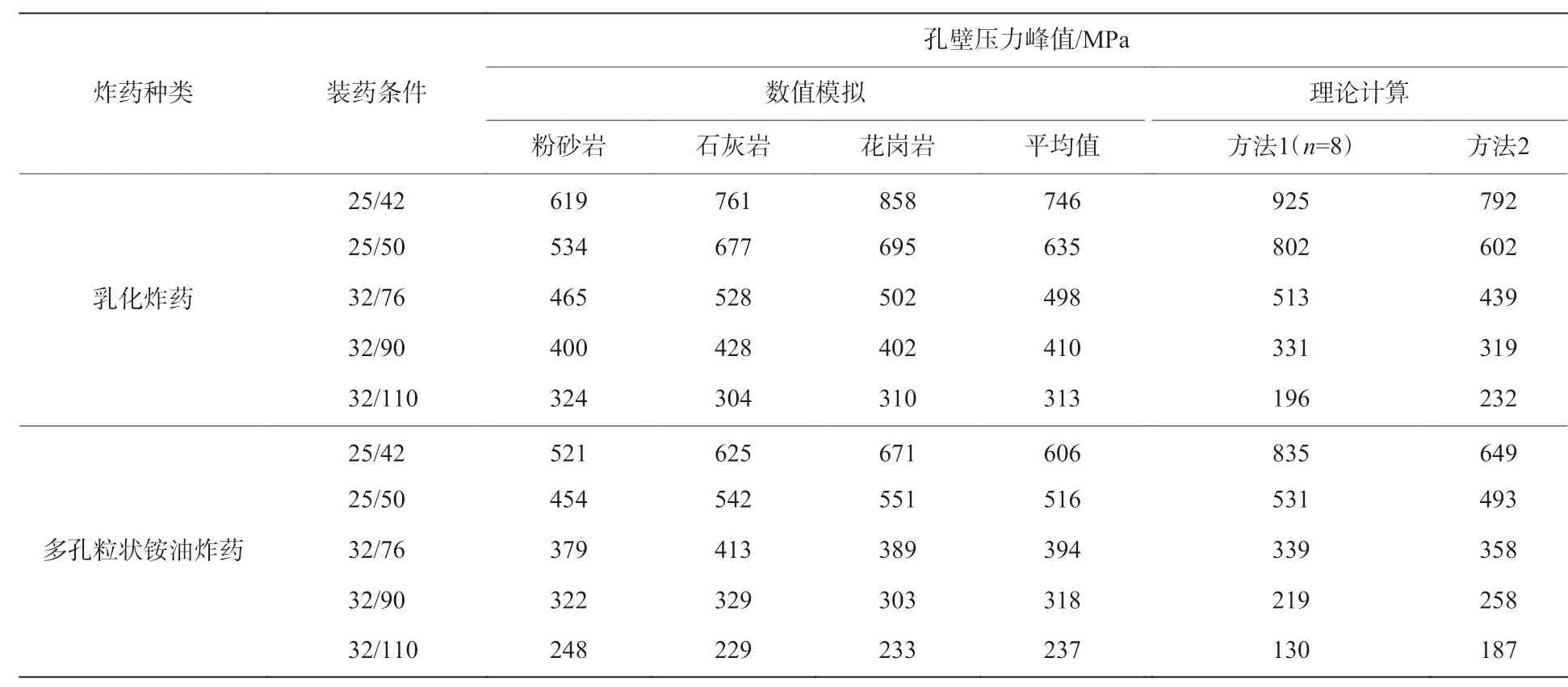
表 5 模拟与理论计算孔壁压力峰值对比Table 5 Comparison of borehole peak pressure between simulation and theoretical calculation

由表3～5、图5～6 可知冲击波的反射、透射压力增大倍数均与不耦合系数、透射介质波阻抗有关，而不是一个固定不变的值，不耦合系数影响尤其明显，当不耦合系数到2.81 以后，冲击波反射、透射压力增大倍数都会有一个下降的过程，这是因为当考虑炮孔壁的曲面特征及爆轰波的柱面特征时，不耦合系数大到一定程度后，冲击波在炮孔的透、反射的叠加效果开始减小。虽然不同透射介质空气冲击波透射压力与入射压力的比值不同，但是可以发现粉砂岩、石灰岩、花岗岩3 种介质条件的透射压力与入射压力比值差别并不大，这与图2 给出的结论一致。表6 中给出的不同装药条件下的孔壁压力结果表明，轴向装药系数分别为0.6 和0.3 时的平均压力值与轴向耦合装药时压力峰值的0.6 和0.3 倍大致相等，说明轴向不耦合装药的孔壁压力平均值与轴向装药系数密切相关，近似成正比关系。

表 6 不同装药条件下的孔壁压力峰值Table 6 Borehole peak pressure under different charge conditions

3 轮廓爆破孔壁压力峰值的确定方法

由上述分析可知，不耦合系数、被爆介质波阻抗、炸药性能等因素是影响轮廓爆破孔壁压力峰值的关键参数，从表5 中不同方法计算得到的结果对比也可看出，不同方法得到的结果差别较大；不耦合系数较大时，常用计算方法1 和方法2 的结果均明显偏小，而且已有主要方法也较少考虑轴向装药系数的影响。因此有必要寻找一种较准确又较简单方便的爆破孔壁峰值压力计算方法。本文中根据理论分析及数值模拟结果，基于3 种数值模拟中爆破介质条件孔壁压力峰值的平均值，研究轮廓爆破孔壁压力峰值计算方法。

传统的轮廓爆破，径向不耦合系数一般都大于1.5，爆生气体的膨胀过程有等熵膨胀和绝热膨胀2 个阶段，因此以爆生气体在炮孔中完成等熵和绝热膨胀时的压力为入射压力，数值模拟的透射压力为孔壁压力峰值，定义压力增大倍数，得到不同不耦合系数时的压力增大倍数见表7，将表7 的数值按炸药种类分类绘成压力增大倍数n´的曲线见图7。